Определение комплексных чисел. Алгебраическая форма комплексного числа.

Расширение понятия числа.

В современной математике, а также в ряде разделов физики и техники кроме действительных чисел используются числа более общей природы, которые называются комплексными числами. Комплексные числа имеют разные интерпретации: алгебраическую, геометрическую, электротехническую и др. В истории развития математики комплексные числа первоначально возникли в связи с решением алгебраических уравнений. Известно, что не всякое квадратное, или кубическое уравнение имеет решения в области действительных чисел. Например, уравнение х²+1=0 не имеет решений, так как на множестве действительных чисел не существует числа, квадрат которого равнялся бы отрицательному числу. Таким образом, для расширения понятия действительного числа необходимо ввести новое число, которое будет корнем уравнения х²+1=0. Традиционно такое число обозначается символом і.

Множество комплексных чисел должно включать множество действительных чисел. В пространстве комплексных чисел должны быть определены действия сложения и умножения, которые подчиняются обыкновенным законам алгебры.

Определение комплексных чисел. Алгебраическая форма комплексного числа.

Комплексным числом называется выражение а+bi, где а, b – действительные числа, а і – некий символ.

Множество комплексных чисел обозначается буквой С.

Запись комплексного числа в виде:

z=а+bi (1)

называют алгебраической формой комплексного числа. Причем а – действительная часть комплексного числа Re(z), а bi – мнимая часть комплексного числа Im(z).

Два комплексных числа считаются равными, если они имеют равные действительные и мнимые части.

В комплексном числе мнимая единица і определяется равенством: і² = -1.

Любое действительное число можно записать в виде комплексного числа:

z=а+0i .

если а = 0, то комплексное число становится чисто мнимым z =bi.

Два комплексных числа вида: z=а+bi и z =а-bi называются комплексно сопряженными.

Условились комплексное число z=а+bi отображать точкой плоскости с координатами (а;b) . Действительные числа изображаются точками оси абсцисс, которую называют действительной осью, а чисто мнимые числа – точками оси ординат, которую называют мнимой осью. Каждому комплексному числу z=а+bi соответствует точка на плоскости с координатами (а;b) , или радиус вектор, начало которого лежит в начале координат, а конец в точке (а;b) .

Модулем комплексного числа называется длина соответствующего ему вектора. Модуль комплексного числа z обозначается ІzІ и часто модуль обозначают буквой r.

Значение модуля вычисляют по теореме Пифагора по формуле:

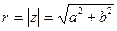. (2)

Если модуль равен некоторому положительному числу, то по определению модуля имеют место утверждения:

- множество всех чисел :z, для которых ІzІ= r, является окружностью с радиусом r и центром в начале координат;

- множество всех чисел :z, для которых ІzІ≤ r, является круг с радиусом r і центром в начале координат;

- множество всех чисел :z, для которых ІzІ › r, является дополнение (внешние точки) окружности радиусом r и центром в начале координат.

3.. Действия над комплексными числами в алгебраической форме

Пусть заданы комплексные числа : 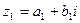и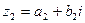

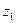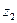Суммой чисел и называется число:

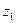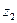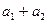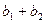+ =( )+( )і (3)

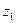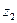Произведением чисел и называется число:

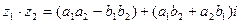(4)

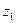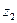Частным чисел и называется число:

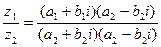(5)

Для комплексных чисел выполняется коммутативный и ассоциативный закон для сложения, а также коммутативный, ассоциативный и дистрибутивный законы для умножения.

Приведем примеры решения упражнений:

1) найти сумму и произведение комплексных чисел 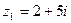и .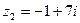

Решение:

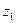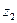+ =(2-1)+(5+7)і=1+12і;

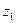
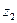=(2+5і)(-1+7і)=-2+14і-5і+35і²=-2+9і-35=-37+9і;

2) решить уравнение:

х²-4х+13=0.

Решение:

D=16-52=-36, заменим -1 на і², тогда : .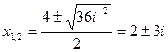

3) найти частное комплексных чисел 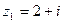та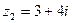

Решение:

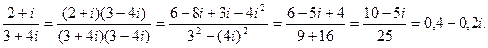
4) вычислить: і³

Решение:

і³= і²∙і = (-1)∙і =-і.

Задания для закрепления и самоконтроля:

1) Решить уравнение: 5х²+6х+5=0. Ответ: .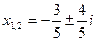

2) Вычислить сумму, разность, произведение комплексных чисел:

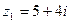та 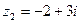. Ответ: 3+7і; 7+і; -22+7і;

3) Вычислить 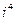. Ответ:1.

4) Найти частное комплексных чисел: (-1+6і); (2+5і).

Ответ: 28/37 – 17/37 і.

5) Изобразить комплексные числа в системе координат и показать их суммарный вектор: (-2+і); (3+3і).

Контрольные вопросы.

1. Что называется комплексным числом?

2. Какие существуют формы записи комплексных чисел?

3. Что называют мнимой единицей?

4. Какие действия можно выполнять над комплексными числами, заданными в алгебраической форме?

5. Чем отличается действительная часть комплексного числа от мнимой?

6. Как изобразить комплексное число на плоскости?

7. Дать геометрическую интерпретацию суммы и разности комплексных чисел.

8. Изобразить на плоскости комплексные числа: -2і; 6+3і; 4; -3-5і; 2-і.

9. Как найти сумму двух комплексных чисел?

10. Как вычислить произведение комплексных чисел?

11. Какие числа называются комплексно-сопряженными?

12. Как вычислить частное комплексных чисел?

13. Как решить квадратное уравнение с отрицательным дискриминантом?

Литература:

И.И..Валуцэ, Г.Д.Дилигул «Математика для техникумов», М.,1989, ст.78-95.

ЛЕКЦИЯ № 15

Модуль 2. Комплексные числа.

Тема: Тригонометрическая форма комплексного числа.

Цели: ознакомить с понятием аргумента комплексного числа, рассмотреть правила действий над комплексными числами в тригонометрической форме.

План.

1. Аргумент комплексного числа.

2. Тригонометрическая форма комплексного числа.

3. Действия над комплексными числами в тригонометрической форме