Основные положения конвективного теплообмена

Конвективный теплообмен представляет собой совместный процесс конвекции и теплопроводности. В технологических системах процесс обмена тепловой энергией между потоком жидкости и газа и твердым телом может протекать в двух направлениях:

- теплота передается от твердого тела в жидкость или газ – от инструмента в охлаждающую среду, от подшипника в охлаждающее масло и т. д.;

- теплота передается от жидкости или газа в твердое тело – при нагреве плазменной дугой или газовой горелкой, охлаждение масла в гидробаке и т.д.

Конвекция может быть естественной, когда элементы технологической системы отдают теплоту в неподвижный (спокойный) воздух или жидкость. Конвекция может быть вынужденной, когда твердое тело обменивается теплотой с жидкостью или газом, которые принудительно движутся (от насоса или вентилятора). Вынужденная конвекция происходит и в том случае, если тело перемещается в окружающей среде. Оба вида конвекции – естественная и вынужденная – как правило, происходят одновременно, т.е. в одной зоне конвекция вынужденная, в другой – естественная.

Процесс конвективного теплообмена описывается законом Ньютона- Рихмана.

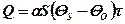(Дж), (5.1)

где Q – количество теплоты, предаваемой при теплообмене, Дж;

α – коэффициент теплоотдачи, ;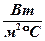

S – площадь поверхности, на которой происходит теплообмен, м²;

Θ_S и Θ_O – температуры поверхности и среды;

τ – время теплообмена, с.

Плотность теплового потока, проходящего в жидкость или газ

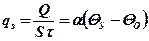(Вт/м²) (5.2)

Коэффициент теплоотдачи α может быть определен в результате решения дифференциального уравнения, полученного из закона Фурье (формула 1.9)

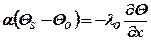, (5.3)

где λ₀ – коэффициент теплопроводности среды, ;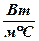

х – ось системы координат с началом на поверхности теплообмена, направленная вглубь жидкости.

Аналитическое решение дифференциального уравнения (5.3) может быть получено только для простых случаев, как правило, далеких от реальных условий теплообмена. Поэтому на практике для решения задач конвективного теплообмена используют численные методы решения; а также экспериментальные данные. В результате расчетов и на основе экспериментальных данных получено критериальное уравнение конвективного теплообмена.

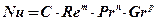(5.4)

В этом уравнении

Nu – безразмерный критерий Нуссельта;

C – коэффициент;

Re – безразмерный критерий Рейнольдса;

Pr – безразмерный критерий Прандтля;

Gr – безразмерный критерий Грасгофа;

m, n, p – показатели степеней.

Критерий Нуссельта равен

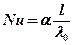, (5.5)

где α – среднее значение коэффициента теплоотдачи

на поверхности Вт/м²°С;

λ₀ – коэффициент теплопроводности среды, Вт/м·°С;

l – характерный размер тела, м.

Характерный размер определяется следующим образом:

- для плит и пластин – размер по направлению движения среды;

- для цилиндров и валов при обтекании поперек оси – диаметры;

- для других некруглых тел – эквивалентный диаметр

,

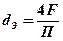F – площадь поперечного сечения тела,

П – периметр этого сечения.

Критерий Рейнольдса определяется по формуле

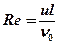, (5.6)

где u – скорость потока среды, м/с;

ν₀ – кинематическая вязкость среды, м²/с;

l – характерный размер тела, м.

Безразмерный критерий Прандтля

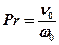, (5.7)

где ω₀ – коэффициент температуропроводности среды, м²/с.

Критерий Грасгофа определяется из выражения

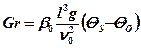, (5.8)

где β₀ – коэффициент объемного расширения среды, 1/°С;

g = 9,81 м/с² – ускорение силы тяжести.

Значения теплофизических характеристик среды λ₀, ν₀, β₀ существенно зависят от температуры. Поэтому в расчетах необходимо установить при какой определяющей температуре выбираются эти параметры. Часто в качестве определяющей температуры принимают среднюю температуру пограничного слоя жидкости или газа

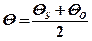(5.9)

Значения теплофизических параметров сред для различных температур приводятся в справочных таблицах (приложение2).

Безразмерные критерии в уравнении (5.4) характеризуют условия теплообмена. В частности, критерий Рейнольдса Rе характеризует скорость движения среды относительно твердого тела. Критерий Прандтля Pr характеризует способность теплоты распространяться в среде, критерий Грасгофа Gr учитывает влияние естественной конвекции внутри среды. Критерий Нуссельта служит для расчета коэффициента теплоотдачи α.

Анализ критериального уравнения (5.4) позволяет установить влияние различных факторов на величину коэффициента теплоотдачи. Коэффициент теплоотдачи α возрастает с увеличением теплопроводности среды, например, для воды при 20°С 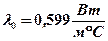, для масляных сред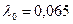 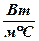, для воздуха .

Из этого следует, что теплоотдача в воду и водные растворы намного превышает ( ~ в10 раз) теплоотдачу в масляные среды и в 20 раз – в воздух. Коэффициент теплоотдачи α возрастает с увеличением скорости движения среды. Коэффициент теплоотдачи возрастает с увеличением перепада температур (Θ_S – Θ_O).