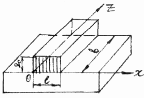
Инженерная методика расчета температур на контактных площадках тел

[1] с. 168 – 175.

Температуры на контактных площадках тел, возникающих под действием различных источников и стоков теплоты, могут быть расчитаны путем интегрирования соответствующих выражений. Однако, при сложных формах тел и законах распределения плотности тепловыделения эти расчеты весьма трудоемки, а в ряде случаев вообще невозможно выполнить интегрирование точными методами. Поэтому для практических целей с некоторой долей приближения можно использовать инженерную методику расчета температур.

Идея инженерной методики состоит в том, что формулы для расчета температур представляют в виде ряда сомножителей. Для удобства использования структура сомножителей соответствует структуре кода тепловых задач.

Код задач имеет вид 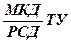, а формула для расчета температур

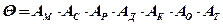(4.1)

Сомножители учитывают:

А_М – мерность источника;

А_С – скорость движения источника;

А_Р – закон распределения плотности тепловыделения источника или стока;

А_Д – длительность функционирования источника;

А_К – конфигурацию источника;

А_О – ограниченность источника;

А_Т – форму тела.

Значение каждого из сомножителей А зависит от значения символа в коде тепловой задачи.

В формулу не входит сомножитель А_У, учитывающий граничные условия на поверхностях тел. В технологических системах чаще всего встречаются два варианта граничных условий – ГУ2 и ГУ3. Формула (4.1) записана для граничных условий ГУ2, когда теплоотдачей с поверхностей, не занятых источниками и стоками теплоты, можно пренебречь. Условия ГУ3 (конвективный теплообмен) можно учесть соответствующими коэффициентами.

Формула (4.1) пригодна для расчета как средних Θ_ср так и наибольших Θ^max температур на контактной площадке. Поэтому каждый из сомножителей может иметь обозначение A^{с р} и A^max.

Инженерную методику расчета температур будем рассматривать при действии двумерных неподвижных и быстродвижущихся источников и стоков теплоты при граничных условиях второго рода (ГУ2), которые наиболее часто встречаются при тепловом анализе технологических систем.

Сомножитель А_м (мерность)

Для двумерных источников

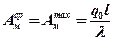, (4.2)

где q₀ – максимальная плотность тепловыделения, Вт/м² ;

λ – коэффициент теплопроводности, Вт/м°С;

l – характерный размер источника, м.

Характерный размер источника выбирается:

- для неподвижных источников – размер по оси х;

- для быстродвижущихся источников – размер по направлению движения;

- для круговых l = d, где d – диаметр пятна нагрева.

Сомножитель А_с (скорость).

Для неподвижных источников С = 0

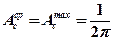; (4.3)

Для быстродвижущихся источников С = 2 зависит от числа Пекле

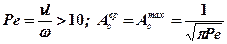; (4.4)

Сомножитель А_Р (закон распределения плотности тепловыделения) выбирается из таблицы 4.1.

Таблица 4.1 – Значения сомножителя А_Р

Закон распределения Р	С = О (неподвижный)	С = 2 (быстродвижущийся)
А	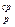А	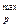А	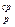А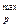
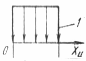
		3,06	3,31	0.67	1,0
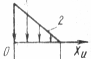
		1,53	1,76	0,40	0,47
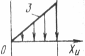
		1,53	1,76	0,27	0,67
		1,49	1,86	0,36	0,44
		1,49	1,86	0,20	0,54
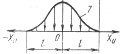
		2,7	3,0	0,29	0,49
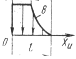
		–	–	0,51	0,71

 

 

Сомножитель А_Д (длительность)

При установившемся теплообмене (Д = 2)

 

 

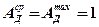
При неустановившемся теплообмене (Д = 1) зависит от величины критерия Фурье 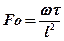и выбирается из таблицы 4.2.

 

Таблица 4.2 – Значения сомножителя А_Д

Fо	0,01	0,1	0,5
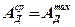
	0,107	0,315	0,534	0,653	0.857	0,942	0,968	1,0

 

Сомножитель А_К (конфигурация)

При К = 1, т.е. площадка, на которой действует источник, имеет вид бесконечной полосы или прямоугольника .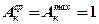

При К = 2 (круговой источник) и Д = 2 (установившийся теплообмен) выбираются из таблицы 4.3.

 

Таблица 4.3 – Значения сомножителя А_к

Закон распределения Р	С = 0 (неподвижный)	С = 2 (быстродвижущийся)
А	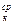А	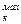А	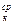А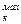
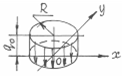
		0,43	0,47	0,68	0.85
		0,35	0,47	1,33	1,0

 

Сомножитель А_О (ограниченность)

Для неподвижных источников (С = 0):

– в виде неограниченной полосы (0 = 1) ;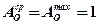

– для круговых (0 = 2) ;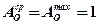

– для прямоугольных (0 = 2) зависит от параметра ,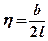

где b – ширина источника и выбирается из таблицы 4.4.

 

Таблица 4.4 – Значения сомножителя А_О

С = 0 (неподвижный)	η	0,5	1,0
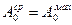
	0,52	0,75	0,85	0,90	0,95	0,96	0,97	0,99

 

Для быстродвижущихся источников (С = 2):

– в виде неограниченной полосы (0 = 1) ;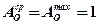

– для круговых (0 = 2)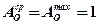

– для прямоугольных (0 = 2) зависит от параметра 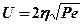и выбирается из таблицы 4.5.

 

Таблица 4.5 – Значения сомножителя А_О

C = 2 (быстодвижу- щийся)	U	0,5
А	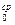0,45	0,50	0,72	0,81	0,85	0,87	0,89	0,9
А	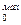0,39	0,60	0,80	0,95	1,0	1,0	1,0	1,0

 

Сомножитель А_Т (форма тела).

Для неограниченного пространства (Т = 0)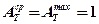

Для полупространства (Т = 1)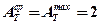

Для других тел зависит от параметра ,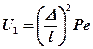

где Δ – толщина пластины или диаметр цилиндра;

l – характерный размер источника.

Для пластин (Т = 2), цилиндров (Т = 7)., клиньев (Т = 8) выбирается из таблицы 4.6.

 

Таблица 4.6 – Значения сомножителя А_T

С (скорость)	Т (форма тела)	Диапазон значений	А	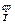А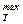
С=2 Быстро- движу-щийся	Т-2 пластина	0,1 ≤ u1 ≤ 1,6	2,14u	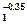2,36u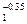
u1 > 1,6	2,0	2,0
Т=7 цилиндр	20 ≤ u1 ≤ 12·103	2,78u	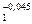3,06u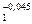
u1 > 12·103	2,0	2,0
С=0 Непод- вижный	Т=8 клин	45° ≤ β ≤ 120°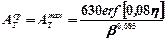

 

В последней формуле β – угол заострения клина, град., 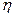= 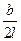. Величина интеграла вероятности erf[k] принимается по таблицам, либо может быть приближенно подсчитана по формуле

 

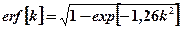(4.5)

 

Инженерная методика расчета температур на контактных площадках тел позволяет решать балансовые задачи. Эти задачи определяют плотность тепловых потоков теплообмена и законы распределения температур в местах соприкосновения тел технологической системы при граничных условиях четвертого рода (ГУ4).

Использование инженерной методики в решении балансовых задач покажем на примере.

 

Задача

 

Наружную поверхность заготовки из стали 20ХН3А упрочняют выглаживанием сферическим индентором из стали ШХ15 радиусом R=10мм (Рис. 4.1).

 

 

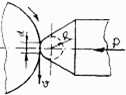
Рис. 4.1 – Процесс выглаживания поверхности индентором.

 

 

Скорость движения заготовки v = 1м/с; сила прижима индентора к заготовке Р = 1000Н. Коэффициент трения между заготовкой и индентором f = 0,12; диаметр пятна контакта d = 1мм. Необходимо рассчитать температуру на поверхности контакта между индентором и заготовкой.

Справочные данные: для стали 20ХН3А:

λ₁ = 33,5 Вт/м°С; ω = 0,066 10 ^{– 4} м²/с;

для стали ШХ15 – λ₂ = 33,4 Вт/м°С; ω = 0,065 10 ^{– 4}м²/с.

 

Решение:

 

1. Составляем структурную схему теплообмена.

Структурная схема представляет собой изображения схематизированных тел с относящимися к ним источниками и стоками теплоты, тела условно раздвинуты. (Рис. 4.2).

 

 

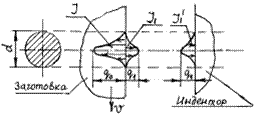
Рис. 4.2. Структурная схема теплообмена.

 

На схеме изображены:

I – источник тепловыделения,

I₁ – сток теплоты из заготовки в индентор,

I¹₁ – источник тепловыделения для индентора.

 

Для одного из двух тел, находящихся в контакте (заготовки), I₁ является стоком теплоты, Для другого тела (индентора) он является источником тепловыделения I¹₁, т.е.

I₁ = I¹₁.

 

Принимаем некоторые допущения и схематизируем задачу:

 

– из-за малых размеров пятна контакта по сравнению с размерами заготовки и индентором их можно представить как полупространства;

– на основе опытных данных источник тепловыделения I принимаем распределенным по нормальному круговому закону;

– сток теплоты I₁ также принимаем распределенным по тому же закону;

– будем считать процесс установившимся.

Рассчитываем наибольшую плотность тепловыделения источника I

 

W = Tv = Pfv = 1000 0,12 1 = 120 Вт,

 

где Т – сила трения на площадке контакта.

 

2. Для кругового источника с нормальным законом распределения плотности тепловыделения (формула2.10)

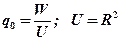, где R – радиус пятна нагрева; ;

 

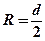тогда 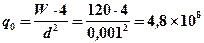Вт/м².

 

3. Рассчитываем критерий Пекле для источника I и стока I₁ (на заготовке они движущиеся)

 

 

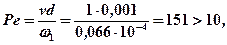
т.е. источник быстродвижущийся.

4. Составляем коды тепловых задач

 

– для заготовки: источник I: М = 2; К = 2; О = 2; Р = 707; С = 2; Д = 2; Т = 1; У = 2;

сток теплоты I₁: М = 2; К = 2; О = 2; Р = 707; С = 2; Д = 2; Т = 1;У = 2

 

+ .

 

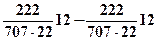Знак + указывает, что это источник теплоты.

Знак – указывает, что это сток теплоты.

 

– для индентора: источник I¹₁ неподвижный М = 2; К = 2; О = 2;

Р = 707; С = 0; Д = 2; Т = 1; У = 2

 

+ .

 

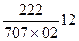5. Рассчитываем среднюю и максимальную температуру на контактной площадке заготовки:

 

итоговая плотность теплового потока на заготовке

q = q₀ – q₁ = 4,8·10⁸ – q₁

 

Используем инженерную методику расчета. Определяем сомножители

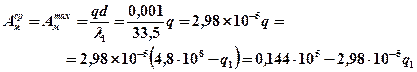
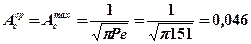(источник быстродвижущийся)

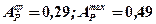( по таблице 4.1).

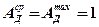(установившийся теплообмен).

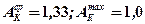(по таблице 4.3)

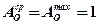(источник круговой)

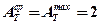(полупространство).

Подставляя сомножители, имеем :

 

 

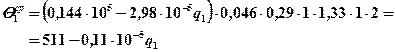
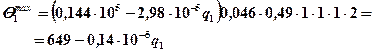
6. Аналогично рассчитываем среднюю и максимальную температуру на контактной площадке индентора

 

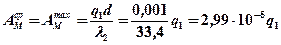
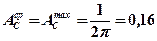(источник неподвижный)

;

;

;

;

.

 

;

.

 

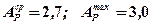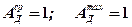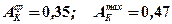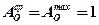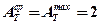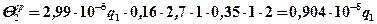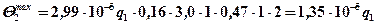7. Решаем балансовую задачу.

 

В первом варианте принимаем условие равенства средних температур на контактной площадке, т. е.

;

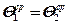Тогда ,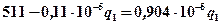

Откуда

 

 

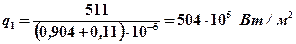
Средние температуры

На заготовке

 

 

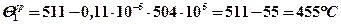
На инденторе ,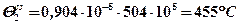

что подтверждает принятое допущение.

Во втором варианте принимаем условие равенства максимальных температур в некоторых точках контактной площадки, т. е.

 

.

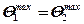Аналогично получаем

 

 

;

 

 

.

 

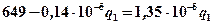
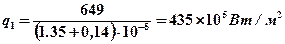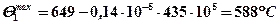
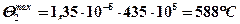Естественно, что максимальные температуры получились большими, чем средние. Следует отметить, что изложенная методика расчета позволяет рассчитать избыточные температуры, превышающие температуру окружающей среды. Для определения температуры в обычном понимании необходимо к расчетным данным прибавлять температуру окружающей среды.

 

Вопросы для самопроверки

 

1. Каковы особенности структурной схемы теплообмена в системе тел? Что дает применение структурных схем?

2. Изложите основные принципы инженерной методики расчета температур на контактных поверхностях тел.

 

 

Задачи

 

1.   Рис. 4.3 – Схема полосового источника

Составить код задачи и рассчитать среднюю и максимальную температуры контактной площадки при действии неподвижного источника теплоты с равномерным распределением плотности тепловыделения на поверхности стержня прямоугольного сечения.   Материал стержня – сталь 45 с теплофизическими свойствами: λ = 40,2 Вт/м°С, ω = 0,08·10–4 м2/с. Размеры источника b = 5 мм, l = 2 мм, мощность источника W = 150 Вт. При решении принять источник как полосовой, ограниченный вдоль одной оси, стержень как полупространство. Теплообмен считать установившимся при ГУ2.

 

2. 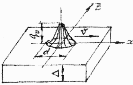Рис. 4.4 – Схема кругового источника

Составить код задачи и рассчитать среднюю и максимальную температуры контактной площадки при действии движущегося кругового источника теплоты с нормальным симметричным распределением плотности тепловыделения на поверхности пластины. Материал пластины – твердый сплав ВК8 с теплофизическими свойствами: λ= 54,4 Вт/м°С, ω = 0,246·10–4 м2/с. Диаметр источника d = 8 мм, скорость движения v = 0,1 м/с, мощность W = 1,5 кВт. Толщина пластины Δ = 4 мм. Теплообмен считать установившимся при ГУ2.

3. 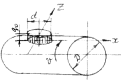Рис. 4.5 – Схема кругового источника

Составить код задачи и рассчитать среднюю и максимальную температуры контактной площадки при действии движущегося кругового источника теплоты с равномерным распределением плотности тепловыделения на поверхности цилиндра. Материал цилиндра – сталь 12Х18Н9Т с теплофизическим и свойствами. λ= 22,6 Вт/м°С, ω = 0,05·10 –4 м2 /с. Диаметр источника d = 3 мм, мощность W = 80 Вт, скорость движения v = 0,05 м/с. Диаметр цилиндра D = 150 мм. Теплообмен считать установившимся при ГУ2.

 

4. 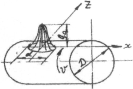Рис. 4.6 – Схема кругового источника

Составить код задачи и рассчитать. среднюю и максимальную температуры контактной площадки при действии движущегося кругового источника теплоты с нормальным симметричным распределением плотности тепловыделения на поверхности цилиндра. Материал цилиндра – жаропрочный сплав ВТ4 с теплофизическими свойствами: λ= 12,9 Вт/м°С. ω = 0,043·10 –4м2/с, Диаметр источника d = 4 мм, скорость движения v = 0,05 м/с, мощность W = 200 Вт. Диаметр цилиндра D = 40 мм Теплообмен считать установившимся при ГУ2.

 

5. 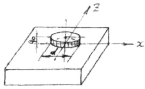Рис. 4.7 – Схема кругового источника

Составить код задачи и рассчитать среднюю и максимальную температуры контактной площадки при действии неподвижного кругового источника теплоты с равномерным распределением плотности тепловыделения на поверхности стержня прямоугольного сечения. Материал стержня – сталь ЗОХГС с теплофизическими свойствами: λ= 36 Вт/м°С, ω = 0,07 10–4 м2/c. Диаметр источника d = 5 мм, мощность W = 90 Вт. Принять стержень как полупространство Теплообмен считать установившимся при ГУ2.

 

<10111213141516>

---

Дата добавления: 2020-06-09; просмотров: 432;

---