Основное уравнение турбомашин Эйлера
Воспользуемся теорией об изменении момента количества движения и сформулируем ее для потока жидкости в рабочем колесе межлопаточных каналов.
Изменение момента количества движения потока времени где 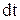 относительно оси вращения рабочего колеса равно импульсу момента всех внешних сил, действующих на поток, относительно той же оси, т.е. импульсу крутящего момента на валу насоса.
относительно оси вращения рабочего колеса равно импульсу момента всех внешних сил, действующих на поток, относительно той же оси, т.е. импульсу крутящего момента на валу насоса.
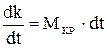
Пусть жидкость массой m движется с абсолютной скоростью С, тогда количество движения этой массы составит вектор 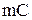 , направление которого совпадает с направлением вектора скорости С.
, направление которого совпадает с направлением вектора скорости С.
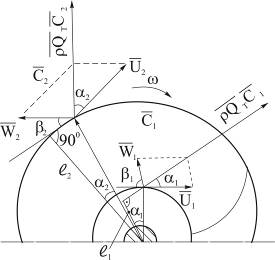
Рисунок 3.12
Момент количества движения массы относительно оси вращения рабочего колеса, как это показано на рисунке 3.12, составит:
на входе в лопастное колесо
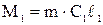 ,
,
на выходе из колеса
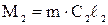
где m - масса жидкости, вошедшая в межлопаточные каналы и вышедшая из них за время dt, которую можно выразить через объемный расход 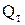 и плотность
и плотность 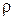 :
:
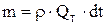 ,
,
где 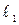 и
и 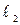 - плечи, представляющие собой перпендикуляры, опущенные из центра вращения колеса на направление вектора абсолютной скорости.
- плечи, представляющие собой перпендикуляры, опущенные из центра вращения колеса на направление вектора абсолютной скорости.
Плечи 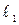 и
и 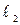 можно заменить соответственно через радиусы входа и выхода жидкости из рабочего колеса:
можно заменить соответственно через радиусы входа и выхода жидкости из рабочего колеса:
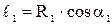 ,
, 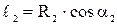
Изменение момента количество движения равно:
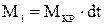
Подставляя значения M1 и M2, получим:
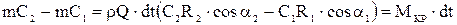
Итак, левая часть исходного уравнения равна:
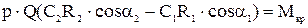
Правая часть исходного уравнения представляет собой момент внешних сил, действующих на поток относительно оси вращения рабочего колеса, т.е. крутящий момент на валу насоса.
Момент 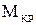 умножим на угловую скорость вращения колеса
умножим на угловую скорость вращения колеса 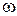 - это составит мощность на валу насоса, т.е. потребляемую мощность:
- это составит мощность на валу насоса, т.е. потребляемую мощность:
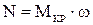
Приращение энергии потока жидкости в рабочем колесе, т.е. полезная мощность насоса:
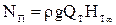
где 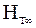 - теоретический напор при бесконечном числе лопаток.
- теоретический напор при бесконечном числе лопаток.
В данном случае 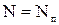 ,т.к. жидкость идеальная и вся потребляемая мощность переходит в полезную.
,т.к. жидкость идеальная и вся потребляемая мощность переходит в полезную.
Из условия 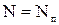
вытекает:
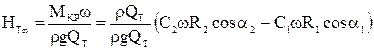 , т.к.
, т.к. 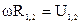 , то
, то
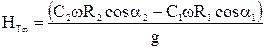 .
.
Полученное уравнение называют уравнением Эйлера для турбомашин.
Если вход жидкости в рабочее колесо насоса радиальный ( 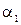 =90°), как это имеет место у большинства центробежных насосов (закрутка потока отсутствует), т.е.
=90°), как это имеет место у большинства центробежных насосов (закрутка потока отсутствует), т.е. 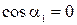 , то уравнение Эйлера записывается в следующем виде:
, то уравнение Эйлера записывается в следующем виде:
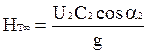
Дата добавления: 2016-06-29; просмотров: 2720;











