Преобразование энергии в турбинной ступени

Преобразование энергии в турбинной ступени, а также энергетические характеристики других элементов проточной части турбины описываются в общем случае на основе законов течения сжимаемой жидкости, которые изучаются в курсе гидрогазодинамики. В основном используются законы одномерного движения, под которым понимают такое движение жидкости, когда во всех точках поперечного сечения канала параметры жидкости (скорость, давление, удельный объем и др.) можно считать постоянным, а изменение параметров происходит вдоль канала. В реальных потоках рабочего тела в паровых турбинах параметры в поперечном сечении канала не сохраняются постоянными. Например, скорость потока вблизи стенок вследствие трения всегда ниже, чем в ядре потока.

Вторым существенным допущением при расчете потоков в проточной части турбины является предположение о неизменности параметров потока во времени, т.е. поток рассматривается установившимся.

Кроме этого делаются и другие допущения – например, об отсутствии теплообмена между потоком и стенками каналов и др.

Основными уравнениями одномерного движения сжимаемой жидкости являются:

1) уравнение состояния: 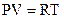(примером можно назвать h,s–диаграмму);

2) уравнение неразрывности, расхода, сплошности: 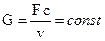- для любого поперечного сечения одномерного установившегося потока расход массы есть величина const для данного потока,

где F – площадь поперечного сечения; c – скорость; v – удельный объем.

3) уравнение количества движения: ;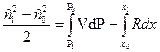

4) уравнение сохранения энергии: 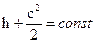- для 1 кг массы рабочего тела любого поперечного сечения одномерного потока сумма энтальпии и кинетической энергии есть величина постоянная для данного потока.

Одномерные течения в каналах разделяются на конфузорные и диффузорные.

Конфузорными называются такие течения в каналах, когда скорость рабочего тела на выходе становится больше, чем скорость на входе.

Диффузорными называются течения, в которых скорость рабочего тела уменьшается в направлении потока.

Основные уравнения одномерных потоков позволяют рассчитывать течения в каналах турбомашин. Из уравнения сохранения энергии следует, что при конфузорном течении, например, в соплах турбины, вдоль потока вместе с увеличением скорости рабочего тела уменьшается его энтальпия; в диффузорных потоках, наоборот, энтальпия растет, т.к. скорость падает.

Для расчетов одномерных потоков в каналах вводят параметры полного торможения потока в данном его сечении. Под ними в каком либо сечении понимают фиктивные параметры, которые достигаются при полном изоэнтропном торможении потока от состояния в этом сечении до нулевой скорости.

Параметры полного торможения могут быть подсчитаны с помощью h,s-диаграммы. Изобразим процесс течения рабочего тела в сопловом канале в h,s-диаграмме (рис.21).

Параметры во входном сечении сопла обозначены с индексом О, а в сечении на выходе из сопла с индексом 1, если течение реальное с потерями энергии, и с индексом 1t, если течение предполагается изоэнтропным (без потерь энергии).

Для определения скорости на выходе из соплового канала при изоэнтропном течении используем уравнение энергии, записанное для входного и выходного сечений сопла: ,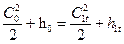

откуда теоретическая скорость на выходе из сопла ,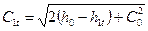

где 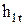находится по давлению 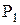в выходном сечении сопла (например, из h,s-диаграммы).

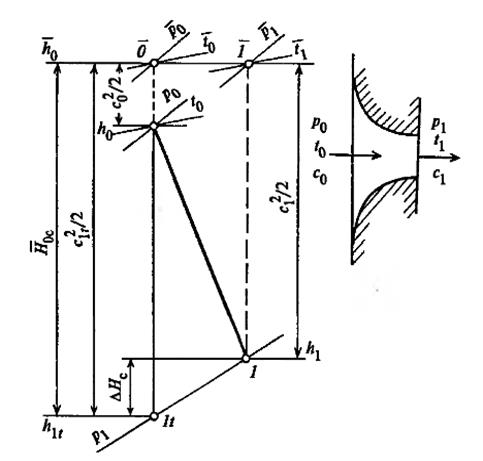
Рисунок 21 – Процесс изменения состояния в h,s–диаграмме при

истечении пара или газа через сопло

Действительная скорость потока (с потерями энергии) на выходе из сопла определяется по аналогичной формуле, полученной из уравнения энергии, записанного для входного и выходного сечений сопла по действительным параметрам потока за соплом ; .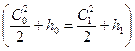

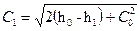Разность энтальпий 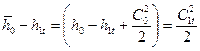называют располагаемым теплоперепадом сопл и обозначают .

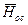Для определения параметров полного торможения во входном сечении сопла следует на h,s-диаграмме от точки О вверх по изоэнтропе отложить отрезок 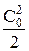, соответствующий кинетической энергии скорости потока на входе в сопло.

Через точку 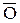в конце этого отрезка проходят изобара 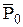, изотерма 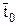, линия энтальпии полного торможения 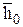и другие линии параметров полного торможения.

Аналогично для определения параметров полного торможения в выходном сечении сопла следует отложить в h,s-диаграмме от точки 1 вверх по изоэнтропе отрезок 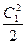, соответствующий кинетической энергии потока на выходе из сопла. Через точку 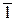в конце этого отрезка проходят изобара давления полного торможения 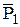и изотерма температуры полного торможения .

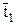Таким образом, в потоках с потерями кинетической энергии давление полного торможения уменьшается вдоль потока.

В отличие от параметров полного торможения 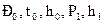называют статическими давлением, температурой, энтальпией в соответствующих сечениях.

Разность энтальпий 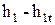эквивалентна работе, совершенной газом против сил трения при реальном течении, которая превращается в теплоту и передается потоку при низком давлении. Другими словами, 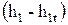представляет собой потери кинетической энергии потока вследствие трения и других необратимых процессов в потоке. Для сопл эта величина потерь энергии 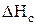вычисляется из уравнений сохранения энергии для теоретического и реального потоков

.

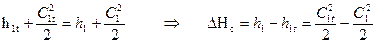Каналы, в которых происходит плавное преобразование энтальпии в кинетическую энергию, т.е. в которых происходит ускорение потока, называется сопловыми или просто соплами.

Для характеристики потоков важными являются понятия скорости звука и критической скорости потока: .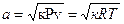

Критической скоростью потока 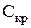называется скорость газа в том сечении, где она равна местной скорости звука 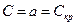. Сечение, где скорость потока достигает критической скорости, называется критическим. Параметры потока этого сечения называются также критическими ( ).

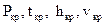Как следует из 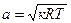, местная скорость звука зависит только от статической температуры в том сечении потока, в котором вычисляется скорость звука. Следовательно, критическая скорость потока определяется по критической температуре потока .

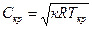Для расчетов потока важными являются безразмерные параметры потока. К ним относятся: относительное давление 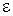, равное отношению статического давления к давлению полного торможения в данном сечении, относительная температура и т.п. К безразмерным параметрам потоков относятся также безразмерные величины М и .

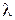М=С/а - отношение скорости потока к скорости звука в данном сечении называется числом Маха.

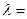С/С_кр- безмерная скорость, определяется как отношение скорости потока в данном сечении к критической скорости потока.

Между любыми двумя безмерными параметрами легко устанавливаются функциональные зависимости, которые носят название газодинамических функций, приведенных в справочной литературе и известных из курса гидрогазодинамики.

Поскольку в состав турбинной ступени входят турбинная решетка, то вкратце остановимся на ее рассмотрении.

В паровых турбинах широко используется кольцевые турбинные решетки (рис.22), представляющие собой систему каналов, образованную установленными по кольцу одинаковыми профилями специальной формы. Все профили в решетке одинаковы, их устанавливают на равном расстоянии друг от друга и одинаковым образом. В результате между профилями образуются каналы, через которые вытекает пар.

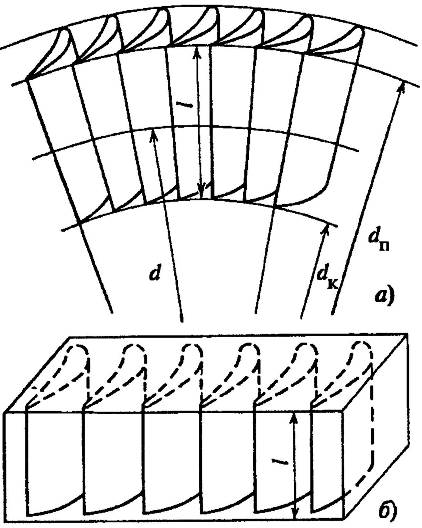
Рисунок 22 - Модели турбинных решеток: а – кольцевой; б – прямой (плоской)

Путем изменения формы профилей и расположения их в решетке можно получать необходимую форму каналов (рис.23).

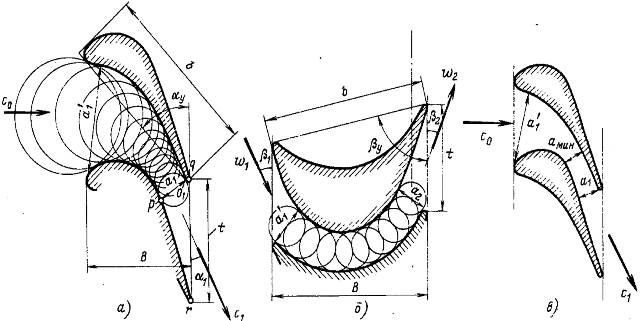
Рисунок 23 - Развертки профилей турбинных решеток: а, б - с каналами сильно и слабо уменьшающегося сечения; в - с каналами типа сопла Лаваля

Входная часть профиля называется входной кромкой, выходная – выходной кромкой, выпуклая часть – спинкой или стороной разрежения, вогнутая - стороной давления. Выходная часть канала называется косым срезом.

Течение пара в турбинных решетках подчиняется общим закономерностям, рассмотренным ранее.

Потери энергии, возникающие при течении пара через турбинную решетку, условно можно разделить на несколько составляющих. Значительную долю потерь составляют профильные, которые возникают при обтекании потоком профилей за счет появления сил трения. Имеют место также концевые потери, возникающие в концевых областях лопаток и вызывающие появление вихрей. За счет улучшения профиля лопаток, их лучшего обтекания потоком, понижаются потери.

Под турбинной ступенью, как отмечалось ранее, понимается совокупность неподвижного ряда сопловых лопаток, в каналах которых ускоряется поток пара или газа, и подвижного ряда рабочих лопаток, в которых энергия движущегося пара или газа преобразуется в механическую работу на вращающемся роторе по преодолению сил сопротивления приводимой машины. На рис.24 приведено схематическое изображение турбинной ступени.

Турбинная ступень характеризуется средним диаметром ступени d и высотами сопловых l₁ и рабочих l₂ лопаток.

Сопловые лопатки со строго одинаковым шагом установлены в диафрагме, представляющей собой плоское, разрезанное по горизонтальному диаметру, кольцо. Сопловые лопатки образуют кольцевую решетку.

Рабочие лопатки с помощью хвостовиков набираются на диске, откованном заодно с валом или посаженном на него с натягом. Подобно сопловым лопаткам, рабочие лопатки образуют кольцевую решетку. Соседние лопатки решетки образуют рабочие каналы, через которые проходят струи пара, выходящие из сопловой решетки.

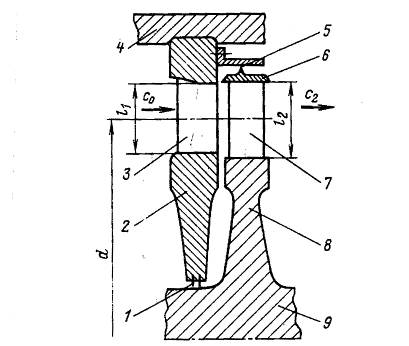
Рисунок 24 - Схематическое изображение турбинной ступени:

1 – диафрагменное уплотнение; 2 – диафрагма; 3 – сопловая решетка; 4 – корпус турбины; 5 – надбандажное уплотнение; 6 – ленточный бандаж; 7 – рабочая решетка; 8 – диск; 9 – вал

Рабочие лопатки, набранные на диске, обычно связаны по вершинам с помощью ленточного бандажа в пакеты по 2-14 шт. для увеличения надежности и экономичности ступени. Поверх бандажа часто устанавливают уплотнения для уменьшения утечки пара над бандажом. Аналогичное уплотнение устанавливают между диафрагмой и валом.

При истечении пара из сопла в среду с пониженным давлением его потенциальная энергия переходит в кинетическую. Именно такой процесс происходит в сопловых каналах турбинной установки. За счет понижения давления от значения 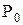перед сопловой решеткой до давления 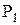за ней скорость пара за сопловой решеткой 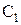будет больше скорости 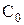на входе в решетку. Таким образом, на выходе из сопловой решетки образуется кольцевая струя пара, скорость которой достигает нескольких сотен м/с. Эта струя пара под малым углом к плоскости диска входит в каналы рабочей решетки и, поворачиваясь, выходит из них.

На выходе из сопловых лопаток рабочее тело (пар или газ) приобретает в процессе расширения скорость 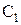, направленную под углом 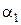к вектору окружной скорости рабочих лопаток U. Направление потока под углом задается соответствующей формой и установкой сопловых лопаток (рис.25). Рабочие лопатки перемешаются перед соплами с окружной скоростью U.

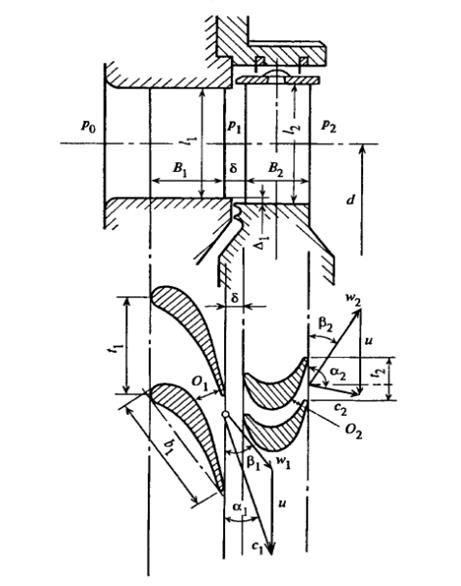
Рисунок 25 - Проточная часть осевой ступени и развертка цилиндрического сечения по среднему диаметру ступени : 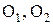- размеры горла сопловых и рабочих решеток

Значение этой скорости зависит от диаметра d, на котором расположены рабочие лопатки, и от частоты вращения ротора n: .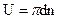

На входе в рабочие лопатки рабочее тело в относительном движении перемещается с относительной скоростью 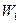. Вектор относительной скорости, как известно, определяется геометрическим вычитанием абсолютной и окружной скоростей. Векторы абсолютной, окружной и относительной скоростей образуют треугольник скоростей на входе в рабочие лопатки. Угол между векторами относительной и окружной (переносной) скоростей обозначают 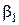. Направление входных кромок рабочих лопаток при изготовлении определяется направлением относительной скорости, т.е. углом 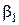. При течении в каналах рабочих лопаток происходит дальнейшее расширение рабочего тела от давления 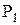до давления 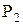за рабочими лопатками, а также поворот потока. За счет поворота потока и расширения рабочего тела на рабочих лопатках создается крутящий момент на роторе, который и производит работу по преодолению сил сопротивления приводимой машины. За счет поворота потока в каналах рабочих лопаток создается активная часть усилия, а за счет ускорения потока в каналах рабочих лопаток - реактивная часть усилия, действующего на рабочие лопатки.

На выходе из каналов рабочих лопаток относительная скорость рабочего тела обозначается 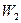и определяется кинетической энергией в относительном движении на входе в каналы рабочей решетки и энергией при расширении рабочего тела от давления 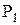до давления 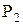. Сложив векторы относительной и окружной (переносной) скоростей, получим вектор абсолютной скорости 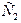. Угол вектора скорости 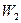с направлением, обратным 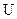, обозначают 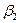, а его значение определяется формой профиля рабочей лопатки и ее установкой на роторе; при этом направлением выходной кромки рабочей лопатки определяется направление относительной скорости потока на выходе из рабочих лопаток. Угол вектора скорости 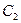с направлением, обратным 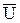, обозначают 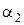. 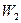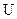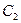Треугольник скоростей, образованный векторами , и , называют выходным.

Рассмотрим процесс течения рабочего тела в турбинной ступени в h,s-диаграмме (рис.26).

Расширение рабочего тела в сопловых каналах ступени от состояния перед ступенью, определяемое точкой О, до точки 1t соответствует теоретическому (изоэнтропному) процессу течения в соплах. Реальный процесс в соплах сопровождается потерями энергии 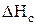, которые в виде теплоты вновь возвращаются в поток и повышают энтальпию за соплами. Действительное состояние рабочего тела за соплами изображается точной 1. Разность энтальпий ( 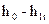) в сумме с кинетической энергией на входе в сопла 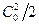составляет располагаемую энергию в соплах 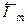, равную кинетической энергии потока на выходе из сопл 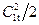при истечении без потерь энергии.

В соответствии с уравнением энергии теоретическая скорость потока на выходе из сопл определяется по формуле: .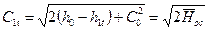

Действительная скорость истечения из сопл из-за потерь энергии в соплах меньше теоретической : ,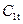

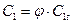где 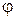- коэффициент скорости сопл.

Теоретический процесс расширения рабочего тела в рабочих лопатках изображается линией от точки 1 до точки 2t; разность ( 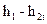) обозначается 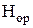и называется располагаемым теплоперепадом рабочих лопаток, и представляет собой потери энергии в рабочих лопатках .

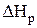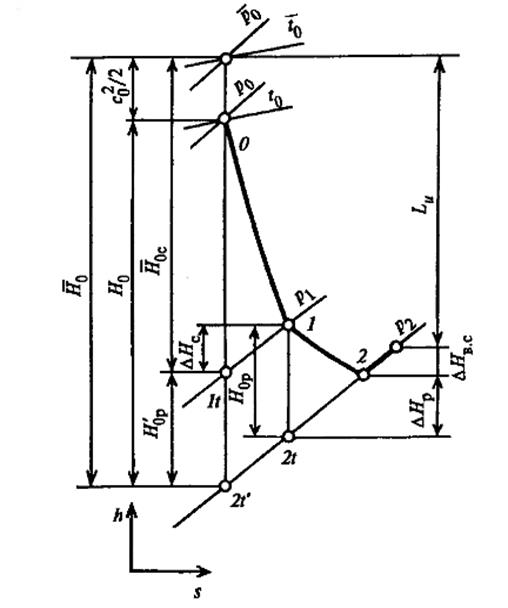
Рисунок 26 – Процесс течения пара (газа) в турбинной ступени в h,s–диаграмме

Для потока в относительном движении в каналах рабочих лопаток уравнение сохранения энергии для сечений на входе и выходе из каналов рабочих лопаток запишется в следующем виде: .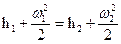

В правой части этого уравнения отсутствует член, характеризующий отводимую от рабочих лопаток к ротору турбины механическую работу, т.к. механическая работа силы взаимодействия между лопаткой и потоком в координатах движущейся лопатки равна нулю. Действительно, точка приложения этой силы не перемещается по отношению к наблюдателю, вращающемуся вместе с рабочими лопатками (условно). Перемещение точки приложения силы входит сомножителем в выражение механической работы.

По аналогии с предыдущими формулами получим выражение для определения теоретической скорости потока в относительном движении на выходе из рабочих лопаток: .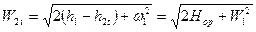

Действительная скорость на выходе из рабочих лопаток будет меньше теоретической : ,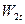

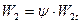где 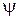- коэффициент скорости рабочих лопаток.

Потери энергии 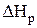находятся по формуле: .

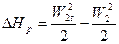Отрезок 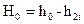изображает располагаемый теплоперепад ступени по статическим параметрам, а отрезок 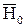, включающий кинетическую энергию скорости на входе в сопла 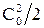, изображает располагаемый теплоперепад ступени по параметрам полного торможения перед ступенью и статическому давлению за ступенью. Если на выходе из рабочих лопаток поток, обладающий кинетической энергией 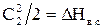, попадает в емкую камеру, то эта энергия расходуется на повышение температуры рабочего тела вследствие изобарического торможения в этой камере. Величина 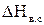называется потерей энергии с выходной скоростью ступени и изображается в h,s-диаграмме как показано на рис.26.

Треугольники скоростей на входе и выходе из рабочих лопаток при расчете турбинной ступени обычно совмещают вершинами в одну точку.

Для построения треугольников скоростей (рис.27) угол 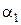вектора скорости 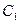выбирают в интервале от 11 до 20-25⁰. Значение 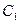определяют по формуле: .

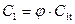Окружную скорость по формуле:

,

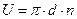где d – средний диаметр ротора, м;

n- частота вращения ротора, 1/с.

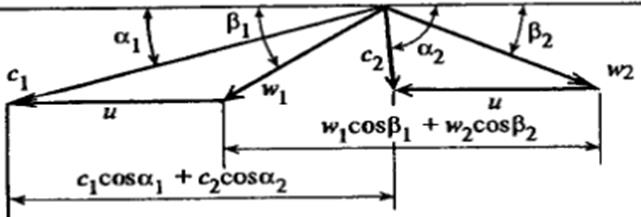
Рисунок 27 - Треугольники скоростей для потока пара (газа) в одновенечной турбинной ступени

Из геометрии входного треугольника скоростей определяют относительную скорость 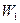и угол 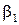. Для построения выходного треугольника скоростей по формуле: 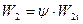определяют относительную скорость 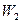. Угол 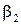вектора скорости 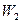обычно вычисляют по уравнению неразрывности, составленному для выходного сечения рабочих лопаток. Значения абсолютной скорости 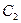и угла 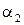определяют из геометрии выходного треугольника.

Соотношения между скоростями и углами потока в турбинной ступени в большой степени зависят от степени реактивности ступени 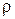. Под степенью реактивности ступени понимается отношение располагаемого теплоперепада рабочих лопаток к сумме располагаемых теплоперепадов сопловых и рабочих лопаток, которая приближенно равна располагаемому теплоперепаду ступени от параметров торможения:

.

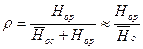Чем выше степень реактивности 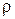, тем больше ускоряется поток в рабочих лопатках и, следовательно, относительная скорость на выходе 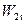увеличивается по сравнению со скоростью 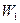. Ступень со степенью реактивности, равной нулю, называется активной. В активной ступени в рабочих лопатках не происходит расширения рабочего тела, давление перед рабочими лопатками равно давлению за ними 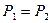. Турбинные ступени с 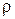=0,2-0,25 относят также к активному типу. Турбинные ступени с 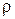=0,4-0,6 и более называют реактивными. В многоступенчатых реактивных турбинах обычно применяют реактивные ступени со степенью реактивности 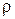=0,5.

Как правило, чисто активные ступени ( 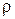=0) не используют на практике. Реальные активные ступени всегда имеют некоторую положительную реактивность для обеспечения конфузорности течения в каналах рабочих лопаток. Как известно из гидрогазодинамики, при конфузорности течения снижаются потери энергии в потоке.

В специальных случаях применяются ступени с отрицательной степенью реактивности. В рабочих лопатках ступени с 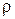<0 возникает диффузное течение, т.е. в каналах рабочих лопаток давление увеличивается к выходу 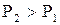. При этом диффузорное течение сопровождается повышенными потерями энергии в каналах рабочих лопаток.