Относительный лопаточный КПД ступени

Совершенство турбинной ступени характеризуется коэффициентом полезного действия. Относительным лопаточным КПД турбинной ступени называется отношение мощности, развиваемой на рабочих лопатках, к располагаемой мощности ступени: .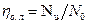

Если записать мощности, входящие в это уравнение, как произведения расхода рабочего тела через ступень на соответствующую удельную энергию: 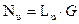и ,

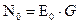то выражение для относительного лопаточного КПД будет иметь вид: .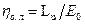

В этой формуле значение 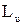может быть определено по уравнению количества движения или из баланса потерь энергии в ступени.

Располагаемая энергия ступени 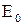определяется в зависимости от места расположения ступени в проточной части многоступенчатой турбины. Если за ступенью находится емкая камера, где поток, выходящий из ступени, тормозится и энергия выходной скорости в связи с этим не используется в последующих ступенях, .

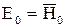Для промежуточной ступени, энергия выходной скорости которой используется в последующей ступени, в располагаемую энергию данной ступени эту энергию не включают, т.е. .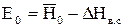

В общем случае располагаемую энергию ступени записывают: 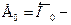ℋ_в.с ,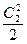

где 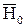- располагаемый теплоперепад ступени по параметрам торможения перед ступенью; ℋ_в.с 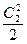– часть кинетической энергии выходной скорости данной ступени, используемая в последующей ступени, причем коэффициент выходной скорости ℋ_в.с может изменяться от нуля до единицы.

В частности, для ступени, за которой следует емкая камера, ℋ_в.с=0. Для большей части промежуточных ступеней энергия выходной скорости может быть полностью использована в последующей ступени, в этом случае ℋ_в.с =1.

Рассмотрим детальное изображение процесса в h,s-диаграмме для случая, когда значение коэффициента ℋ_в.с меньше единицы (рис.29).

При этом часть кинетической энергии выходной скорости (1- ℋ_в.с) 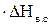теряется полностью; за ступенью эта энергия расходуется на повышение температуры рабочего тела при постоянном давлении (на изобарическое торможение). Другая часть кинетической энергии, равная ℋ_в.с 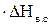, используется в последующей ступени для совершения механической работы. Для последующей ступени эта часть энергии будет составлять энергию входной скорости .

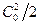Подставив в формулу 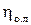выражение 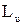, получим выражение для относительного лопаточного КПД ступени через проекции абсолютных и относительных скоростей:

.

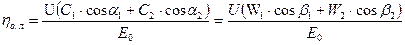Из этой формулы следует, что относительный лопаточный КПД ступени зависит от значений и направлений скоростей. Рассмотрим, от каких факторов зависит относительный лопаточный КПД ступени, т.е. попытается выяснить основные безразмерные параметры, определяющие 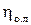. Для этого введем понятие фиктивной скорости 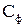определяемой из соотношения: 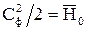. Преобразуем вначале формулу 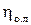для простейшего случая одиночной чисто активной ступени 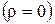. При этом используем следующие очевидные соотношения для этой ступени: 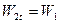; 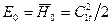, т.к. 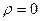и ℋ_в.с=0; 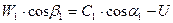(из треугольников скоростей для любой ступени).

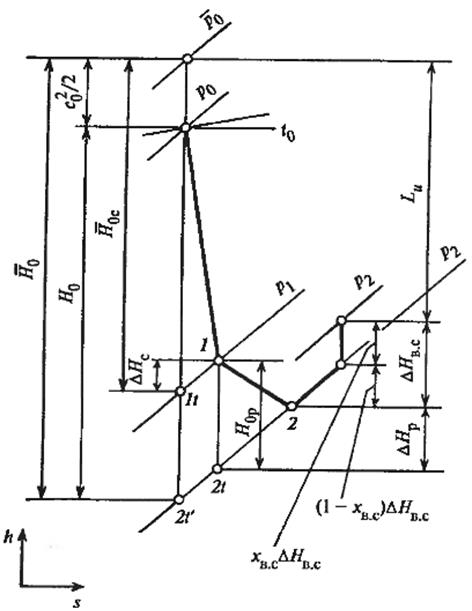
Рисунок 29 – Процесс течения в h,s–диаграмме для турбинной ступени

с частичным использованием энергии выходной скорости в последующей ступени

Для случая активной ступени , .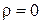

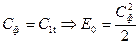Подставив перечисленные соотношения, можно выражение для 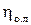преобразовать следующим образом:

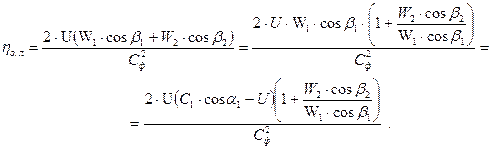
Т.к. для чисто активной ступен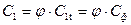и и 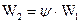, окончательно получаем: .

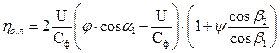Таким образом, 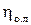чисто активной ступени зависит от соотношения скоростей U/C_ф, коэффициентов скоросте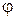й и 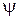, углов выхода из сопловых и рабочих лопаток 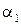и 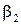. Угол 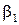есть функция 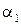, U/C_ф, 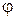и поэтому не является независимым параметром. Их перечисленных параметров на значение 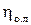в наибольшей степени оказывает влияние отношение скоростей U/C_ф, которое может изменяться в зависимости от окружной скорости при переменной частоте вращения ротора турбины или от скорости 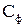при изменении располагаемого теплоперепада ступени 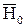, поэтому U/C_ф является важным параметром, определяющим КПД ступени. При фиксированных значениях 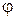, , 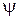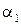и 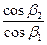зависимость 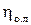от U/C_ф является квадратичной параболой.

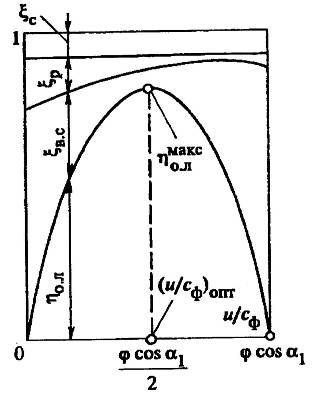
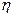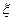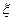Рисунок 30 - Зависимость _ол и потерь энергии _{с, р} и 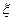_в.с от отношения скоростей U/C_ф для ступени со степенью реактивности 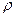=0

Парабола пересекает ось абсцисс при значениях 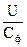=0 и 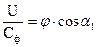, т.к. в этих точках 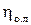=0. Максимальное значение КПД достигается при оптимальном отношении скоростей 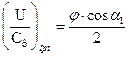. В этом случае для чисто активной ступени: 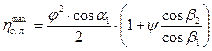. Отсюда следует, что максимум КПД для чисто активной ступени в большей степени зависит от коэффициента скорости сопловых лопаток 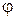и в меньшей степени от коэффициента скорости рабочих лопаток 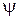. Так увеличение 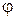на 0,01 приводит к увеличению 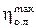на 0,017, а такое же приращение 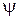вызывает прирост КПД всего лишь на 0,04. Таким образом, для активных ступеней наиболее важным является аэродинамическое совершенство сопловых лопаток, но при этом важным является и совершенство рабочих лопаток.

Параболическая зависимость КПД от U/C_ф отражает баланс энергии в чисто активной ступени. Из него можно получить зависимость, справедливую для ступени с любой степенью реактивности:

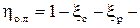(1- ℋ_в.с) ,

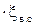где 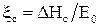, , 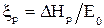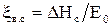- относительные потери энергии в соплах, рабочих лопатках и с выходной скоростью ступени. Величины потерь представлены на рис.30 и зависят от U/C_ф 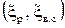или нет .

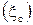Зависимость 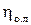для ступеней со степенью реактивности, отличной от нуля, имеет следующий вид:

.

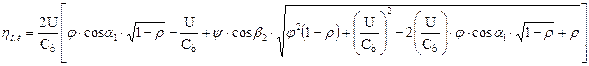Видно, что относительный лопаточный КПД ступени с любой степенью реактивности зависит от U/C_ф, 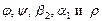и достигает максимума при некотором значении (U/C_ф)_opt, зависящего от 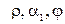и определяется минимальным значением потерь энергии с выходной скоростью, т.е. 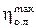соответствует режиму работы ступени, при котором угол 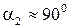. Используя это условие, можно прийти к виду: .

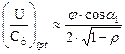На рис.31 представлена зависимость 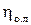и потерь энергии в ступени с 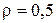от отношения скоростей U/C_ф.

Сравнивая ступени с 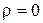и 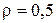, замечаем, что (U/C_ф)_opt для второй ступени в 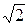раз больше, чем для первой. Следовательно, при одинаковых окружных скоростях и оптимальных U/C_ф располагаемый теплоперепад ступени с 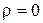в два раза больше теплоперепада ступени с 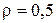. Соответственно число ступеней в реактивной турбине существенно больше, чем в активной и .

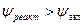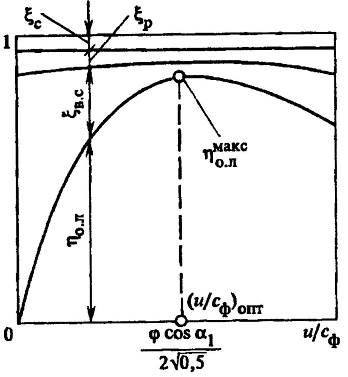
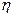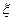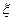Рисунок 31 – Зависимость КПД _ол и потерь энергии _{с, р} и 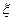_в.с от отношения скоростей U/C_ф для ступени со степенью реактивности 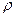=0,5