Классификация методов расчетов надежности

Главным назначением расчетов надежности следует считать:

- сравнительный анализ различных конструктивных (схемных) вариантов изделия на стадии его проектирования для обоснованного выбора комплектующих элементов, общей структурной схемы, способов резервирования, методов контроля и обслуживания;

- ориентировочная, прогнозируемая оценка надежности изделия на этапе утверждения технического проекта для обоснования вывода о том, что проектируемое изделие может быть изготовлено удовлетворяющим требованиям по надежности;

- ориентировочная, прогнозируемая оценка надежности сложного изделия на этапе отработки опытного образца для обоснования распределения требований к надежности частей изделия и обоснованного, хотя и ориентировочного, определения состава и количества запасных частей и сроков обслуживания.

Классификация:

1. Применительно к стадиям жизненного цикла систем различают расчеты на стадии проектирования (прогнозирующие расчеты) и на стадии эксплуатации и испытаний (главным образом - констатирующие расчеты). К первой относятся расчеты, основанные на анализе структуры системы и заданных условий работы. Их принято называть расчетноаналитическими или расчетами надежности. Ко второй - расчеты, связанные с обработкой результатов эксперимента или эксплуатации. Они называются - расчетноэкспериментальными или обработкой опытных, статистических данных.

2. По принципиальным основам расчеты делятся на элементные (системные) и функциональные (частным случаем которых являются расчеты параметрические).

3. По характеру учитываемых отказов различают расчеты с учетом одного вида отказов (внезапных, полных) и с учетом характеристик отказов (внезапные, постепенные, полные, частичные, типа замыкание, обрыв, сбои и т.д.).

4. По виду систем - расчеты простых систем (расчеты резервированных и не резервированных систем, систем без восстановления и с восстановлением) и сложных систем (расчеты надежности контуров управления и расчеты состояний систем).

Из приведенной классификации разработаны различные методы расчета надежности. Их развитие идет по пути разработки все новых моделей расчета. Реальные системы соответствуют модели расчета с некоторым коэффициентом подобия. Из приведенных в классификации расчетов надежности наиболее простыми и освоенными являются элементный, системный расчет с учетом одного вида отказов (внезапного, полного). К наиболее трудоемким отно-сятся функциональный расчет с учетом характера отказов (особенно сбоев), а также расчет надежности сложных и больших систем управления.

Методы расчетов

Для расчета надежности используются следующие основные методы:

- метод структурных схем;

- метод логических схем;

- схемно-функциональный метод;

- матричный метод;

- метод графов.

Метод структурных схем. Этот метод применяется для простых систем при следующих условиях:

- элементы систем рассматриваются как одноотказные;

- система представляется в виде единой структурной схемы, состоящей из суммы последовательных и параллельных соединений элементов, подсистем;

- в структурной схеме одно и тоже событие должно представляться в виде одного элемента, подсистемы, то есть должна соблюдаться ординарность.

Методика построения структурной схемы включает следующие основные этапы:

- составление на основе изучения конструкции функциональной системы принципиальной схемы системы;

- составление текстовой формулировки условий безотказности системы;

- составление структурной схемы, на которой прямоугольником обозначается событие безотказной работы элемента, а соединяющая линия обозначает связь - последовательность реализации событий безотказной работы системы в целом (последовательное или параллельное соединение);

- составляется уравнение для оценки вероятности безотказной работы системы.

Метод логических схем. Этот метод применяется:

- для систем, когда трудно обеспечиваются условия независимости событий и ординарности видов отказов, то есть для сложных функциональных систем

- систем с резервированием с дробной кратностью;

- систем с различными видами отказов для одних и тех же элементов;

- систем, выполняющих несколько функций.

Таким образом, сущность метода заключается в построении уравнения полной группы событий, характеризующих состояние работоспособности системы.

Порядок определения вероятности безотказной работы при методе логических схем следующий:

- формулируются условия безотказной работы системы в целом в зависимости от сочетания возможности появления отказов ее отдельных элементов;

- строится логическая схема условий безотказной работы системы с цепочкой логических связей ее работоспособности и возможных отказов отдельных элементов;

- составляется алгебраическое уравнение событий безотказной работы и расчетное уравнение вероятностей с использованием методов алгебры логики (алгебры Буля);

- производится подбор и подготовка количественных характеристик надежности элементов, входящих в систему;

- определяется вероятность безотказной работы системы в целом и отдельных ее частей.

В алгебре логики используются основные операции, обозначаемые символами "+" и "х". При логических операциях знак "+" имеет смысл"или". Например, запись А1 + А2означает, что имеет место событие А1 или событие А2. Знак "х" соответствует "и". Так, если запись А1хА2, то следует читать, что произошли или произойдут события А1 и А2.

Например, в системе, состоящую из двух параллельно включенных фильтров каждый фильтр (Ф1 и Ф2) может иметь по два отказа: отказ по засорению сеток q'ф и отказ по разрыву сеток q"ф, расчет надежности следует проводить методом логических схем.

1. Сформулируем условия безотказности (согласно порядку расчета).

Система будет работать безотказно, если:

а) все элементы работают безотказно;

б) произойдет отказ по засорению фильтра Ф1, при условии безотказной работы фильтра Ф2;

в) произойдет отказ по засорению фильтра Ф2, при условии безотказной работы фильтра Ф1.

Отказ по разрыву сеток фильтров считаем недопустимым, так как при этом не будет обеспечиваться очистка рабочей жидкости от механических примесей - грязное топливо пойдет в систему.

2. Составим логическую схему безотказной работы системы.

3. Составим алгебраическое уравнение события безотказности системы.

Отказ по разрыву сетки мы считаем недопустимым, но возможность его появления учитываем при помощи величины q"ф , в противном случае нельзя было бы пользоваться выражением для полной группы событий. Подставляем в уравнение для системы вероятности безотказной работы выраженные через вероятности появления отказа.

Теория графов.Раздел математики, имеющий широкое практическое применение. Здесь можно сформулировать большое количество задач, связанных развитием, проектированием и эксплуатацией дискретных объектов практически во всех областях науки и техники. Формирование направления оптимизации задач теория графов получило благодаря развитию ЭВМ.

Граф - форма записи комплекса, характеризуется двумя частями - отношением преобразования (преобразование энергии, переработка информации или массы с изменением свойств материала детали) и отношением связей.

Связь в комплексе - то, что объединяет функциональные элементы в одно целое, она всегда жесткая (не изменяется в процессе функционирования изделия, процесса). Через связь идет обмен веществом, энергией и информацией с окружающей средой, как между элементами, так и между объектами (изделиями).

Существует несколько способов задания графа - рисунком (вершины обозначаются точками, ребра, соединяющие эти точки, - линиями), матрицей инцидентности и матрицей смежности.

Граф состоит из множества х вершин и набора vпар вершин и обозначается G(x, v). Пара вершин, соединенных линиями, называется дугой или ребром графа. Ребро ориентировано - если есть стрелка, в противном случае он не ориентирован. Граф может быть смешанным.

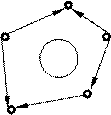
Граф 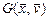- ориентирован, если порядок концевых вершин существенен и состоит из ориентированных ребер (рис. 1.2, а). Граф G(x,v) - неориентирован, если порядок концевых вершин несущественен и состоит из неопределенных ребер (рис. 1.2, б). Граф 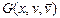- смешанный и содержит ориентированные и неориентированные ребра (рис. 1.2, в).

Последовательность ребер Е, в которой два соседних ребра имеют общую вершину, называется маршрутом W.

Произвольный граф G(x, v), где 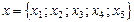; 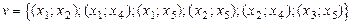показан на рис. 1.2, б.

Если задано множество вершин х и соответствие Т, составляющее каждой вершине хÎХ графа множество вершин Т_х, связанных с ней ребрами, то определен граф G=(XT). Для графа (рис. 1.2, б)

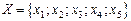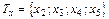, а , (1.1)

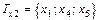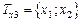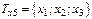, , . (1.2)

Рис. 1.2. Типы графов:

а - ориентированный; б – неориентированный; в - смешанный

Полюсный граф одномерных элементов - ориентированный граф из одномерных элементов, является универсальной моделью информационных комплексов с сосредоточенными компонентами различной физической природы: электрической, механической, тепловой и др. (рис. 1.3).

Полюсный граф строится таким образом, чтобы обеспечивались наиболее простые отношения между его структурой и уравнениями связи. Они формируются:

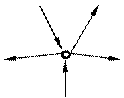
1. Алгебраическая сумма поперечных переменных для любой вершины графа равна нулю - Sh(t)=0 (рис. 1.4, а);

2. Алгебраическая сумма продольных переменных для любого контура графа равна нулю - Sx (t)=0 (рис. 1.4, б).

а)

б)

Рис. 1.3. Одномерный элемент и его полюсный граф

При алгебраическом суммировании переменных они считаются положительными, если их направления совпадают с выбранным направлением относительно вершины или контура, и отрицательными, если направления переменных противоположны выбранным направлениям.

h₂ h₃ x₁ x₂

h₄

h₁ x₅ x₃

h₅

x₄

h₁-h₂+h₃+h₄-h₅=0 x₁-x₂+x₃+x₄-x₅=0

а) б)

Рис. 1.4. Уравнение связей для вершин (а) и контура (б)

Полюсный граф многомерных элементов. Многомерный элемент, имеющий т+1 векторных величин, посредством которых он может объединятся с другими элементами, характеризуется т независимыми поперечными переменными h₁; h_2; ...; h_т и т независимыми продольными переменными x₁; x₂;...;x_т .

Уравнения, записанные относительно поперечных переменных:

,

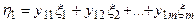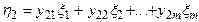, (1.3)

,

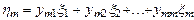или в матричной форме ,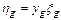

где 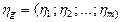- вектор поперечных переменных;

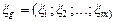- вектор продольных переменных;

y_g - квадратичная матрица т-го порядка.

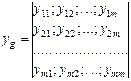. (1.4)

Например, любую структуру механико-технической системы обычно рассматривают в терминах теории графов, т.е. в виде ориентированного графа, вершины которого соответствуют аппаратам, а дуги – потокам (рис. 1.5), номера вершин обозначены курсивом (справа сверху от вершины), а номера потоков – малым прямым шрифтом (под линией соответствующего потока).

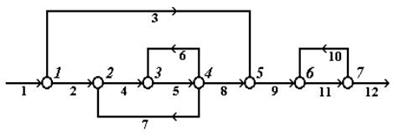
Рис. 1.5. Представление механико-технической системы в виде ориентированного графа

Последовательность сцепленных дуг, позволяющая пройти от одной вершины к другой, называется путем. Путь можно обозначить как через последовательность дуг, так и через последовательность вершин. Путь, начальная вершина которого совпадает с конечной, причем каждая вершина, за исключением начальной, проходится только один раз, называется контуром. Например, на рис. 1.5 имеются три контура (по вершинам): 2-3-4-2, 3-4-3 и 6-7-6.

Комплексом, называется часть графа, вершины которого обладают следующими свойствами:

- каждая из вершин и дуг комплекса входит в один из контуров графа;

- если вершина i входит в комплекс, то в этот комплекс входят также все вершины, входящие в контуры, которые содержат вершину i.

Например, на графе, представленном на рис. 1.5, имеются два комплекса (по вершинам): 2-3-4 и 6-7. В первый комплекс входят два контура (2-3-4-2 и 3-4-3), а во второй – один (6-7-6).