Логарифмические неравенства
Решение логарифмических неравенств основано на том, что функция 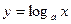 при a>1 является монотонно возрастающей, а при 0<a<1 – монотонно убывающей.
при a>1 является монотонно возрастающей, а при 0<a<1 – монотонно убывающей.
1. При переходе от простейших логарифмических неравенств к равносильным системам неравенств, не содержащим знака логарифма, следует учитывать область допустимых значений исходного неравенства.
Простейшие логарифмические неравенства:
1. 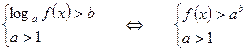 2.
2. 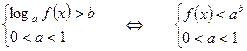
3. 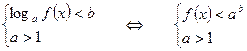 4.
4. 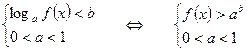
Пример 1. Решите неравенство 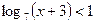 .
.
Решение. Находим область допустимых значений (ОДЗ): 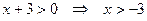 .
.
Неравенство 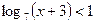 является простейшим логарифмическим неравенством, следовательно, имеет решение:
является простейшим логарифмическим неравенством, следовательно, имеет решение: 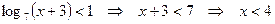
 Находим пересечение полученного интервала с ОДЗ, получаем
Находим пересечение полученного интервала с ОДЗ, получаем 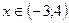 .
.
Пример 2. Найдите область определения функции 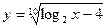 .
.
Решение. Область определения функции удовлетворяет условию существования корня чётной степени и условию существования логарифма и определяется из системы:
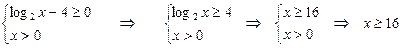
2. Логарифмическое неравенство вида 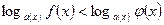 эквивалентно совокупности двух систем неравенств:
эквивалентно совокупности двух систем неравенств:
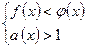 или
или 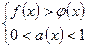
Пример 3. Решите неравенство 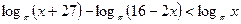 .
.
Решение. Находим ОДЗ из системы неравенств:
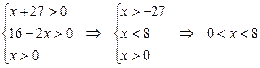 .
.
Представим данное неравенство в виде:
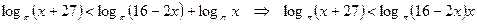 .
.
Так как основание логарифма 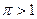 , то знак неравенства не меняется:
, то знак неравенства не меняется:
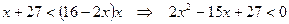 .
.
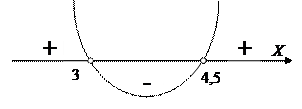 Корни соответствующего квадратного уравнения
Корни соответствующего квадратного уравнения 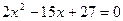 равны
равны 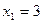 и
и 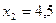 . Находим решение квадратного неравенства. Решением квадратного неравенства является интервал
. Находим решение квадратного неравенства. Решением квадратного неравенства является интервал 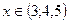 . С учётом ОДЗ получаем ответ
. С учётом ОДЗ получаем ответ 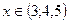 .
.
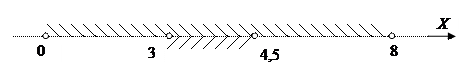
Пример 4. Решите неравенство 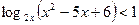 .
.
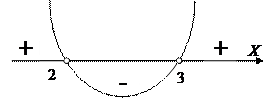 Решение. Область допустимых значений удовлетворяет условиям
Решение. Область допустимых значений удовлетворяет условиям 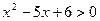 ,
, 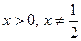 . Для решения квадратного неравенства
. Для решения квадратного неравенства 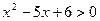 находим корни квадратного уравнения
находим корни квадратного уравнения 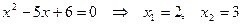 . Определяем знаки квадратного трёхчлена
. Определяем знаки квадратного трёхчлена 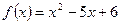 . Решением квадратного неравенства является объединение интервалов
. Решением квадратного неравенства является объединение интервалов 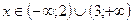 . ОДЗ находим из системы неравенств:
. ОДЗ находим из системы неравенств:
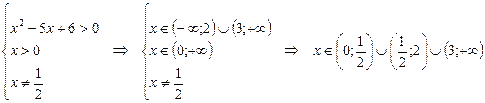
Решение неравенства 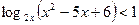 , т.е.
, т.е. 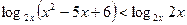 сводится к рассмотрению двух случаев.
сводится к рассмотрению двух случаев.
 1) Если 2x>1, т.е.
1) Если 2x>1, т.е. 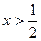 , то
, то 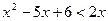 . Решаем квадратное неравенство
. Решаем квадратное неравенство 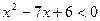 . Корни квадратного уравнения
. Корни квадратного уравнения 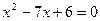 равны
равны 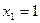 и
и 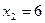 . Определяем знаки функции
. Определяем знаки функции 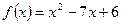 . Решением квадратного неравенства является
. Решением квадратного неравенства является 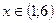 . Получаем:
. Получаем:
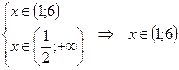 .
.
2) Если 0<2x<1, т.е. 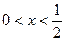 , то
, то 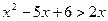 . Решаем квадратное неравенство
. Решаем квадратное неравенство 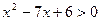 . Решением квадратного неравенства является объединение интервалов
. Решением квадратного неравенства является объединение интервалов 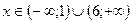 . Получаем:
. Получаем: 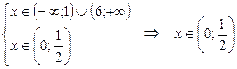 .
.
Объединяем первый и второй случаи 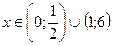 . С учётом ОДЗ получаем
. С учётом ОДЗ получаем 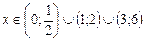 .
.
Пример 5. Решите неравенство 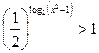 .
.
Решение. ОДЗ удовлетворяет условию 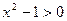 , решаем соответствующее квадратное уравнение
, решаем соответствующее квадратное уравнение 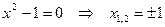 и определяем знаки функции
и определяем знаки функции 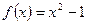 , ОДЗ:
, ОДЗ: 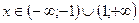 . При решении неравенства
. При решении неравенства 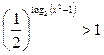 используем основное логарифмическое тождество
используем основное логарифмическое тождество 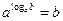 :
:
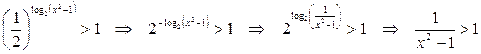 .
.
Решаем полученное неравенство методом интервалов:
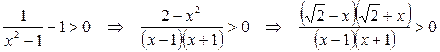 .
.
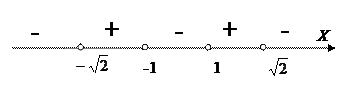 Решением неравенства
Решением неравенства 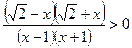 является объединение интервалов
является объединение интервалов 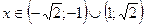 . С учётом ОДЗ получаем
. С учётом ОДЗ получаем 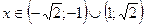 .
.
Пример 6. Решите неравенство 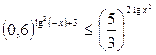 .
.
Решение. ОДЗ: 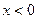
Приводим обе части неравенства к одному основанию 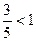 :
:
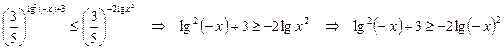 .
.
Получаем 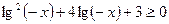 , с помощью замены переменной
, с помощью замены переменной 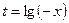 приводим данное неравенство к квадратному
приводим данное неравенство к квадратному 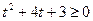 . Корни соответствующего квадратного уравнения
. Корни соответствующего квадратного уравнения 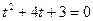 равны
равны 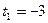 и
и 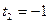 . Находим решение квадратного неравенства.
. Находим решение квадратного неравенства.
 Решением квадратного неравенства является
Решением квадратного неравенства является 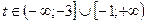 . Делаем обратную замену и получаем совокупность неравенств:
. Делаем обратную замену и получаем совокупность неравенств:
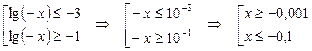
Таким образом, 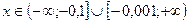 . С учётом ОДЗ решением неравенства является множество
. С учётом ОДЗ решением неравенства является множество 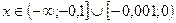 .
.
Ответ: 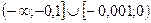 .
.
Пример 7.Найдите все значения x, при которых точки графика функции 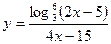 лежат ниже соответствующих точек графика функции
лежат ниже соответствующих точек графика функции 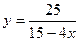 .
.
Решение. Согласно условию задачи получаем неравенство:
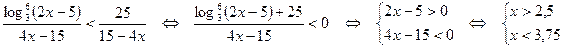
Ответ: 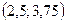 .
.
Задачи.
1. Решите неравенства:
1) 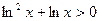 2)
2) 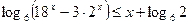
3) 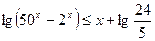 4)
4) 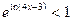
5) 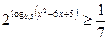 6)
6) 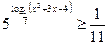
7) 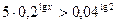 8)
8) 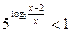
2. Решите неравенство 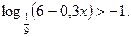
1) 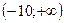 2)
2) 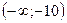 3) (-10;20) 4) (-10;20)
3) (-10;20) 4) (-10;20)
3. Решите неравенство 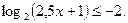
4. Наибольшее целое решение неравенства 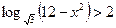 равно
равно
1) 1
5) 3
9) 6
2) -1
6) -3
10) -6
3) 2
7) 5
11) 0
4) -2
8) 4
12)-5
5. Решите неравенство 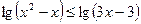 .
.
6. Решите неравенство 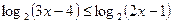 .
.
7. Решите неравенство 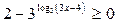 .
.
8. Наибольшее целое решение неравенства 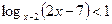 равно
равно
1) 9
5) 10
9) 18
2) 8
6) 14
10) 11
3) 6
7) 16
11) 20
4) 4
8) 12
12) 3
9. Число целых решений неравенства 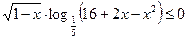 равно
равно
1) 1
5) 5
2) 2
6) 6
3) 3
7) 7
4) 4
8) 0
10. Найдите число целых решений неравенства 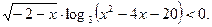
11. Найдите сумму целых решений неравенства 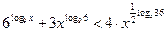 .
.
12. Найдите область определения функции 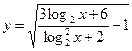 .
.
13. Найдите область определения функции 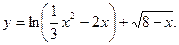
14. Найдите область определения функции 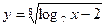 .
.
1) 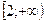 2)
2) 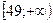 3)
3) 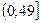 4)
4) 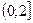
15. Найдите область определения функции 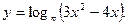
16. Найдите область определения функции 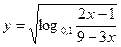
17. Найдите область определения функции 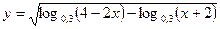 .
.
1) 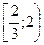 2)
2) 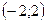 3)
3) 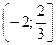 4)
4) 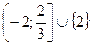
18. Найдите все значения x, при которых точки графика функции 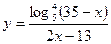 лежат ниже соответствующих точек графика функции
лежат ниже соответствующих точек графика функции 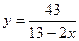 .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| Производительность ВС. | | | Эксплуатация песколовок |
Дата добавления: 2020-05-20; просмотров: 507;











