Логарифмические частотные характеристики динамических звеньев и систем

Логарифмическая амплитудно-частотная характеристика (логарифмическая амплитудная характеристика, ЛАХ) L(w) определяется путем преобразования амплитудно-частотной характеристики (АЧХ) A(w):

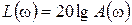
и имеет единицу измерения – децибел (дБ).

Для логарифмической фазо-частотной характеристики (ЛФЧХ, ЛФХ) используется выражение j(w), полученное для обычной фазо-частотной характеристики (ФЧХ).

Очевидно, ЛАХ и ЛФЧХ не содержат новой информации по сравнению с АЧХ и ФЧХ. Целесообразность их получения и использования полностью определяется особыми правилами их построения, предоставляющими широкие возможности для построения удобных и наглядных процедур анализа и синтеза систем управления. Аппарат ЛАХ и ЛФЧХ является основой классической теории линейных непрерывных и дискретных систем.

Необходимо отчетливо представлять себе необходимость точного соблюдения правил построения ЛАХ и ЛФЧХ, так как без этого рассматриваемые характеристики теряют смысл, и их применение с нарушением правил построения приводит к неверным результатам.

При построении рассматриваемых характеристик для горизонтальной оси (оси частот) используется логарифмический масштаб (рисунок 62), то есть положение конкретных частот на оси соответствует значениям их десятичных логарифмов. Другими словами, в обычном линейном масштабе по горизонтальной оси откладываются не сами частоты w, а значения lg w. Угловая частота, как и обычно, измеряется в 1/с (рад/с), но в силу применяемого масштаба единицей измерения по оси абсцисс является декада (определение приводится ниже).

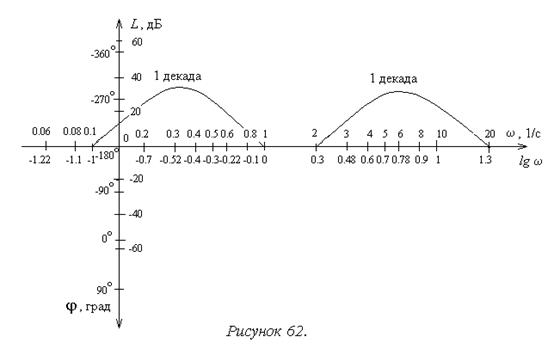
На рисунке 62 выше горизонтальной оси указаны значения частот, ниже оси – их десятичных логарифмов.

Отметим следующие обстоятельства, характерные для используемого логарифмического масштаба:

1. Отрицательные частоты не рассматриваются.

2. Отметка частоты w=0 на оси отсутствует. При w®0 lg w® -¥, и соответствующие отметки частоты смещаются по горизонтальной оси влево в бесконечность.

3. Вертикальная ось проводится через отметку частоты, соответствующую нижней границе диапазона существенных частот для изображаемых характеристик.

4. Изменению значения частоты в k раз соответствует отрезок оси постоянной длины независимо от его расположения на оси (то есть абсолютных значений частот).

5. Отрезок горизонтальной оси, соответствующий десятикратному изменению частоты, называется декадой. Длина декады, очевидно, постоянна независимо от ее расположения на оси.

На вертикальной оси откладываются в линейном масштабе значения L(w) в децибелах. С горизонтальной осью совмещается отметка 0 дБ.

Логарифмическая фазо-частотная характеристика строится совместно с ЛАХ, причем горизонтальная ось у обеих характеристик полностью совпадает, а вертикальная ось для ЛФЧХ совмещается с вертикальной осью ЛАХ следующим образом:

1. Направление положительного отсчета значений ЛФЧХ – вниз.

2. С отметкой 0 дБ для ЛАХ (пересечение с горизонтальной осью) совмещается отметка -180° для ЛФЧХ.

Рассмотрим некоторые примеры построения логарифмических характеристик, позволяющие обнаружить основные закономерности их формирования.

1. Безынерционное звено:

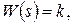
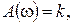
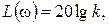
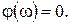
Характеристики показаны на рисунке 63а.

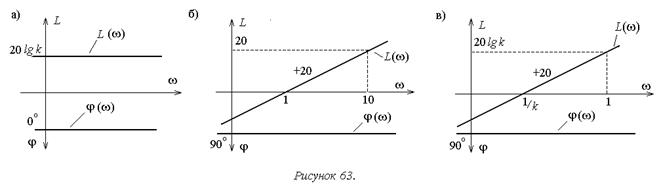
2. Идеальное дифференцирующее звено (k=1):

, ,

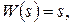
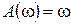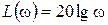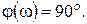
Поскольку вдоль горизонтальной оси используется линейный масштаб для lgw, график L(w) будет представлять собой прямую линию (рисунок 63б). Ее наклон принято измерять в децибелах на декаду (дБ/дек). В рассматриваемом примере при увеличении w в 10 раз, то есть на одну декаду, L(w) получит приращение

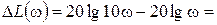
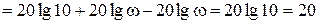дБ.

Поэтому наклон ЛАХ здесь составляет +20 дБ/дек.

При w=1 здесь lgw=0, и ЛАХ пересечет горизонтальную ось.

3. Идеальное дифференцирующее звено (общий случай):

,

, ,

.

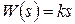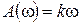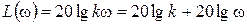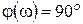ЛАХ также будет представлять собой прямую с наклоном +20 дБ/дек и по сравнению с предыдущим примером будет проходить на 20lgk децибел выше (рисунок 63в).

Точка пересечения ЛАХ с горизонтальной осью может быть найдена из условия:

,

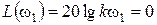откуда , .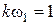

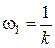При w=1 значение ЛАХ составит L(1)=20lgk.

4. Звено с передаточной функцией :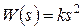

, ,

.

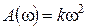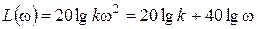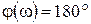ЛАХ остается прямой линией, но ее наклон по сравнению с предыдущим случаем увеличится в два раза (рисунок 64а).

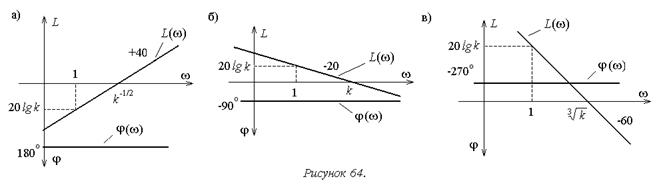
ЛАХ пересекает горизонтальную ось при , .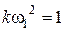

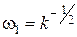При w=1 L(1)=20lgk.

5. Идеальное интегрирующее звено:

,

, ,

.

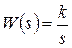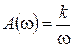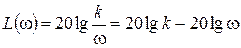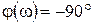ЛАХ остается прямой линией (рисунок 64б). Ее приращение при изменении частоты в 10 раз составит:

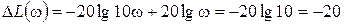дБ.

Наклон ЛАХ –20дБ/дек.

Точка пересечения ЛАХ с горизонтальной осью может быть найдена из условия:

,

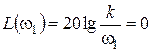откуда w₁=k.

6. Звено с передаточной функцией :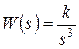

, ,

.

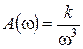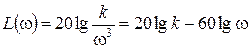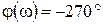ЛАХ – прямая линия, но ее наклон по сравнению с предыдущим примером увеличится в 3 раза и составит –60 дБ/дек (рисунок 64в).

Точка пересечения ЛАХ с горизонтальной осью: , .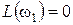

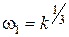При w=1 L(1)=20lgk.

Нетрудно убедиться, что в общем случае для идеальных звеньев с передаточной функцией вида 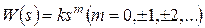ЛАХ является прямой с наклоном 20m дБ/дек и пересекает горизонтальную ось на частоте 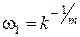. При w=1 значение ЛАХ составляет 20lgk. ЛФЧХ является горизонтальной прямой и проходит на уровне 90.m°.

Для последующих примеров построение точных логарифмических характеристик возможно только на основе численного расчета, что не вызывает труда при использовании компьютера и программных средств типа MATLAB. Однако для решения практических задач большое значение имеют приемы их приближенного построения и прежде всего – построение асимптотической ЛАХ.

7. Звено с передаточной функцией W(s)=Ts+1:

,

, ,

.

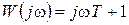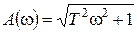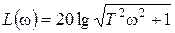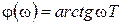Графики точных логарифмических характеристик показаны на рисунке 65а.

Асимптотическая ЛАХ может быть построена исходя из следующих соображений.

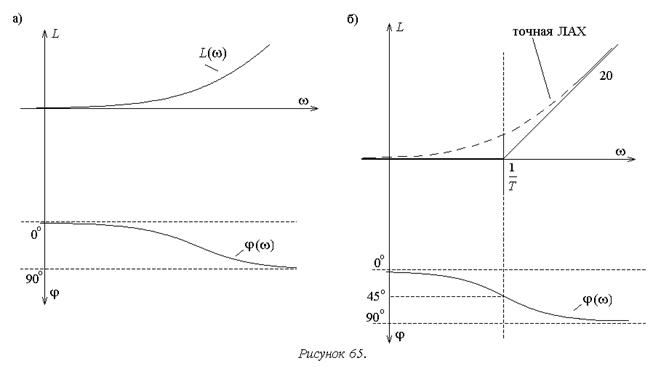
Вводится сопрягающая частота w_с, исходя из условия равенства двух слагаемых, расположенных под корнем в выражении для ЛАХ: слагаемого, содержащего низшую степень частоты и слагаемого, содержащего высшую степень частоты. Для рассматриваемого примера получим:

, .

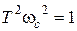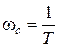Далее рассматриваются два диапазона частот.

Для низких частот, определяемых условием w<<w_с, будет иметь место Tw<<1, и выражение для ЛАХ приближенно примет вид:

.

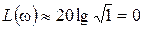Соответствующий этому выражению график – прямая, совпадающая с левой частью горизонтальной оси, является асимптотой точной ЛАХ при w®0 (рисунок 65б).

Для высоких частот, определяемых условием w>>w_с, будет иметь место Tw>>1, и выражение для ЛАХ приближенно примет вид:

.

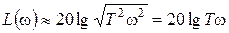Нетрудно убедиться, что график этого выражения будет представлять собой прямую с наклоном +20дБ/дек. Эта прямая является асимптотой точной ЛАХ при w®¥. Она пересечет горизонтальную ось на частоте w₁=1/T, то есть асимптоты точной ЛАХ пересекаются на сопрягающей частоте.

Асимптотической ЛАХ называется ломаная линия, состоящая из отрезков асимптот точной ЛАХ. Абсолютная величина погрешности асимптотической ЛАХ по отношению к точной в рассматриваемом примере достигает максимума на сопрягающей частоте и составляет:

.

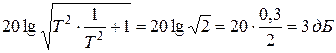По мере удаления от сопрягающей частоты влево или вправо погрешность снижается и на расстоянии 0,3 декады от сопрягающей частоты уменьшится примерно в 3 раза, на расстоянии 0,5 декады от сопрягающей частоты – более, чем в 7 раз, а на расстоянии более декады от сопрягающей частоты будет пренебрежимо мала.

Отметим также некоторые свойства графика ЛФЧХ, соответствующего выражению arctgwT. Так как данное выражение входит в состав выражений для ЛФЧХ большинства более сложных звеньев и систем, эти свойства могут быть использованы для их приближенного анализа.

При w®0 асимптотой графика ЛФЧХ является горизонтальная прямая, проходящая через отметку 0°. При w®¥ асимптота – горизонтальная прямая, проходящая через отметку 90°.

На сопрягающей частоте 1/T значение ЛФЧХ составляет 45°. Эта точка является центром симметрии всего графика (рисунок 65б).

8. Апериодическое звено 1-го порядка:

,

,

,

.

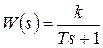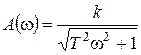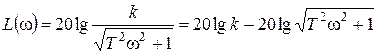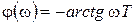Примем сначала k=1. Рассмотрев, аналогично предыдущему примеру, низкие и высокие частоты, разделенные их сопрягающей частотой w_с=1/T, нетрудно получить асимптотическую ЛАХ. Единственное отличие от предыдущего примера будет состоять в противоположном наклоне второго участка. Он составит –20 дБ/дек (рисунок 66а).

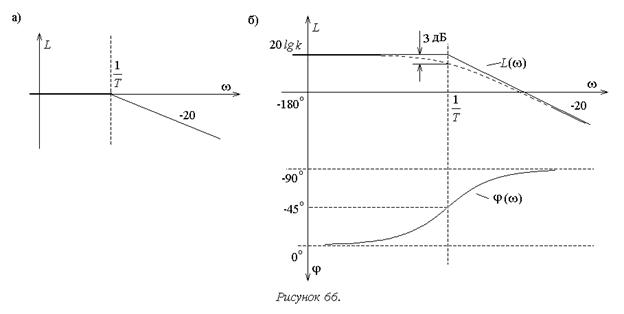
При k¹1 весь график сместится вверх при k>1 (20lgk>0), а при k<1 – вниз (20lgk <0). Оценка погрешности асимптотической ЛАХ по отношению к точной аналогична полученной в предыдущем примере.

Все результаты, полученные для ЛФЧХ, также сохраняются с учетом смены знака (рисунок 66б).

В общем случае для звена с передаточной функцией W(s)=k(Ts+1)^m, где m=0, ±1, ±2, … получим следующие соотношения:

,

,

.

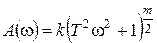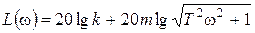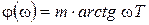Отметим следующие закономерности:

- величина сопрягающей частоты, разделяющей участки асимптотической ЛАХ, w_с=1/T,

- первый участок асимптотической ЛАХ горизонтален и проходит на уровне 20lgk,

- наклон второго участка 20.m дБ/дек,

- абсолютная величина погрешности асимптотической ЛАХ по отношению к точной максимальна по сопрягающей частоте и составляет 3.m дБ,

- значение ЛФЧХ монотонно изменяется от 0° (при w®0) до 90°×m (при w®¥); на сопрягающей частоте ее значение составляет 45°×m; эта точка является точкой симметрии всего графика ЛФЧХ.

9. Колебательное звено:

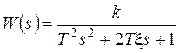, 0< x<1,

,

,

,

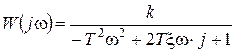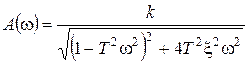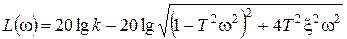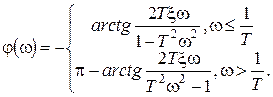
Рассмотрим построение асимптотической ЛАХ.

Под корнем в выражении для ЛАХ здесь присутствуют несколько слагаемых. Тем не менее, принцип построения сохраняется. Сопрягающая частота находится из условия равенства двух слагаемых – содержащих низшую и высшую степень частоты:

, .

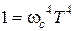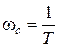На низких частотах, w<<1/T, всеми слагаемыми, содержащими произведение wT, можно пренебречь по сравнению с единицей (wT<<1). В результате выражение для ЛАХ приближенно примет вид:

.

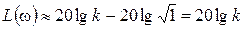Это уравнение горизонтальной прямой – асимптоты точной ЛАХ при w®0.

На высоких частотах, w>>1/T, под корнем можно пренебречь всеми слагаемыми, кроме содержащего высшую степень частоты. Выражение для ЛАХ приближенно примет вид:

.

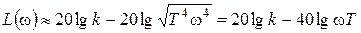Это выражение для прямой с наклоном –40дБ/дек, причем при wT=1, то есть на сопрягающей частоте она проходит через точку с вертикальной координатой 20lgk. Эта прямая является асимптотой точной ЛАХ при w®¥. Здесь, как и в предыдущих примерах, асимптоты ЛАХ пересекаются на сопрягающей частоте (рисунок 67а), что является общим правилом.

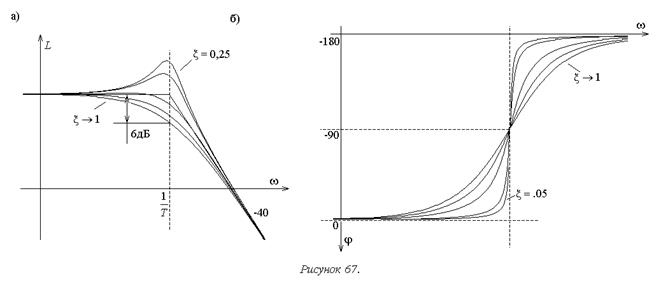
Закономерность формирования погрешностей асимптотической ЛАХ для колебательного звена является более сложной, чем в предыдущих примерах.

Прежде всего, оценим величину этой погрешности на сопрягающей частоте. Для асимптотической ЛАХ получим:

.

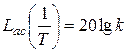Для точной ЛАХ:

.

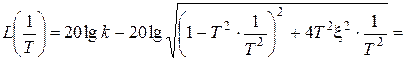
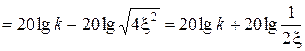Величина погрешности 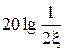зависит от величины x и изменяется от –6 дБ при x®1 до сколь угодно больших положительных значений при x®0.

Этот эффект обусловлен резонансными свойствами колебательного звена и в общем случае не позволяет при его анализе ограничиваться использованием только асимптотической ЛАХ.

Точные ЛАХ колебательного звена для различных значений x показаны на рисунке 67а. По ним видно, что резонансная частота, доставляющая максимум ЛАХ, отличается от сопрягающей. Резонансная частота w_р может быть найдена из условия:

.

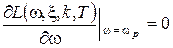Общие рекомендации по использованию асимптотической ЛАХ для рассматриваемого примера сводятся к следующему:

- при больших значениях x, когда резонансный пик отсутствует или не превышает величины 3дБ, допустимо использование асимптотической ЛАХ;

- при малых x, когда высота резонансного пика превышает 3дБ, должна использоваться точная ЛАХ.

ЛФЧХ для различных x показаны на рисунке 67б.

Рассмотрим правила построения асимптотических ЛАХ для более сложных передаточных функций на следующем примере:

,

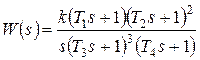где k=40с^-2, T₁=0,5с, T₂=2,5с, T₃=20с, T₄=0,01с.

Выражения для АЧХ и точной ЛАХ будут иметь вид:

,

.

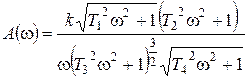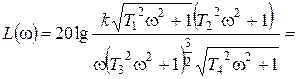
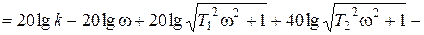
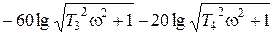Наиболее распространенная в литературе рекомендация сводится к рассмотрению выражения для ЛАХ сложного звена как суммы выражений для ЛАХ рассмотренных выше звеньев, каждому из которых соответствует максимум одна сопрягающая частота. Асимптотические ЛАХ этих звеньев представляют собой линейные (для первых двух слагаемых) или кусочно-линейные (для остальных слагаемых) характеристики, состоящие из низкочастотной асимптоты, совпадающей с горизонтальной осью, и высокочастотной асимптоты с соответствующим наклоном, пересекающихся на сопрягающей частоте. Если общее выражение для ЛАХ записывать так, чтобы в отдельных слагаемых под знаком логарифма оставались выражения вида 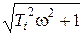, то наклоны таких асимптот будут совпадать по величине с коэффициентами при 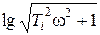. Результирующий график асимптотической ЛАХ может быть получен сложением графиков отдельных слагаемых.

Более удобным является предлагаемый ниже способ (при сохранении сформулированного правила записи выражения для ЛАХ). Он состоит в следующей последовательности действий.

1. Определяются сопрягающие частоты, соответствующие отдельным слагаемым, и записываются в порядке возрастания:

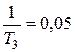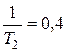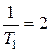с^-1; с^-1; 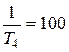с^-1; с^-1.

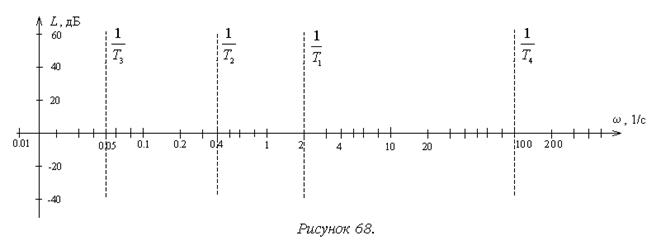
2. Выбирается масштаб для оси частот так, чтобы крайние сопрягающие частоты располагались на расстоянии от 0,5 до 1 декады от краев видимой горизонтальной оси. Через сопрягающие частоты проводятся вертикальные пунктирные прямые (рисунок 68). Пунктирные прямые делят все поле графика на зоны, которым соответствуют отрезки различных асимптот ЛАХ (участки асимптотических ЛАХ). Построение асимптотической ЛАХ далее выполняется последовательно по участкам, начиная с первого.

3. Первый участок расположен левее всех сопрягающих частот. Следовательно, его уравнение, получаемое по условию w<<1/T_i (i=1,2,3,4), будет иметь вид:

.

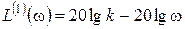Это уравнение прямой с наклоном –20 дБ/дек. Для ее построения необходимо найти опорные точки. Например:

- w=1 с^-1: L⁽¹⁾(1)=20lgk=20lg40=32 дБ;

- w=0,1 с^-1: L⁽¹⁾(0,1)=20lg40-20lg0,1=32+20=52 дБ.

В качестве опорной может также использоваться точка пересечения данной прямой с горизонтальной осью, координаты которой могут быть найдены из условия L⁽¹⁾(w₁)=0:

,

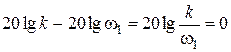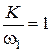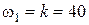, с^-1.

Для последующего построения потребуется также точка пересечения первого участка асимптотической ЛАХ с границей участка. Ее координаты: 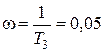с^-1, L⁽¹⁾(0,05)=20lg40-20lg0,05=32+26=58 дБ.

Отрезок асимптотической ЛАХ, выходящий за пределы соответствующего участка, показывают пунктирной линией (рисунок 69).

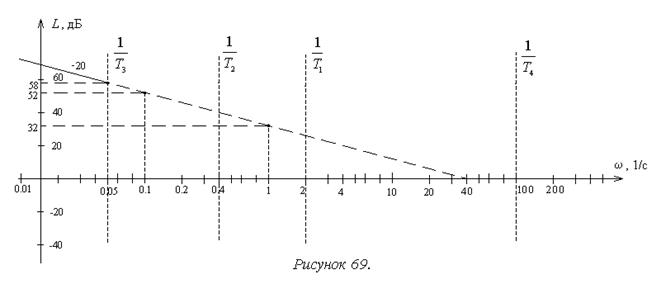
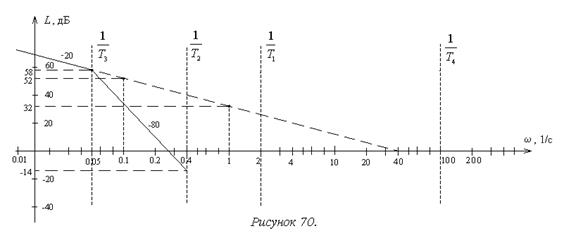
4. Второй участок расположен правее сопрягающей частоты 1/T₃, которой в выражении для ЛАХ соответствует коэффициент –60. По аналогии с рассмотренными выше примерами 7-9 можно придти к выводу, что наклон второго участка по сравнению с первым изменится на величину –60 дБ/дек и составит –80 дБ/дек (рисунок 70). Координата левой границы участка получена выше: (0,05 с^-1; 58 дБ). Длина участка вдоль горизонтальной оси в соответствии с используемым логарифмическим масштабом составляет 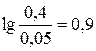декады. Следовательно, асимптотическая ЛАХ на данном участке получит приращение:

–80 дБ/дек ´ 0,9 дек = –72 дБ,

и координаты правой границы участка будут равны:

w=0,4 с^-1; L⁽²⁾(0,4)=58 –72= –14 дБ.

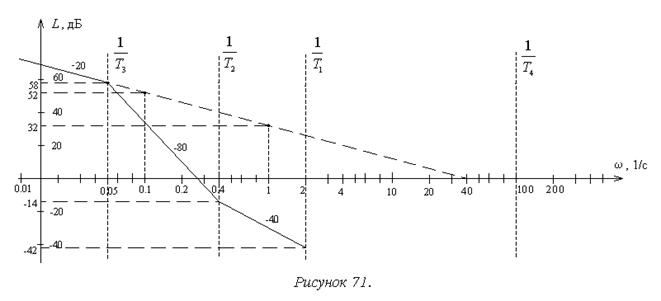
5. Третий участок разделен со вторым сопрягающей частотой 1/T₂. Дополнительный наклон по отношению ко второму участку равен +40 дБ/дек (рисунок 71). Следовательно, наклон участка составит –40 дБ/дек. Длина участка 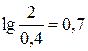декады, координаты правой границы:

w=2 с^-1 и L⁽³⁾(2)= –14 – 40дБ/дек ´ 0,7дек= –42 дБ.

6. Четвертый участок разделен со третьим сопрягающей частотой 1/T₁. Дополнительный наклон по отношению к третьему участку равен +20 дБ/дек (рисунок 72). Следовательно, наклон участка составит –20 дБ/дек. Длина участка 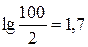декады, координаты правой границы:

w=100 с^-1 и L⁽⁴⁾(100)= –42 – 20´1,7= –76 дБ.

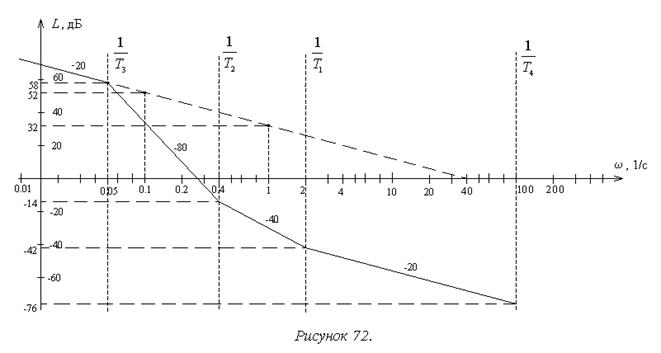
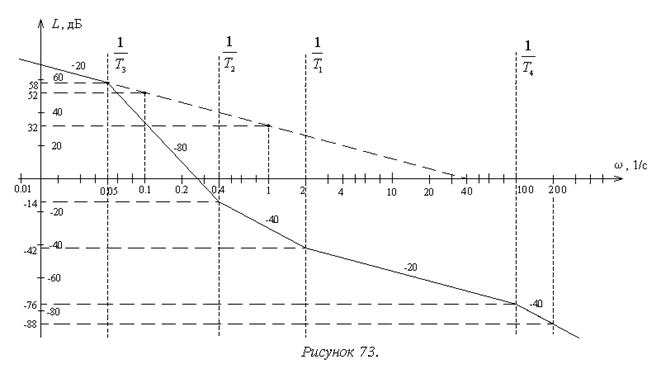
7. Пятый участок разделен со четвертым сопрягающей частотой 1/T₄. Дополнительный наклон по отношению к четвертому участку равен –20 дБ/дек. Следовательно, наклон участка составит –40 дБ/дек. Для его построения необходимо рассчитать в дополнение к начальной еще одну его точку на любой частоте, например: w=200 с^-1 и L⁽⁵⁾(200)= –76 – 40´0,3= –88 дБ.

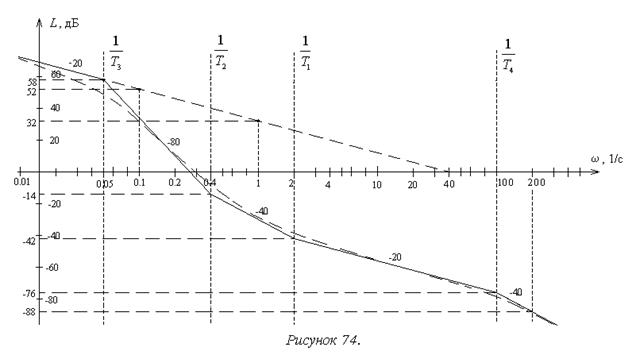
Результирующая асимптотическая ЛАХ показана на рисунке 73.

Пунктиром на рисунке 74 добавлена точная ЛАХ для рассматриваемого примера. Сопрягающие частоты 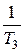и 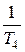удалены от ближайших к ним сопрягающих частот на расстояние более 0,7 декады. Поэтому на этих частотах погрешности равны соответственно 9 и 3 Дб. В окрестности сопрягающих частот 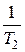и 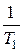их взаимное влияние приводит к некоторому увеличению погрешности.