Константа локализации элементарных частиц

Произведение массы 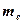электрона на его радиус 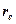- величина постоянная, названная нами константой локализации элементарных частиц. Она едина у фотона 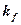, электрона 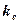, протона 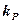и нейтрона .

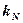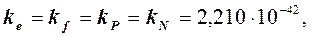(39)

Таким образом, константа локализации электрона равна

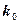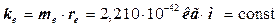= . (40)

Из этого следует теоретическая величина радиуса электрона 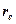(рис. 39)

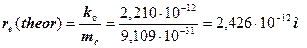. (41)

Если масса свободного электрона постоянна 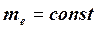, то и радиус его тоже постоянен .

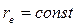Приведённая информация даёт нам основания представить электрон в первом приближении в виде кольца (рис. 39, а). Вполне естественно, что сразу же возникает необходимость определения радиуса 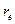кольца электрона не только теоретически (41), но и экспериментально.

Поскольку 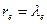, то имеется возможность сравнить теоретическую величину радиуса 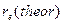(41) с экспериментальной длиной волны электрона, определённой Комптоном. Он нашёл эмпирическую формулу для расчета изменения длины волны 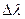рентгеновского фотона, отражённого от электрона

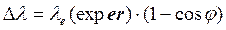. (42)

В этой формуле величина 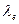выполняет роль экспериментального коэффициента, который он назвал длиной волны электрона. Она оказалась равной теоретическому радиусу электрона (41)

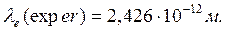(43)

Совпадение теоретической величины 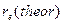(41) радиуса электрона и экспериментальной величины длины его волны 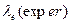(43) служит веским доказательством справедливости равенства .

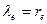Угловую скорость 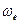вращения кольца электрона определим, используя постоянную Планка, которая для электрона записывается так

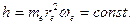(44)

Отсюда имеем

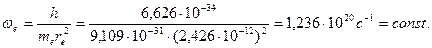(45)

Скорость 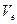точек вращающегося базового кольца электрона (рис. 39, а) равна скорости света .

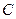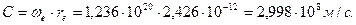(46)

Чтобы получить математические модели, содержащие другие характеристики электрона, надо детально проанализировать силы, действующие на вращающееся кольцо.

Известно, что электрон имеет собственную энергию, которую обычно определяют по формуле 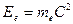. Однако смысл такого допущения не всегда расшифровывается. А он заключается в том, что если всю массу электрона перевести в массу фотона, то энергия электрона будет равна 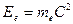. Этот факт имеет экспериментальное подтверждение. Известно, что массы электрона и позитрона равны. Взаимодействуя друг с другом, они образуют два фотона. Вот почему мы можем приписать электрону энергию, равную энергии фотона, имеющего соответствующую массу. Энергию электрона 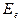, равную энергии фотона, назовем фотонной 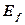энергией электрона.

А теперь исследуем возможности кольцевой модели свободного электрона (рис. 39, а) [1], [3]. Для этого предполагаем, что электрон имеет равные между собой кинетическую 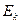и потенциальную 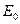энергии, сумма которых равна его фотонной энергии .

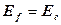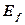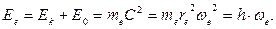= (47)

Расчет по этой формуле дает такое значение фотонной энергии электрона

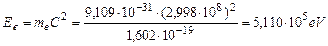. (48)

Если свободный электрон вращается только относительно своей оси, то угловая частота 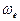вращения кольцевой модели свободного электрона, определенная из формулы (47), оказывается равной [1], [3].

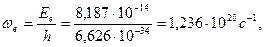(49)

а теоретический радиус кольца электрона 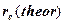оказывается равным его экспериментальной величине (43)

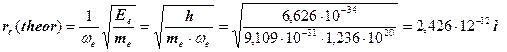. (50)

Как видно, теоретические величины радиуса кольца электрона, определённые по формулам (41), (50) и (51) равны экспериментальному значению комптоновской длины волны электрона 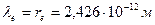(43).

Другая совокупность параметров электрона даёт тот же научный результат 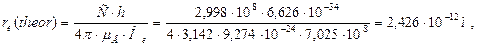(51).

(51)

где 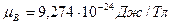- магнетон Бора; 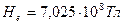- напряженность магнитного поля в центре симметрии электрона.

Итак, главный параметр кольцевой модели свободного электрона - радиус кольца 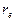, определённый по формулам (41), (50) и (51), оказался одинаковым и равным комптоновской экспериментальной величине длины волны 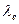электрона (43) [1], [3].

Во втором приближении к реальности модель электрона (рис. 39, b) можно представить с двумя вращениями: относительно центральной оси кольца и относительно кольцевой оси тора (рис. 39, b). Это - полый тор, вращающийся относительно центральной оси и относительно кольцевой оси тора (рис. 39, b). В результате получается, что электрон - элементарная частица с двумя вращениями. Она оказалась самой сложной и теоретически продуктивной. Мы уже отметили, что формированием структуры электрона и его поведением управляют 23 константы. Самая фундаментальная из них открыта немецким учёным Максом Планком. Она действительно фундаментальна, но он ошибся, назвав её новым научным понятием «Квант наименьшего действия», которое, как ему показалось, отражает новый физический смысл нового физического процесса.

Проверив правильность этого действия, мы сразу установили, что из размерности «Кванта наименьшего действия» следует правильный физический смысл константы Планка - «Кинетический момент» (52).

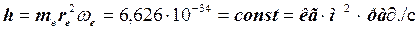. (52)

«Константа Планка» (52) с реальным давно существующим физическим смыслом кинетического момента позволяет определить угловую скорость 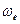вращения тора электрона относительно его центральной оси (рис. 39, b).

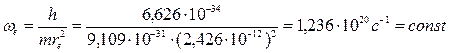(53)

Скорость 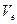точек вращающегося базового кольца (рис. 39, а) электрона равна скорости света .

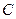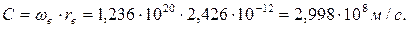(54)

Угловую скорость 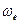(53) вращения кольца электрона мы определили, используя Константу Планка (52). Поскольку электрон проявляет одновременно электрические и магнитные свойства и имеет кинетический момент 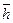, то у нас есть основания предполагать, что электрон имеет два вращения. Обычное вращение относительно оси симметрии с угловой частотой 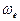назовем кинетическим вращением, формирующим его кинетический момент 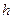и кинетическую энергию 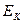. И второе - вихревое вращение относительно кольцевой оси тора с угловой частотой 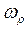(рис. 39, b). При этом

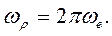(55)