Основные свойства жидкостей

Глава 2

Основы гидромеханики

Основные свойства жидкостей

Гидромеханикой называется наука о равновесии и движении жидкости и о взаимодействии жидкости с твердыми телами.

Гидромеханика, представляя собой, раздел общей механики, подразделяется на гидростатику и гидродинамику.

В гидростатике изучаются жидкости в состоянии покоя, в гидродинамике - в состоянии движения.

В гидродинамике рассматриваются тела, характеризующиеся легкой подвижностью (текучестью). Тела, обладающие текучестью, способны, не дробясь на части, изменять свою форму при действии незначительных усилий. Такие тела называются жидкостями.

Под жидкостью в гидромеханике понимают жидкие и газообразные среды, так как им присущи общие свойства, а наблюдающиеся явления можно описать одинаковыми зависимостями. Однако между капельными жидкостями и газами имеются отличия:

Основными механическими свойствами жидкости являются:

Весомость жидкости характеризующейся удельным весом - отношением веса жидкости р к занимаемому объему v

γ = р/v.

Плотность жидкости - отношение массы жидкости m к ее объему v

ρ = m/v.

Плотность и удельный вес связаны между собой зависимостями γ = ρg, где g = 9,81 м/с² - ускорение свободного падения. В судовых расчетах принимают:

для пресной воды ρ = 1,0 т/м³ (102 кгс·с²/м⁴), γ = 9,81 кН/м³;

для морской воды стандартной плотности ρ = 1,025 т/м³, (105 кгс·с²/м⁴), γ = 10,06 кН/м³;

для воздуха ρ = 1,225 кг/м³ (0,125 кгс·с²/м⁴), γ = 12,02 Н/м³.

Поверхностным натяжением называется свойство жидкости испытывать дополнительное давление на свободной поверхности под действием молекулярных сил сцепления. Это свойство жидкости характеризуется коэффициентом поверхностного натяжения α.

Вязкость – способность жидкости оказывать сопротивление при скольжении одной ее части относительно другой. Сила внутреннего трения F пропорциональна изменению скорости жидкости υ в направлении, перпендикулярном движению, и зависит от площади S соприкосновения элементов жидкости

F = μ·(dυ/dy)·S.

Это закон вязкого трения Ньютона. Коэффициент пропорциональности в нем называется коэффициентом динамической вязкости - μ (Па·с).

Отношение коэффициента динамической вязкости к плотности жидкости называется коэффициентом кинематической вязкости

ν = μ/ ρ.

Коэффициент кинематической вязкости зависит от температуры. При температуре 20⁰ С для воды он составляет 1·10^-6 м²/с, для воздуха - 1,5·10^-5 м²/с.

Гидростатика

Гидростатика изучает законы равновесия жидкой среды и взаимодействие жидкости с твердыми телами, т.е. в ситуациях, когда движение отсутствует или скорость пренебрежительно мала.

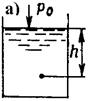
Гидростатика позволяет понять некоторые свойства такой важной гидродинамической величины, как давление. Давление твердого тела определяется его весом, давление жидкости - ее глубиной. Сила давления на дно сосуда р (рис.1,а) не зависит от его формы, а определяется только уровнем налитой в сосуд жидкости в соответствии с гидростатической формулой:

р = р₀ + ρgh;

р = р₀ + р_м ,

где ρ - плотность жидкости, р₀ - давление жидкости на некотором фиксированном уровне (при наличии свободной поверхности - атмосферное давление), h - отстояние по вертикали от этого уровня до рассматриваемой точки (глубина погружения), р_и - избыточное (манометрическое) давление.

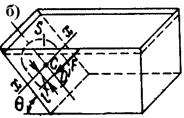
Соприкасаясь с твердым телом, жидкость оказывает на него давление, направленное по нормали к поверхности тела. Сила избыточного давления жидкости на плоскую поверхность, имеющую вертикальную ось симметрии (рис.1,б)

F = ρgh_cS,

где h_c - отстояние по вертикали ц.т. площади поверхности от уровня свободной поверхности жидкости; S - площадь поверхности.

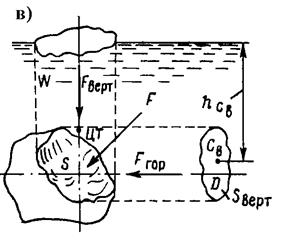Рис.1. Гидростатическое давление и сила давления жидкости.

Точка D приложения равнодействующей сил давления на поверхность называемая центром давления (ц.д.), отстоит от ц.т. площади (C) на расстоянии l.

Силу избыточного давления на криволинейную поверхность (рис.1,в) определяют ее составляющие F_x , F_y и F_z, по осям координат

F = .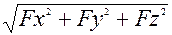

Горизонтальная составляющая силы давления на криволинейную поверхность (F_x или F_y )

F_гор = ρgh_cвS_верт,

где h_cв - отстояние по вертикали ц.т вертикальной проекции от плоскости гидростатического напора (рис. 1,в ).

Линия действия силы F_гор проходит через центр давления D площади вертикальной проекции S_верт.

Вертикальная составляющая силы давления на криволинейную поверхность, равна весу цилиндра жидкости, ограниченного снизу поверхностью, а сверху плоскостью гидростатического напора (рис.2,а) проходит через ц.т. объема

F_верт = ρgW.

Призма над криволинейной поверхностью называется телом давления.

Объем тела давления W не обязательно совпадает с действительным объемом сосуда. Если жидкость находится под криволинейной поверхностью, объем тела давления определяется объемом над поверхностью до плоскости гидростатического напора, а сила направлена вертикально вверх (рис.2,б).

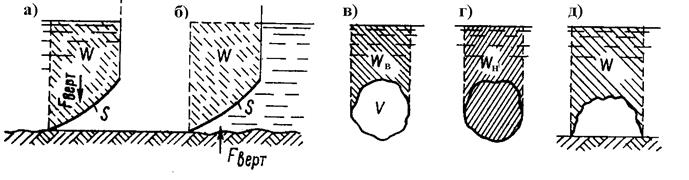
Рис.2. Силы давления на криволинейные поверхности.

Когда тело плавает на поверхности жидкости, объем тела давления равен объему вытесненной им воды V, т.е. объемному водоизмещению (рис.2 в,г)

F = ρgV.

Когда тело полностью погружено в жидкость, объем тела давления верхней половины его поверхности равен W_в, а нижней -W_н.

Вертикальную составляющую в таких случаях называют силой выталкивания (для плавающих тел - сила поддержания или плавучести)

F = ρg(W_н – W_в) = ρgV.

В результате получаем закон Архимеда: на погруженное в воду тело действует сила, равная весу вытесненной им воды, и направленная по вертикали вверх. Линия действия этой силы проходит через центр тяжести вытесненного объема V.

Закон Архимеда в обычной форме не применим к телам имеющие контактные со стенками сосуда поверхности, между которыми не может проникнуть жидкость. Такое тело испытывает со стороны жидкости только усилие ρgW, прижимающее его к грунту (рис.2,д). Но как только на контактную поверхность просочится жидкость, появится выталкивающая тело сила.

Гидродинамика

Гидродинамика изучает движение жидкости, которое может быть установившимся и не установившимся.

Движение называется установившимся, если в каждой точке неподвижного пространства, занятого движущейся жидкостью, ско-

рости не зависят от времени и, следовательно, остаются постоянными. В противном случае движение является неустановившимся.

Характер движения жидкости может быть ламинарным и турбулентным. Под ламинарным движением жидкости понимают такое движение, в котором отсутствует пульсация скоростей, приводящая к перемешиванию частиц. Если движение жидкости происходит с пульсацией скоростей, вызывающей перемешивание частиц потока, то такое движение называется турбулентным.

В гидродинамике используется понятие о линиях тока. Линии тока - линии, касающиеся вектора скорости потока. При установившемся движении жидкости линии тока и траектории движения частиц жидкости совпадают, при неустановившемся - не совпадают.

Поверхность, образуемую линиями тока, проходящими через замкнутый контур, называют трубкой тока; жидкость, заполнившая трубку тока, - элементарной струйкой.

Наглядное представление о линиях тока дает рассмотрение обтекания крыла самолета равномерным потоком воздуха. Из рис.3. видно, что снизу линии тока не очень сильно искажены, т.к. там увеличение скорости потока незначительно. Верхняя сторона крыла гораздо сильнее изменяет течение воздуха - там линии тока сжимаются и скорость заметно больше, чем в самом потоке.

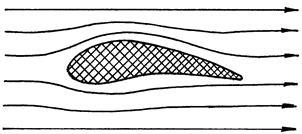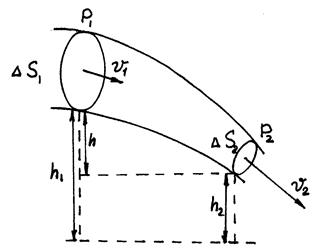Рис.3. Обтекания крыла равномерным Рис.4. К выводу уравнения

потоком воздуха. Бернулли.

Описать движение жидкости гораздо труднее, чем решить задачи гидростатики, поэтому в гидродинамике широко используют уравнения неразрывности и уравнения Бернулли.

Уравнение неразрывности выражает закон сохранения масс и используется в форме:

υ₁S₁ = υ₂S₂ = …= υ_nS_n = Q = const.

Здесь υ-скорость жидкости, S - площадь сечения трубки тока, Q - объемный расход потока. Сформулировать этот закон можно так: через любое поперечное сечение трубки тока в единицу времени протекает одинаковое количество жидкости.

Одно из важнейших уравнений гидромеханики было получено Даниилом Бернулли (рис.4.). Ему впервые удалось описать движение несжимаемой идеальной жидкости (силы трения между элементами идеальной жидкости, а также между идеальной жидкостью и стенками сосуда отсутствуют). Уравнение Бернулли имеет вид:

р + ρυ²/2 + ρgh = const,

где р - давление жидкости, ρ - ее плотность, υ - скорость движения, g - ускорение свободного падения и h - высота, на которой находится элемент жидкости. Уравнение Бернулли выражает закон сохранения энергии и условие неразрывности течения идеальной жидкости.

В этом уравнении все слагаемые имеют размерность давления и соответственно называются:

р - статическое давление;

ρυ²/2 - динамическое давление;

ρgh - весовое давление.

Можно отметить, что при отсутствии скорости уравнение Бернулли превращается в гидростатическую формулу. Изменение скорости, согласно второму закону Ньютона, происходит под действием силы, которая действует на жидкость, - в данном случае это либо сила тяжести, либо разность давлений, действующих на объем текущей жидкости.

В уравнении Бернулли два слагаемых:

ρυ²/2 - кинетическая энергия единицы объема движущейся жидкости и ρgh - потенциальная энергия единицы объема жидкости,

точно такие, как в уравнении сохранения энергии для материальной точки. Специфика гидромеханики проявляется в присутствии давления р - перепад давлений в разных частях трубки тока заставляет жидкость двигаться с ускорением, и именно поэтому в формуле Бернулли помимо кинетической и потенциальной энергий единицы объема жидкости присутствует еще и давление.

Следовательно, если труба (или трубка тока) устроена так, что давление в ней остается постоянным, уравнение Бернулли для жидкости просто совпадает с законом сохранения энергии для материальной точки. Если же труба устроена так, что можно не учитывать изменение высоты h (в силу малой плотности вещества или малого изменения этой высоты), то в соответствии с уравнением неразрывности скорость в узких участках трубы растет, - значит, там должно падать давление. Это естественный результат, поскольку рост скорости (ускорения) может быть обеспечен только за счет перепада давления и в том месте, где скорость большая, давление должно быть мало.

Уравнение Бернулли просто объясняет множество явлений рассматриваемых в курсе “теория судна”. Например, крыло, которое обтекает равномерный поток воды даже при отсутствии угла атаки, имеет подъемную силу. На суда идущими параллельным курсом слишком близко один к другому, действует гидродинамическая сила, толкающая их друг к другу. Большие скорости потока жидкости, создающиеся при быстром вращении судового винта, приводят к появлению кавитации, способной разрушить его лопасти. Принцип работы судового лага, основан также на уравнении Бернулли, позволяющий измерить скорость движения жидкости.