Работа силы. Энергия. Закон сохранения энергии

1. Работа силы. Работой силы 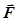на перемещении 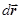называется скалярное произведение 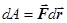. (18.1)

Так как 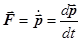, то получаем 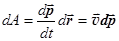. (18.2)

Это ещё одно выражение для работы через скорость и импульс.

Работа на конечном отрезке траектории L определяется криволинейным интегралом вдоль траектории. A = 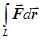. (18.3)

Единица работы в СИ – джоуль; 1 Дж = 1 Н×м.

2. Мощность. Отношение работы к времени, в течение которого она была совершена, называется мощностью. P = 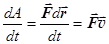. (18.4)

Единица мощности в СИ – ватт; 1 Вт = 1 Дж/с. Она названа так в честь Джеймса Уатта (I736 –I8I9) – шотландского изобретателя, создателя универсального парового двигателя (I784). Ввел первую единицу мощности – лошадиную силу, 1 л.с. = 735 Вт.

3. Консервативные силы. Силы, работа которых не зависит от формы траектории, а определяется лишь начальным и конечным положением тела, называются консервативными.

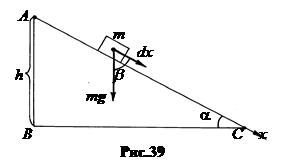Примером консервативной силы является сила тяжести. Вычислим работу, совершаемую силой тяжести при скатывании тела по наклонной плоскости. (AB = h, AC = L). (рис.39)

dA= 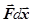=mgcosb×dx=mgsina×dx.

A= 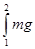sina×dx = mgsina 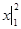, Þ A = mgsina (x₂ – x₁).

Но x₂ – x₁ = L – длина наклонной плоскости, Lsina = h – высота начальной точки движения 1 над конечной точкой движения 2. Итак, A = mgh. (18.5)

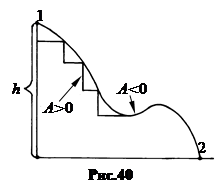
В общем случае тело может двигаться по любой другой траектории, и во всех случаях работа силы тяжести A = mgh (рис.40).

В этом можно убедиться, если разбить всю криволинейную траекторию на малые участки так, чтобы на каждом отрезке траектории можно было пренебречь кривизной и полагать его участком наклонной плоскости. Там, где траектория идет вниз, работа положительна, а где траектория идет вверх – отрицательна. А суммарная работа так же определится разностью высот точек 1 и 2.

Итак, сила тяжести – это консервативная сила.

А сила трения, например, неконсервативная. Работа силы трения зависит от формы пути движения и всегда отрицательна, так как сила трения всегда противоположна скорости. Силу трения называют ещё диссипативной силой. (От латинского dissipatio – рассеяние).

Кроме силы тяжести консервативными являются все центральные силы, которые направлены вдоль прямой, проходящей через взаимодействующие материальные точки. Это, например, силы гравитации, кулоновские силы, силы упругости.

Если тело перемещать по замкнутому пути, то работа консервативных сил равна нулю. Например, в случае движения по наклонной плоскости работа вниз A_1®2 = mgh, а работа вверх A_2®1 = –mgh. Суммарная работа равна нулю.

Системы, в которых действуют только консервативные силы, называются консервативными.

4. Потенциальная энергия.Понятие потенциальной энергии для консервативной системы вводится так. Какое-либо произвольное состояние системы с известными координатами материальных точек принимается за нулевое. Работа, совершаемая консервативными силами при переходе системы из любого положения в нулевое, называется потенциальной энергией системы в данном положении.

Например, полагаем состояние системы Земля – карандаш нулевым, когда карандаш лежит на полу комнаты. Если карандаш поднять на высоту h над полом, то потенциальная энергия системы Земля – карандаш составляет mgh, поскольку именно такую работу совершает сила тяжести независимо от формы траектории, перемещая карандаш с высоты h на пол комнаты. Здесь m – масса карандаша.

Потенциальная энергия системы – будем обозначать её символами E_п или U – является функцией только координат её материальных точек. Иначе, потенциальная энергия – функция состояния системы. Работа, которую совершает система, переходя из одного состояния в другое, равна убыли её потенциальной энергии, dA = –dE_п . (18.6)

5. Кинетическая энергия. Когда тело движется по наклонной плоскости (без трения) или карандаш свободно падает, их скорости непрерывно увеличиваются. По-видимому, это происходит благодаря работе силы тяжести.

Вычислим работу консервативной силы, изменяющей скорость движения тела от v₁ до v₂. По формуле 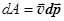в случае малых скоростей, когда v << c, 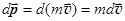. Если скорость изменяется только по величине, то векторы vи dv сонаправлены, и 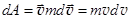. Отсюда A = 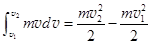. (18.7)

Величину 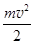= E_к называют кинетической энергией материальной точки.

Итак, работа силы, изменяющей величину скорости движения материальной точки от v₁до v₂,равна приращению кинетической энергии точки: A = E_К2 – E_К1. (18.8)

Кинетическая энергия СМТ равна сумме кинетических энергий всех материальных точек, из которых эта система состоит. Как и масса, кинетическая энергия – всегда положительное число.

6. Энергия и преобразования Галилея. Потенциальная энергия СМТ является функцией отрезков. Например, потенциальная энергия системы Земля – карандаш определяется расстоянием, в общем случае, между центрами их масс. Это расстояние не зависит от того, в какой системе отсчета оно измеряется. Говорят, отрезки инвариантны преобразованиям Галилея. А это значит, что и значение потенциальной энергии СМТ также не зависит от выбора системы отсчета. Итак, потенциальная энергия СМТ инвариантна преобразованиям Галилея.

Иначе обстоит дело с кинетической энергией СМТ. Поскольку кинетическая энергия тела определяется скоростью движения тела, то важно, относительно какого тела отсчета эта скорость измеряется. При переходе из одной системы отсчета в другую скорость материальной точки меняется (скорость не инвариантна преобразованиям Галилея). Например, скорости движения двух автомобилей, идущих по дороге в одну сторону, относительно стоящего на обочине пешехода составляют 100 км/час одного и 90 км/час другого. А относительно пассажиров, находящихся в этих автомобилях, скорость соседней машины составляет всего лишь ±10 км/час. Поскольку кинетическая энергия пропорциональна квадрату скорости, то ясно, сколь существенно будут отличаться энергии движения автомобилей относительно друг друга и относительно стоящего пешехода.

Итак, кинетическая энергия СМТ не инвариантна преобразованиям Галилея. Её значение зависит от выбора системы отсчета.

7. Сохранение энергии в консервативных системах. Если работа в системе совершается за счет потенциальной энергии системы, а в системе действуют только консервативные силы (нет сил трения), то результат работы – изменение кинетической энергии системы. A_1®2 = E_П1 – E_П2 = E_К2 – E_К1, или E_П1 + E_К1 = E_П2 + E_К2 = const. (18.9)

Следовательно, в консервативной системе полная механическая энергия системы E_П + E_К = const остаётся постоянной. В системе могут происходить лишь превращения потенциальной энергии в кинетическую или обратно, но полный запас механической энергии системы измениться не может.

В этом суть закона сохранения энергии в консервативных системах.

8. Сохранение энергии в неконсервативных системах. Если в системе действуют силы трения, то кинетическая энергия такой системы постоянно уменьшается по сравнению с консервативной, а вместе с ней уменьшается и полная механическая энергия системы. С точки зрения формальной макроскопической механики энергия системы бесследно исчезает. Закон сохранения механической энергии не выполняется.

Но если рассматривать систему на общефизическом уровне с учётом её микроскопической структуры, то выясняется, что при ударе и трении кинетическая энергия видимого движения не пропадает; она лишь переходит в кинетическую энергию невидимого беспорядочного движения атомов и молекул вещества. Эта форма энергии тела называется внутренней энергией, её увеличение макроскопически проявляется в повышении температуры тела.

Таким образом, с учетом немеханических форм энергии общефизический закон сохранения энергии формулируется так:

Энергия не создаётся и не уничтожается, она может лишь переходить из одной формы в другую.

Общефизический закон сохранения и превращения энергии охватывает все физические явления, в том числе и те, к которым модели механики не применимы. Следовательно, этот закон не может быть выведен из уравнений макроскопической механики, а должен рассматриваться как самостоятельный опытный закон природы, основывающийся на громадном количестве фактов.