Электрические фильтры

Вопросы:

1. Классификация фильтров.

2. Частотные характеристики основных типов фильтров.

3. Элементы синтеза фильтров.

Радиотехнический фильтр – это устройство, обладающее частотной избирательностью и предназначенное для селекции электрических колебаний в заданной полосе частот.

Область частот, в которой фильтр пропускает колебания с небольшим затуханием, называется полосой пропускания фильтра (полосой прозрачности фильтра).

Фильтры классифицируются по различным признакам:

- по типам схем

- по используемым элементам

- по пропускаемым частотам

Фильтры бывают

Классификация по типам схем:

-Г-образные РИСУНОК

-П-образные РИСУНОК

-Т-образные РИСУНОК

-Лестничные РИСУНОК

- Мостовые РИСУНОК

Классификация по применяемым элементам:

- Реактивные ( -фильтры)

- Безындукционные ( 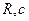-фильтры)

- Электромеханические фильтры

Классификация по пропускаемым частотам:

- фильтры низких частот (ФНЧ)

- фильтры верхних частот (ФВЧ)

- полосовые фильтры (ПФ)

- режекторные (заградительные) фильтры (РФ)

Частотные характеристики основных типов фильтров

ФНЧ

Фильтры нижних частот пропускают колебания с частотами ниже заданной, которая называется частотой среза и подавляет колебания других, более высоких частот.

Следовательно, АЧХ ФНЧ имеет вид:

РИСУНОК

Частота среза – это такая частота, на которой модуль коэффициента передачи в 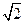раз меньше максимального значения.

Полоса пропускания – это область частот, в пределах которой модуль коэффициента передачи больше либо равен .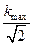

Важнейшая характеристика фильтра – коэффициент прямоугольности .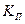

Для ФНЧ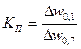

РИСУНОК

Коэффициент прямоугольности идеального фильтра равен 1.

Таким образом, коэффициент прямоугольности показывает, насколько АЧХ близка к идеалу. У реальных фильтров коэффициент прямоугольности всегда больше 1.

Для сравнения нескольких фильтров, бывает удобно пронормировать АЧХ.

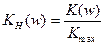
Нормированная АЧХ ФНЧ будет иметь вид:

РИСУНОК

Схемы простейших фильтров нижних частот:

- Безындукционный фильтр ( 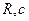-фильтр)

РИСУНОК

- Реактивный фильтр ( -фильтр)

РИСУНОК

Получим выражение для АЧХ фильтра нижних частот

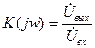
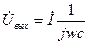
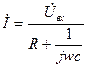
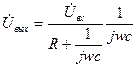
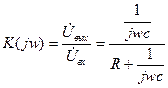
РИСУНОК

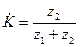
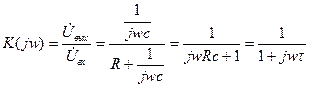
где 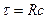- постоянная времени цепи

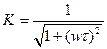
РИСУНОК

РИСУНОК

ВФЧ

Фильтр верхних частот – пропускает колебания с частотами больше заданной и подавляют колебания более низких частот.

РИСУНОК

Нормированная АЧХ ФВЧ имеет вид:

РИСУНОК

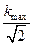- модуль пропускания частоты среза

Для ФВЧ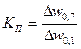

Схемы ФВЧ:

- Безындукционная ( 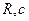-фильтр по сравнению с ФНЧ 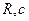меняются местами)

- Реактивная ( -фильтр по сравнению с ФНЧ меняются местами)

Полосовой фильтр

Полосовые фильтры пропускают колебания в заданной полосе частот от до 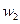и подавляют колебания за пределами данной полосы.

Т.е. нормированная АЧХ ПФ:

РИСУНОК

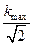дает и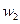

Для ПФ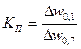

Схемы ПФ:

РИСУНОК

Режекторный фильтр

Режекторный или заградительный фильтр – не пропускает колебания в полосе частот до 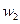и пропускает колебания за пределами этой полосы.

Т.е. нормированная АЧХ РФ:

РИСУНОК

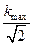дает и

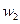
- полоса режекции

Для ПФ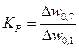

Схемы РФ:

РИСУНОК

(Обратная ПФ)

Элементы синтеза фильтров

Задача синтеза фильтров заключается в отыскании схемы и элементов фильтра по заданной АЧХ. Для решения этой задачи существуют несколько методов. Один из них называется:

Метод максимально гладкой аппроксимации. В этом методе выражение для АЧХ ФНЧ представляется следующим соотношением

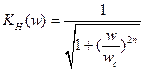
n – количество реактивных элементов в схеме фильтра

По этой формуле АЧХ аппроксимируется примерно следующим образом:

РИСУНОК

По этой формуле можно рассчитать количество реактивных элементов в зависимости от требуемого коэффициента прямоугольности. Для этого найдем значения нормированного коэффициента передачи на частоте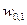

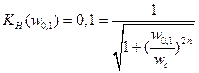
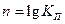
Последовательный колебательный контур

Вопросы:

1. Схемы и параметры последовательного колебательного контура

2. Резонанс напряжений

3. Частотные характеристики последовательного колебательного контура.

Последовательный колебательный контур (ПСКК) – это цепь, в которой элементы 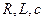соединены последовательно с источником ЭДС.

РИСУНОК

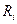- внутреннее сопротивление источника.

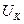- напряжение на входе контура

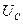- напряжение на выходе контура

Сопротивление потерь

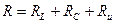
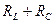- потери в емкости и индуктивности

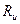- потери на излучение

Активное сопротивление R не зависит от частоты.

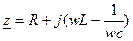
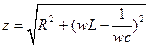
Графики зависимости всех сопротивлений от частоты:

РИСУНОК

Параметры 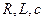- первичные параметры.

Существует некоторая частота, на которой

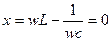
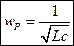- резонансная частота

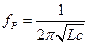
На резонансной частоте сопротивление контура чисто активно

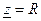
На частотах меньше резонансной, сопротивление контура носит активно емкостной характер.

На частотах больше резонансной, сопротивление контура носит активно индуктивный характер.

Настроить контур в резонанс можно двумя способами:

Первый способ – изменять индуктивность и емкость при неизменной частоте входного сигнала. Этот способ используется при эксплуатации радиоаппаратуры.

Второй способ – изменением частоты генератора при фиксированных . Этот способ применяется в лабораторных условиях при ремонте и наладке аппаратуры.

Резонанс напряжений

Рассмотрим свойства контура на резонансной частоте.

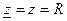
Сопротивление контура чисто активно, модуль сопротивления принимает минимальное значение.

Величина тока в контуре

- самый большой по сравнению с током на других частотах.

Сдвиг фаз между напряжением и током на резонансной частоте

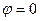
Сопротивление каждого из реактивных элементов контура на резонансной частоте называется характеристическим сопротивлением, обозначается буквой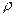

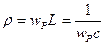
Если выразить характеристическое сопротивление через индуктивность и емкость

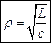
На резонансной частоте падение напряжений на реактивных элементах максимально

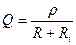
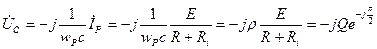
Напряжения на индуктивности и емкости равны по величине и в 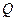раз превышают ЭДС источника.

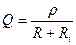- добротность

В радиотехнических устройствах добротность составляет от десятков до сотен единиц.

Это явление называется резонансом напряжений.

Резонанс напряжений – это явление, при котором напряжения на реактивных элементах контура равны по величине и в 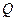раз превышают ЭДС источника.

Напряжение на индуктивности на 90 градусов впереди тока, а напряжение на емкости на 90 градусов позади тока. Таким образом, друг относительно друга эти напряжения в противофазе.

РИСУНОК

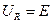
В колебательном контуре происходит обмен энергией между емкостью и индуктивность. Так же имеют место потери энергии на активном сопротивлении (нагрев элементов).

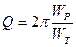
- энергия, запасенная в контуре

- энергия тепловых потерь

Т.е. добротность характеризует свойство контура запасать энергию.

Величина, обратная добротности называется затуханием

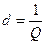
Величины 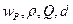называются вторичными параметрами контура.

Резонансные свойства последовательного колебательного контура

Резонансная кривая – это зависимость тока от частоты питающей ЭДС.

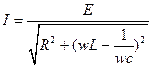
РИСУНОК

Из графика можно сделать вывод, что последовательный колебательный контур обладает частотной избирательностью.

Резонансная кривая несимметрична, но обычно интересуются областью вблизи резонансной частоты – область малых растроек (ОМР).

Различают следующие виды растроек:

- абсолютная растройка 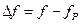или 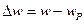, т.е. разность между частотой источника и резонансной частотой.

- относительная растройка 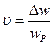т.е. отношение абсолютной растройки к резонансной частоте.

-обобщенная растройка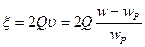

Получим выражение реактивной составляющей сопротивления контура в области малых растроек.

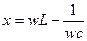- в это выражение подставим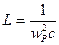

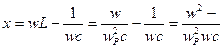
Занятие 2.4.2. Последовательный колебательный контур. Продолжение.

Вопросы:

1. Комплексная частотная характеристика, АЧХ, ФЧХ.

2. Влияние сопротивлений источника и нагрузки на характеристики контура.

В качестве входного сигнала используем ЭДС источника 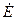. В качестве выходного чаще всего используется напряжение на емкости.

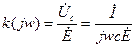
Для области малых растроек полагаем

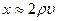
Тогда

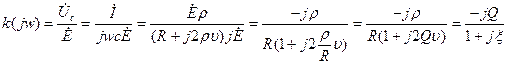
АЧХ:

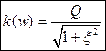
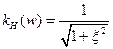
ФЧХ:

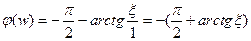
РИСУНОК – ненормированная АЧХ

РИСУНОК– нормированная АЧХ

Полоса пропускания и избирательность

Для отыскания полосы пропускания, воспользуемся выражением для нормированного АЧХ.

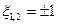
На границах полосы пропускания, обобщенная растройка равна 1 и -1.

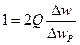
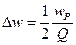
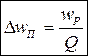
Для отыскания коэффициента прямоугольности

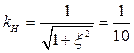
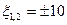
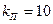
Влияние сопротивление нагрузки и источника на резонансные характеристики контура. Влияние сопротивления источника.

Сопротивление источника включено последовательно с контуром, поэтому эквивалентная добротность (добротность контура вместе с источникам)

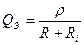
Таким образом, с увеличением сопротивления источника добротность уменьшается и полоса пропускания растет.

Влияние нагрузки

РИСУНОК

Преобразуем РИСУНОК в РИСУНОК.

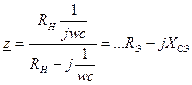
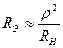
Эквивалентная добротность с источником и нагрузкой

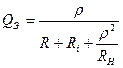
С увеличением нагрузки добротность возрастает, а полоса пропускания уменьшается.

Параллельный колебательный контур. Продолжение.

Вопросы:

1. Резонансные кривые, АЧХ, ФЧХ.

2. Влияние сопротивлений источника и нагрузки на характеристики контура.

3. Сложные параллельные колебательные контуры.

Резонансные кривые ПРКК – это зависимость тока в общей ветви или напряжения на контуре от частоты питающей ЭДС.

Для анализа характеристик рассмотри следующую схему:

РИСУНОК

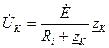
1.

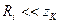
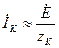
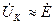
РИСУНОК

Напряжение на контуре примерно равно напряжению источника и от частоты не зависит. Ток в контуре обратно пропорционален модулю его сопротивления.

2.

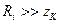
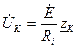
РИСУНОК

Ток от частоты не зависит, а напряжение на контуре прямо пропорционально модулю его сопротивления.

3. Наиболее часто на практике применяется случай

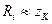
Это необходимо для того, чтобы из источника в контур передавалась максимальная мощность.

В этом случае применяются исходные формулы и резонансные кривые выглядят следующим образом:

РИСУНОК

Для того, чтобы параллельный обладал избирательными свойствами по напряжению, необходимо чтобы сопротивление источника было больше либо равно сопротивлению контура .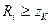

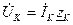
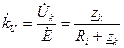
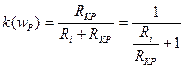
Коэффициент передачи по напряжению даже на резонансной частоте все равно меньше единицы. Он был бы равен 1, если бы сопротивление источника было нулевым.

Параллельный колебательный контур усилительными свойствами по напряжению не обладает.

АЧХ, ФЧХ

Поскольку контур – это часть схемы, с которой снимается напряжение, то

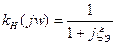
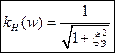
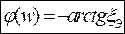
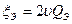
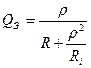
Ненормированная АЧХ будет выглядеть так:

РИСУНОК

Полоса пропускания параллельного контура – это область частот, в пределах которой сигнал проходит с ослаблением не большим, чем 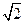раз по сравнению с ослаблением на резонансе.

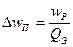
Влияние сопротивления источника и нагрузки

на характеристики контура

Проанализировав формулы эквивалентной добротности, следует, что с ростом сопротивления источника добротность возрастает, а полоса пропускания уменьшается. При этом следует помнить, что уменьшается так же и коэффициент передачи по напряжению.

Для оценки влияния нагрузки проанализируем такую схему:

РИСУНОК

Формула эквивалентной добротности параллельного контура, учитывающая и источник и нагрузку имеет следующий вид:

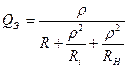
Т.е. с увеличением 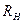добротность возрастает, полоса пропускания уменьшается.

Сложные ПРКК

Для того, чтобы в контур поступала максимальная мощность, надо выполнить условие

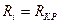
Или чтобы из контура в следующий каскад уходил максимальная мощность, надо обеспечить условие

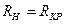
Т.е. надо согласовать сопротивления. Это не всегда возможно и бывает что нагрузка меняется. Помочь разрешить данную задачу могут сложные ПРКК.

Обобщенная схема сложных ПРКК такая:

РИСУНОК

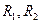- активные сопротивления ветвей

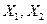- реактивные сопротивления ветвей

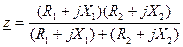
Вблизи резонансной частоты

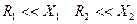
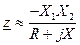
Сопротивление контура при резонансной частоте

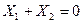
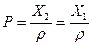- коэффициент включения

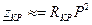
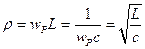
где - общая индуктивность и емкость, получаемая при последовательном обходе всего контура.

Контур второго рода:

РИСУНОК

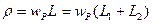
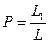
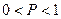
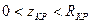
Одна из ветвей контура второго рода представляет собой последовательный контур 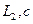, т.е. в этом контуре возникает резонанс напряжений.

На частоте 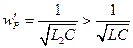, которая больше основной резонансной частоты

АЧХ

РИСУНОК

Это свойство называется фильтрацией и иногда используется для подавления помехи.

Контур третьего рода:

РИСУНОК

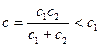
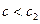
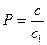
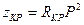
АЧХ

РИСУНОК