Частотно-избирательное свойство линейных цепей. Электрические фильтры
Занятие 2.3.1. Общие сведения частотно-избирательных цепях
Вопросы:
1. Общие сведения о частотно-избирательных цепях.
2. Частотные характеристики линейных цепей.
В радиотехнике имеют дело со сложными сигналами, в составе которых много гармоник. Используются сигналы с ограниченным спектром, т.е. 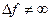 . Это позволяет в заданной полосе частот разместить несколько радиотехнических средств.
. Это позволяет в заданной полосе частот разместить несколько радиотехнических средств.
РИСУНОК
Таким образом, возникает задача частотной селекции.
Частотная избирательность (селективность) – это свойство линейной цепи выделять сигнал определённой частоты из всей совокупности сигналов, поступающих на её вход. Практически, частотная избирательность реализуется с помощью различного рода фильтров.
Пусть на вход линейной цепи поступает гармонический сигнал 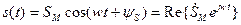
РИСУНОК!!!
Выходной сигнал линейной цепи тоже будет гармоническим
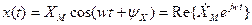
С такой же частотой, что и на входе, но в общем случае с другой амплитудой и начальной фазой.
Комплексный коэффициент передачи – отношение комплексной амплитуды выходного сигнала к комплексной амплитуде входного сигнала
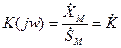
Если входной сигнал – это ток, а выходной сигнал – напряжение, то
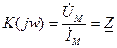 Ом – передаточное сопротивление
Ом – передаточное сопротивление
Если входной сигнал – это напряжение, а выходной сигнал – ток, то
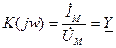 См – передаточная проводимость
См – передаточная проводимость
Если входной сигнал – это напряжение, и выходной сигнал – напряжение, то
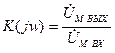 - коэффициент передачи по напряжению
- коэффициент передачи по напряжению
Если входной сигнал – это ток, и выходной сигнал – ток, то
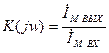 - коэффициент передачи по току
- коэффициент передачи по току
Существует несколько способов нахождения комплексного коэффициента передачи:
Задали произвольное входную амплитуду 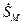 . Зная схему цепи, применив любой из методов расчета, найти выходную амплитуду
. Зная схему цепи, применив любой из методов расчета, найти выходную амплитуду 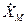 . Поделить.
. Поделить.
Комплексный коэффициент передачи можно получить, пользуясь любой системой параметров четырехполюсника.
Если четырехполюсники соединены каскадно, и каждый имеет свой собственный комплексный коэффициент передачи, то общий коэффициент будет
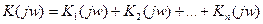
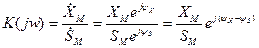
Из данного уравнения следует экспериментальный способ определения комплексного коэффициента передачи:
На вход линейной цепи подается гармоническое напряжение известной амплитуды. Измеряется амплитуда выходной гармоники и фазовый сдвиг между входной и выходной гармоникой. Вычисляется комплексный коэффициент передачи
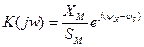
Если в цепи есть хоть один реактивный элемент, то комплексный коэффициент передачи разный для разных частот.
Амплитудно-частотная характеристика (АЧХ) – зависимость модуля комплексного коэффициента передача от частоты. Графически строится в прямоугольной системе координат, где по оси абсцисс – частота, а по оси ординат – коэффициент передачи. Т.е. физически АЧХ показывает, как изменяется амплитуда выходного гармонического напряжения от частоты при неизменной амплитуде на входе.
Фазо-частотная характеристика (ФЧХ) – зависимость аргумента комплексного коэффициента передачи от частоты. Физически ФЧХ показывает, как изменяется фазовый сдвиг между выходным и входным гармоническим сигналом при изменении частоты.
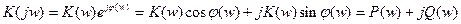
РИСУНОК
Для фиксированной частоты необходимо рассчитать модуль и аргумент (или вещественную и мнимую часть) 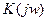 и поставить точку на комплексной плоскости. При изменении частоты
и поставить точку на комплексной плоскости. При изменении частоты 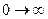 эта точка прочертит на комплексной плоскости кривую, которая называется амплитудно-фазовая характеристика (АФХ) или годограф. На АФХ в явном виде частота не указывается, но видно, в каких пределах изменяется модуль и аргумент комплексного коэффициента передачи при изменении частоты во всем возможном диапазоне.
эта точка прочертит на комплексной плоскости кривую, которая называется амплитудно-фазовая характеристика (АФХ) или годограф. На АФХ в явном виде частота не указывается, но видно, в каких пределах изменяется модуль и аргумент комплексного коэффициента передачи при изменении частоты во всем возможном диапазоне.
Логарифмические характеристики
Иногда диапазон изменения 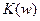 очень велик и построить АЧХ трудно. В этом случае применяют логарифмический масштаб
очень велик и построить АЧХ трудно. В этом случае применяют логарифмический масштаб
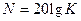 дБ - если речь идет о токе или напряжении
дБ - если речь идет о токе или напряжении
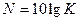 дБ - если коэффициент передачи вычисляется по мощности
дБ - если коэффициент передачи вычисляется по мощности
РИСУНОК
Если частота изменяется в очень широком диапазоне, то можно прологарифмировать и шкалу частот
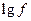 , Б
, Б
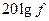 , дБ
, дБ
Дата добавления: 2018-11-26; просмотров: 1247;











