Пассивные фильтры нижних частот первого порядка

Рис.9.1. Пассивный ФНЧ первого порядка

На рис.9.1. изображена схема простого RС-фильтра нижних частот первого порядка. Коэффициент передачи в комплексном виде может быть выражен формулой:

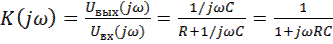. (9.7)

Отсюда получим формулы для АЧХ и ФЧХ:

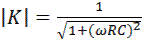. (9.8)

Положив 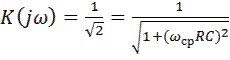, получим выражение для частоты среза ω_ср :

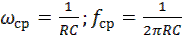. (9.9)

| К | = 1 = 0 дБ на нижних частотах f << f_ср.

На высоких частотах f >>f_ср согласно формуле (9.8) |К| ≈ 1/ (ωRC), т.е. коэффициент передачи обратно пропорционален частоте. При увеличении частоты в 10 раз коэффициент усиления уменьшается в 10 раз, т. е. он уменьшается на 20 дБ на декаду или на 6 дБ на октаву. 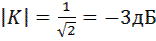при f = f_ср.

Пример расчета пассивного ФНЧ первого порядка.

Произведем расчет коэффициента передачи по формуле 9.8. Для этого примем, что R = 1 кОм и С = 1 мкФ. Будем принимать частоту от 0,001 Гц до 100 кГц с шагом 10. Получаем следующие расчеты коэффициента передачи фильтра:

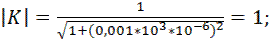
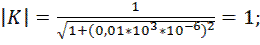
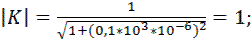
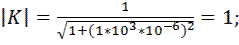
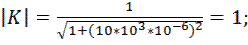
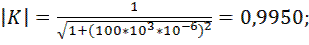
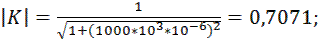
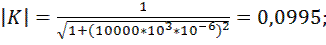
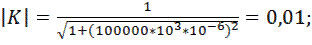
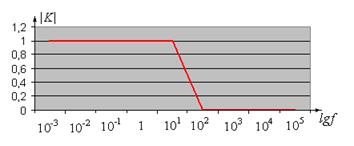
Рис.9.2. Зависимость коэффициента передачи фильтра ФНЧ от частоты

Построим график зависимости коэффициента передачи от частоты (рис.9.2).

Таким образом, видим, что ФНЧ обеспечивает нормальное прохождение низких частот и задерживает верхние частоты.

Для более быстрого уменьшения коэффициента передачи можно включить n фильтров нижних частот последовательно. При последовательном соединении нескольких фильтров нижних частот частота среза приближенно определяется как

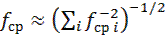. (9.10)

Для случая n фильтров с равными частотами среза

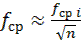. (9.11)

При частоте входного сигнала f_вх>> f_ср для схемы (рис.9.1) получим

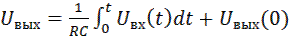. (9.12)

Из (9.12) видно, что ФНЧ может выступать как интегрирующее звено.

Для переменного напряжения, содержащего постоянную составляющую, выходное напряжение можно представить в виде

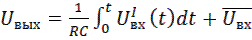, (9.13)

где 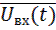- среднее значение.

Фильтр нижних частот может выступать в качестве детектора средних значений.

Для реализации общего подхода к описанию фильтров необходимо нормировать комплексную переменную р:

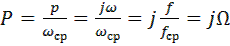. (9.14)

Для фильтра рис.9.1 получим Р = рRC и

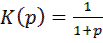. (9.15)

Используя передаточную функцию для оценки амплитуды выходного сигнала от частоты, получим

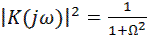. (9.16)

Передаточная функция ФНЧ в общем виде может быть записана в виде 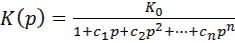, (9.17)

где с₁, с₂ ,…, с_n– положительные действительные коэффициенты.

Порядок фильтра определяется максимальной степенью переменной Р. Для реализации фильтра необходимо разложить полином знаменателя на множители. Если среди корней полинома есть комплексные, в этом случае следует записать полином в виде произведения сомножителей второго порядка

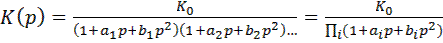, (9.18)