Поле наклонного преобразователя

В наклонном преобразователе упругие волны сначала распространяются в материале призмы, затем преломляются на границе «призма–изделие», трансформируются в поперечные и попадают в объект контроля.

Проанализируем поле наклонного преобразователя в объекте контроля в дальней зоне. Это поле создается лучами, возникшими в призме и преломленными на границе. Акустической осью преобразователя в изделии ON назовем преломленную ось АО излучения в призме (рис. 2.24). Точка О – это точка ввода. Акустическая ось ON не совпадает с центральным лучом преломленного пучка, который начинается в точке О и соответствует максимуму диаграммы направленности. Угол преломления центрального луча называют углом ввода. Существуют две основные причины отличия угла ввода от угла преломления (или отличия центрального луча от акустической оси). Первая доминирует в ОК небольшой толщины и вызвана зависимостью коэффициента прозрачности D от угла падения. Эта зависимость – уменьшение D с ростом угла 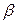– почти во всем интервале: 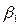< < 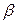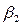приводит к смещению центрального луча в сторону меньших углов от преломленной акустической оси. В ОК значительной толщины к этому эффекту добавляется еще эффект квазиискривления акустической оси: лучи пучка, преломленные под меньшими углами, проходят и меньший путь в изделии. Следовательно, они меньше затухают; результатом будет дополнительное уменьшение угла ввода по сравнению с углом преломления.

Рис. 2.24. Схема расчета поля наклонного ПЭП

Угол преломления возрастает тем быстрее, чем больше угол падения. Поэтому диаграмма направленности наклонного ПЭП в плоскости падения становится несимметричной. Ширина основного лепестка диаграммы направленности в этой плоскости увеличена по сравнению с прямым ПЭП. Это явление выражено тем сильнее, чем больше угол призмы. Ширина раскрытия поля наклонного ПЭП в плоскости падения определяется по формуле:

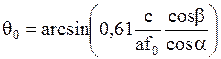. (2.34)

В плоскости, перпендикулярной плоскости падения, ширина раскрытия диаграммы направленности не зависит от угла призмы, и практически совпадает с шириной раскрытия у прямого ПЭП.

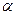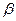Для расчета поля наклонного ПЭП вводят понятие «мнимая пьезопластина». Точка O₁ (рис. 2.24) – это точка, где сходятся продолжающая лучи пучка. Поле представляется как поле мнимого источника, помещенного в точку О₁ и имеющего эллиптическую форму с полуосями 2acos /cos в плоскости падения и 2а – в перпендикулярной плоскости. Размер ближней зоны х_б может быть вычислен по формуле:

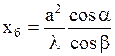. (2.35)

Акустический тракт

Акустическим трактом называют путь ультразвукового сигнала от излучателя до отражателя и далее до приемника ультразвука. Расчет акустического тракта – это определение амплитуды сигнала от отражателя в зависимости от формы и размеров отражателя и ПЭП и расстояния между ними, акустических свойств материала ОК, частоты ультразвуковой волны. Обычно акустический тракт рассчитывается для модельных отражателей, имеющих простую форму. С ростом размера дефекта амплитуда эхо-сигнала возрастает, но до определенного предела. Как правило, амплитуда сигнала от дефекта убывает с увеличением глубины его залегания. Эта зависимость вызвана двумя обстоятельствами: расхождением пучка в дальней зоне и затуханием ультразвука. По этим же причинам происходит ослабление донного сигнала, только он ослабляется медленнее, чем сигналы от большинства отражателей. Столь же медленно уменьшается амплитуда сквозного сигнала при контроле теневым методом. Чем больше размер затеняющего дефекта, тем сильнее ослабляется амплитуда.

Рассмотрим влияние формы, ориентации и заполнения отражателей на амплитуду отраженного сигнала. При равных глубине залегания и площади отражателя наибольший отраженный сигнал получается от дискового отражателя, ориентированного по нормали к оси пучка (рис. 2.25, а). Такой отражатель можно приготовить, например, выполнив плоскодонное сверление нужного диаметра на заданную глубину. От отражателя округлой формы, сферического или цилиндрического (рис. 2.25, б) амплитуда отражения меньше.

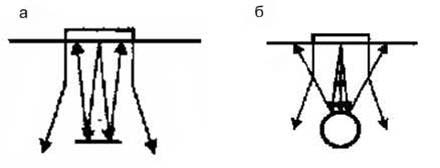
Рис. 2.25. Отражение плоскостного (а)
и округлого отражателей (б)

Амплитуда сигнала, отраженного от плоскостного отражателя, существенно зависит от ориентации пучка и плоскости отражателя. Сигнал наибольшей амплитуды получается при перпендикулярном расположении плоскости отражателя и оси пучка. Если отражатель сильно наклонен, то зеркально отраженные лучи не попадают на приемник. Отраженный сигнал создается более слабыми отражениями от кромок отражателя и полем дифракции. Указанная зависимость амплитуды сигнала от ориентации плоскостного отражателя ярко выражена для отражателей больших размеров. Если размер отражателя меньше половины длины волны, то волна огибает дефект за счет дифракции и отраженный сигнал резко уменьшается.

Коэффициент отражения ультразвука на границе дефекта, заполненного газом или воздухом, по модулю близок к единице. Для дефекта, заполненного шлаком, этот коэффициент существенно меньше. По этой причине амплитуда сигнала, отраженного от газовой поры больше, чем от шлакового включения. Слабый отраженный сигнал дают тонкие окисные плены. Вблизи границы металла с раковиной иногда располагается большое количество пор, которые рассеивают ультразвук. По этой причине может получиться слабый отраженный сигнал, даже от крупной раковины. Слабый отраженный сигнал дают и плоскостные дефекты (трещины, расслоения) с очень малым, в единицы и десятки микрон, раскрытием.

Теперь рассмотрим более подробно влияние размера отражателей и глубины их залегания. Приведем формулы для расчета акустического тракта для нескольких модельных отражателей.

В ближней зоне амплитуда отраженного сигнала сильно зависит от формы и длительности зондирующего импульса. Приближенно отношение амплитуд А/А₀ для плоского диска можно оценить по формуле:

А/А₀=(1–4) 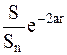, (2.36)

где S – площадь отражателя, S_n – площадь НЭП, а – коэффициент затухания, r – расстояние между ПЭП и отражателем. Множитель 2 в показателе экспоненты появился в связи с тем, что волна проходит путь – 2r до дефекта и обратно. Из-за наличия множителя (1–4) амплитуду отражения в ближней зоне можно оценить лишь очень приближенно.

Для модельных отражателей, расположенных в дальней зоне, выведены формулы для отношения амплитуд. В табл. 2.7 приведены расчетные формулы для некоторых часто встречающихся модельных отражателей в акустическом тракте прямого и наклонного преобразователя.

В табл. 2.7 S – площадь дискового или сегментного отражателя, D – коэффициент прозрачности, 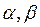– углы ввода и призмы, 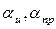– коэффициенты затухания в изделии и призме, r – расстояние в изделии от точки ввода до отражателя, 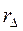– приведенное расстояние в призме, r₁ – длина акустической оси в призме.

Таблица 2.7