ФПВ и ФРВ для гармонического колебания со случайной начальной фазой.

Рассмотрим случайный процесс в виде гармонического колебания со случайной начальной фазой:

X(t) = Asin ( wt + j )

j - случайная величина, равномерно распределенная на интервале ± p, т.е. ФПВ мгновенных значений фазы , показанная на рис.11.5 равна:

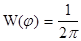; |x| £ p

W(j)

1/2p

Рис.11.5.

-p 0 p j

Вычислим среднее значение j:

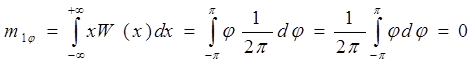
Вычислим дисперсию:

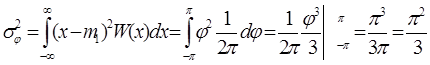
ФПВ мгновенных значений x гармонического колебания со случайной фазой, изображенная на рис. 11.6, имеет вид:

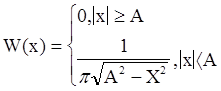
W(x)

Рис.11.6.

-A 0 A x

Чем больше А, тем кривая ниже и шире. Заштрихованная площадь равна единице. Это площадь под кривой W(x) (условие нормировки)..

ФРВ мгновенных значений для гармонического колебания со случайной фазой:

X(t) = Asin ( wt + j )

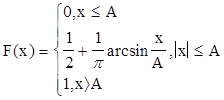
F(x)

1

0.5

Рис.11.7.

-A 0 A x

ФПВ для суммы нормального случайного процесса и гармонического колебания со случайной начальной фазой.

Рассмотрим случайный процесс z(t), равный:

Z(t) = x(t) + Asin (wt+ j)

где x(t) - нормальный случайный процесс;

Asin (wt+ j) - гармоническое колебание со случайной начальной фазой.

W(z) в этом случае находится сверткой.

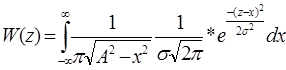
Вид ФПВ, т.е. W(z) зависит от параметра:

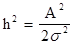
W(z)

h²=0 h²=¥

h²= 6

Рис.10.8.

0 z

h² = 0 - нормальный случайный процесс (чистый шум).

h² ® ¥ - одно гармоническое колебание.