Соотношение Винера - Хинчина и его применение к решению задач

Это соотношение связывает функцию корреляции и энергетический спектр случайного процесса. В теории случайных процессов это соотношение аналогично преобразованию Фурье для детерминированных процессов:

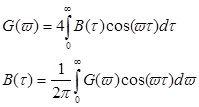(14.1)

Коэффициенты могут быть и другими.

В теории связи, в качестве модели помехи, часто используется случайный процесс, называемый белым шумом.

Белым шумом называется абсолютно случайный (дикий) процесс, энергетический спектр которого бесконечен и равномерен.

G(w)

G0 Рис.14.1.

0 w

G(w) = G₀ при 0 £ w ³ ¥

G₀ - спектральная плотность белого шума.

Мощность белого шума в полосе частот Dw (w в рад/с ) :

P = G₀*Dw

Пример белого шума - это тепловой шум. Функция корреляции белого шума вычисляется в соответствии с преобразованием Винера-Хинчина:

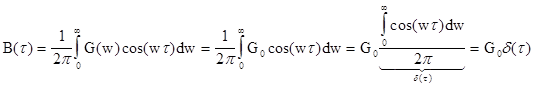
Функция корреляции белого шума имеет следующий вид:

В(t)

G0 d(t)

Рис.14.2.

0 t

Рассмотрим прохождение белого шума через полосовой фильтр. На входе идеального полосового фильтра с АЧХ равной :

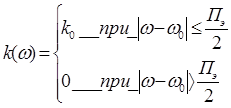
действует нормальный белый шум со спектральной плотностью G₀. Определим функцию корреляции и ФПВ процесса y на выходе фильтра; т.е. В(t)_вых и W(y) .

Спектр белого шума на входе фильтра показан на рис.14.1.

АЧХ полосового фильтра показана на рис. 14.2, а спектр процесса на выходе полосового фильтра изображен на рис.14.3.

К(w)

К0

0(w0 -Пэ/2) w0 (w0 +Пэ/2) w

Рис.14.2

G(w)вых

G0К0²

0(w0 -Пэ/2) w0 (w0 +Пэ/2) w

Рис.14.3.

Спектральная плотность белого шума на выходе ПФ: G(w)_вых = G₀К₀², т.к. АЧХ показывает во сколько раз изменится амплитуда напряжения, следовательно, энергия изменится в К₀² раз. В соответствии с соотношением Винера - Хинчина, зная G(w)_вых найдем В(t)_вых. :

График функции корреляции процесса на выходе ПФ показан на рис.14.4:

В(t)_вых

Рис.14.4.

t

-2p/Пэ 2p/Пэ

Определим ФПВ процесса у на выходе фильтра.

Т.к. процесс на входе фильтра нормальный с нулевым средним значением, то процесс y на выходе фильтра тоже будет гаусовским процессом с нулевым средним значением и дисперсией s², которая равна Bвых(0), как это указывалось в разделе , посвященном изучению функции корреляции:

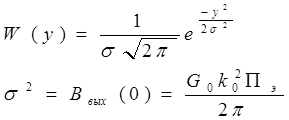
Анализ графика функции корреляции на рис.14.4 позволяет определить интервал корреляции для процесса на выходе фильтра. Интервал корреляции вычисляется в данном случае как расстояние от точки t =0 до значения t, при котором функция корреляции первый раз обращается в ноль. Из графика следует, что интервал корреляции равен 2p/п_э, т.е. обратно пропорционален ширине спектра процесса.

Вопросы для самопроверки.

1.Рассчитайте функцию корреляции случайного процесса , если известен его энергетический спектр.

2.Рассчитайте энергетический спектр процесса, если известна его корреляционная функция

3. Что такое белый шум?

4. Определите функцию корреляции случайного процесса на выходе полосового фильтра, если на входе фильтра действует белый щум.