Временная и спектральная диаграммы сигнала ЧМ

При ЧМ частота ВЧ колебания (несущей) изменяется в соответствии с НЧ модулирующим сигналом.

w_чм (t) = w₀ + DwU_нч(t), где (9.1)

w_чм (t)- частота ЧМ сигнала;

w₀- среднее значение несущей частоты;

U_нч(t)-модулирующий сигнал;

Dw-девиация частоты, т.е. максимальное отклонение частоты от среднего значения.

Если модулирующий сигнал гармонический, т.е.

U_нч = cosWt,

то w_чм(t) = w₀ + DwсоsWt

а выражение для ЧМ сигнала имеет вид:

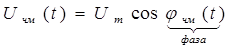
j_чм(t) =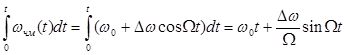

U_чм(t) = U_mcos(w₀t+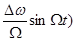

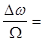M_ч - индекс ЧМ. (9.2)

U_чм(t) = U_mcos(w₀t+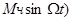

Временная диаграмма модулирующего сигнала имеет вид:

Uнч(t)

Рис.9.1.

t

Временная диаграмма соответствующего ЧМ сигнала принимает вид:

Uчм(t)

Рис.9.2

t

Как видно из рис.9.2, там, где модулирующий сигнал больше, там и частота ЧМ сигнала больше , а период колебаний меньше.

w_чм(t) = w₀ + DwcosWt

w_max = w₀ + Dw

w_min = w₀ - Dw

Амплитуда при ЧМ постоянна, меняется только частота.

Для получения спектра ЧМ сигнала разложим U_чм(t) в ряд Фурье.

U_чм(t) = U_mcos(w₀t+ 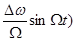= U_mÁ₀(M_ч)cosw₀t+ U_mÁ₁(M_ч)cos(w₀+W)t- U_mÁ₁(M_ч)cos(w₀W)t+U_mÁ₂(M_ч)cos(w₀+2W)t+U_mÁ₂(M_ч)cos(w₀2W)t+U_mÁ₃(M_ч)*cos(w₀+3W)t- U_mÁ₃(M_ч)cos(w₀-3W)t+¼

Á_k(M_ч) - функция Бесселя к-ого порядка.

Вид спектра зависит от М_ч.

Спектр ЧМ сигнала при М_ч<<1 (т.е. порядка 0,1; 0,05;¼)

u U_mнесущая

нижняяM_чU_m M_чU_m верхняя

боковая2 2боковая

w₀-W w₀ w₀+W w

Рис.9.3.

При М_ч<<1 спектр ЧМ сигнала похож на спектр АМ сигнала (несущая, 2 боковых ), но для ЧМ этот спектр приближенный. Все остальные боковые тоже есть, но они очень малы.

Спектр ЧМ сигнала при М_ч>1 выглядит так (Мч=5):

U J₄(Mч) J₄(Mч)

)

J₃(Mч) J₁(Mч) J₁(Mч) J₃(Mч) Рис.9.4.

J₅(Mч) J₂(Mч) J₀(Mч) J₂(Mч) J₅(Mч)

J₆(Mч) J₆(Mч) w

w₀-6W w₀-5W w₀-3W w₀-W w₀ w₀+W w₀+3W w₀+5W w₀+6W

w₀-4W w₀-2W w₀+2W w₀+4W

Полоса частот сигнала ЧМ.

П_чм @ 2W(М_ч+1)

М_ч<<1 П_чм @ 2W, ( как при АМ )

М_ч>>1 П_чм @ 2WМ_ч = 2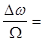W 2Dw

Ширина спектра при Мч>>1 не зависит от модулирующей частоты. Это широкополосный сигнал.