Методы уточнения корней
Отделение корней
Рассмотрим графический способ отделения корней уравнения (1), который используется, когда отсутствует информация о расположении корней. В интересующей нас области изменения неизвестного (интервал отделения) xÎ[x0, xn] вычислим ряд значений левой части уравнения (1) и результаты поместим в табл. 1, по которой можно построить график (рис. 1), из которого следует, что на данном интервале уравнение имеет 3 корня.
| Таблица 1 | |
| x | f (х) |
| x0 | f0 |
| x1 | f1 |
| … | … |
| xn | fn |
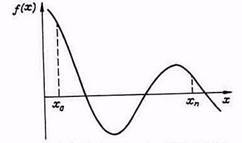
Рисунок 1. График левой части уравнения
Шаг изменения аргумента х при вычислении табл. 1 выбирается так, чтобы он был меньше расстояния между корнями. Только в этом случае удается отделить все корни.
Автоматизация нахождения интервалов изоляции основана на свойстве интервалов изоляции, заключающемся в различии знаков функции f (х) на их границах. Пример процедуры Roots, реализующей данный подход, приведен ниже. Параметры, передаваемые в процедуру:f-имя функции; а и б-границы интервала отделения;N-количество подинтервалов. Ниже приведен пример отделения корней для уравнения 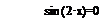 на отрезке [-0,1;6,5].
на отрезке [-0,1;6,5].
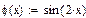
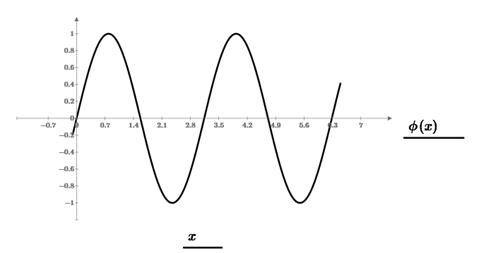
Из графика видно, что на данном интервале уравнение имеет 5 корней.
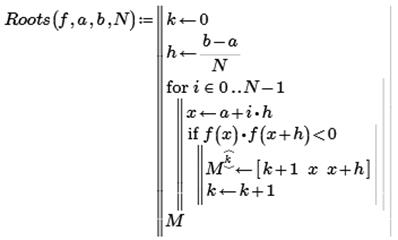
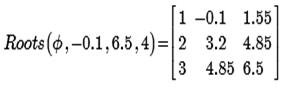
При четырех подинтервалах (крупном шаге) удалось отделить только 3 из 5 корней.
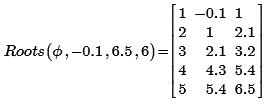
При шести подинтервалах (мелком шаге) удалось отделить все 5 корней.
Методы уточнения корней
Метод дихотомии
Считаем, что отделение корней уравнения (1) проведено и на интервале изоляции [а, b] расположен один корень, который необходимо уточнить с погрешностью e (рис. 2).
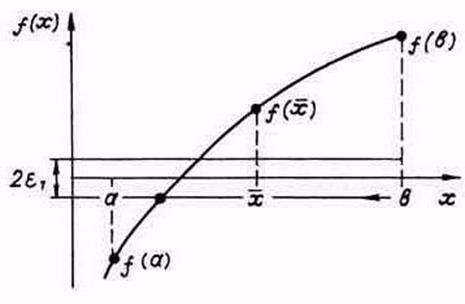
Рисунок 2. Метод дихотомии
Метод дихотомии, или половинного деления, заключается в следующем. Определяем середину отрезка [а, b]:  и вычисляем функцию
и вычисляем функцию 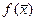 . Далее делаем выбор, какую из двух частей отрезка взять для дальнейшего уточнения корня. Если левая часть уравнения f(x) есть непрерывная функция аргумента х, то корень будет находиться в той половине отрезка, на концах которой f(x) имеет разные знаки. На рис. 3 это будет отрезок [а,
. Далее делаем выбор, какую из двух частей отрезка взять для дальнейшего уточнения корня. Если левая часть уравнения f(x) есть непрерывная функция аргумента х, то корень будет находиться в той половине отрезка, на концах которой f(x) имеет разные знаки. На рис. 3 это будет отрезок [а, 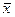 ], т.е. для очередного шага уточнения точку b перемещаем в точку
], т.е. для очередного шага уточнения точку b перемещаем в точку 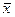 и продолжаем процесс деления как с первоначальным отрезком [а, b].
и продолжаем процесс деления как с первоначальным отрезком [а, b].
Итерационный (повторяющийся) процесс будем продолжать до тех пор, пока интервал [а, b] не станет меньше заданной погрешности e:
|xn-xn-1|<e
или когда значения функции f(x) (невязки) не станут достаточно малы
|f(xn)|<e1
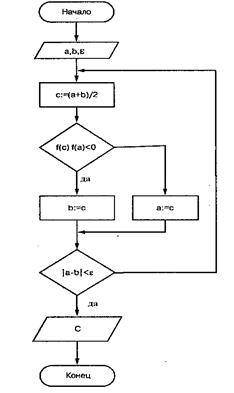
Рисунок 3. Алгоритм метода дихотомии
Дата добавления: 2020-04-12; просмотров: 662;











