Метод простых итераций

Классический метод

Исходное уравнение f(x)=0 всегда можно преобразовать к равносильному уравнению, прибавив к обеим его частям х

х = j(х) (2)

Пусть известно начальное приближение к корню х = x₀, тогда подставим его в правую часть уравнения (2) и получим новое приближение x₁ = j(х₀), затем аналогичным образом получим x₂ = j(х₁) и так далее. Таким образом, итерационное уравнение метода простых итераций имеет вид:

x_k+1 = j(х_k) (3)

Необходимо установить, при каких условиях итерационный процесс (3) будет сходиться к корню уравнения х*.

Построим графики двух функций:

y₁(x)=x

y₂(x)=j(x)

Координаты пересечения графиков этих функций и дадут корень исходного уравнения (1) х*.

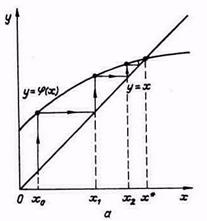
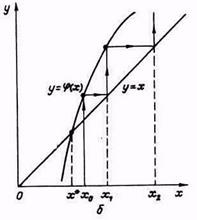
Рисунок. 4. Метод простых итераций:

а - сходящийся процесс ( );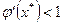

б - расходящийся процесс ( ).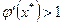

Рассмотрим процесс графически (рис.4). Из графиков видно, что возможны как сходящиеся, так и расходящиеся итерационные процессы. Для того чтобы итерационный процесс был сходящимся, должно выполняться условие

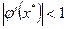(4)

Очевидно, классический метод не всегда обладает сходимостью, поэтому потребовалось его усовершенствование.

Усовершенствованный метод итераций

Умножим левую и правую части уравнения (1) на произвольную константу 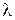и добавим к обеим частям неизвестное х. При этом корни исходного уравнения 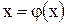не изменятся, где

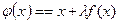(5)

Надлежащий выбор константы 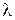позволит обеспечить выполнение условия сходимости (4). Необходимо выбрать величину 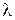такой, чтобы .

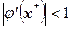Если функция j(х) выбрана в виде (5), то ее производная по х будет

j’(х) = 1+ 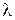f’(х)

Т.е. условие (4) имеет вид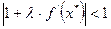

или

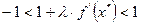
или

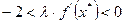
Поэтому константу 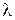необходимо выбирать из следующих условий:

А) если f’(х)>0

-2/f’(х*)< 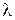<0

Б) если f’(х)<0

0< 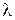<-2/f’(х*)

Наибольшую скорость сходимости получим при j’(х*)=0, тогда

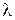= -1/f’(х*).Здесь х*-точка максимального значения модуля производной .

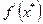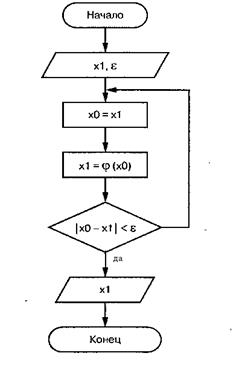
Рисунок 5. Алгоритм ре­шения методом простых итераций

Метод итераций обладает более высокой скоростью сходимости по сравнению с методом половинного деления.