Расчет элементов, подверженных действию осевой силы с изгибом
Расчет на прочность по нормальным напряжениям при действии момента и продольной силы выполняется для упругой и пластической стадий. Необходима также проверка устойчивости в плоскости действия момента, из плоскости действия момента и при косом внецентренном сжатии.
Расчет на прочность в упругой стадии ведется для эпюры напряжений в сечении 2-й стадии при пределе текучести стали 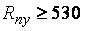 МПа при
МПа при 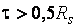 или
или 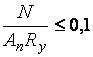 , а также при воздействии динамических нагрузок по формуле
, а также при воздействии динамических нагрузок по формуле
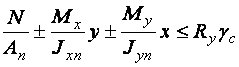 .
.
Внецентренно сжатые элементы из стали с 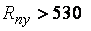 МПа с резко несимметричным сечением должны проверяться на прочность растянутых волокон (рис. 4.4)
МПа с резко несимметричным сечением должны проверяться на прочность растянутых волокон (рис. 4.4)
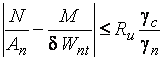 ,
,  ,
,
где d – учитывает увеличение момента из-за деформации; 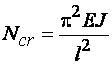 – определяется по упругой стадии [14];
– определяется по упругой стадии [14]; 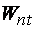 – для растянутого волокна.
– для растянутого волокна.

| Проверку прочности внецентренно сжатых,
сжато-изгибаемых и растянуто-изгибаемых элементов
из стали с пределом текучести до 530 МПа,
не подвергающихся непосредственному
воздействию динамических нагрузок при
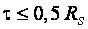 и и 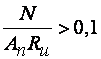 следует рассчитывать с учетом пластичности
материала (см. рис. 4.1, 4).
Рассмотрим этот расчет на примере прямоугольного
сечения в предельном состоянии – при развитии
пластичности по всему сечению.
Центрально приложенную силу и момент
(каждый в отдельности), вызывающие текучесть по
всему сечению, определяют по формулам:
следует рассчитывать с учетом пластичности
материала (см. рис. 4.1, 4).
Рассмотрим этот расчет на примере прямоугольного
сечения в предельном состоянии – при развитии
пластичности по всему сечению.
Центрально приложенную силу и момент
(каждый в отдельности), вызывающие текучесть по
всему сечению, определяют по формулам:
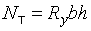 ; ; 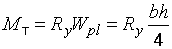 .
Момент и силу, вызывающие текучесть по всему
сечению при совместном действии, определим
из схемы (рис. 4.5) .
Момент и силу, вызывающие текучесть по всему
сечению при совместном действии, определим
из схемы (рис. 4.5)
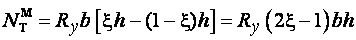 ; ;
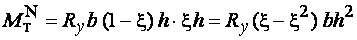 . .
|
Из схемы видно, что при равновесии сила 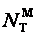 уравновешивает внешнюю силу N, пара сил
уравновешивает внешнюю силу N, пара сил 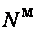 с плечом
с плечом 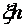 уравновешивает внешний момент М.
уравновешивает внешний момент М.
Составим выражение и преобразуем его:
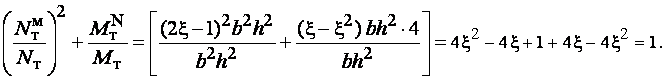
Если внешние силы меньше тех, которые сечение может воспринять в предельном состоянии, то равновесие сохраняется. После обратной подстановки получим условие прочности
 .
.
При действии N, 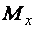 и
и 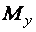 , по аналогии с предыдущим, можно
, по аналогии с предыдущим, можно
получить
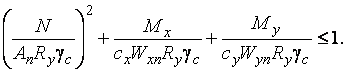
В общем виде (для любого сечения):
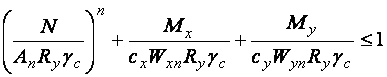 .
.
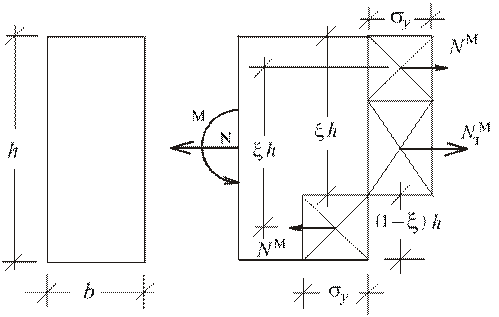
Рис. 4.5. Напряженное состояние стержня прямоугольного сечения при внецентренном растяжении в 4-й стадии
Значения n, а также с, 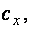
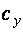 для разных типов сечений приводятся в [1, табл. 66]. Степень n учитывает распределение материала по высоте сечения. Для двутаврового сечения при изгибе относительно оси, перпендикулярной стенке, и коробчатого сечения, где значительная часть материала расположена на периферии,
для разных типов сечений приводятся в [1, табл. 66]. Степень n учитывает распределение материала по высоте сечения. Для двутаврового сечения при изгибе относительно оси, перпендикулярной стенке, и коробчатого сечения, где значительная часть материала расположена на периферии, 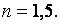 Для сечений, у которых значительная часть материала расположена в центре – крестовоеили двутавр – при изгибе относительно оси, проходящей по стенке,
Для сечений, у которых значительная часть материала расположена в центре – крестовоеили двутавр – при изгибе относительно оси, проходящей по стенке, 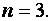 Для сечений, у которых материал расположен равномерно по высоте (прямоугольных),
Для сечений, у которых материал расположен равномерно по высоте (прямоугольных), 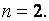
Расчет на устойчивость в плоскости действия момента при внецентренно сжатых и сжато-изгибаемых элементов постоянного сечения можно понимать как сохранение элементом прочности при расчете его с учетом деформаций системы от действующей нагрузки
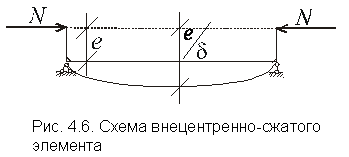
| 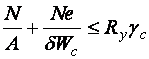 ,
где ,
где 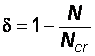 [14]; [14]; 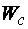 – момент
сопротивления сечения для наиболее сжатого волокна.
После простейших преобразований левой
части неравенства получим – момент
сопротивления сечения для наиболее сжатого волокна.
После простейших преобразований левой
части неравенства получим
|

где 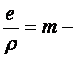 относительный эксцентриситет;
относительный эксцентриситет; 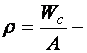 ядровое расстояние. Обозначим
ядровое расстояние. Обозначим 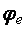 – коэффициент снижения расчетных сопротивлений при внецентренном сжатии. Учитывая, что при внецентренном сжатии предельное усилие
– коэффициент снижения расчетных сопротивлений при внецентренном сжатии. Учитывая, что при внецентренном сжатии предельное усилие 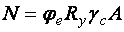 , и, сокращая площадь А, получим
, и, сокращая площадь А, получим
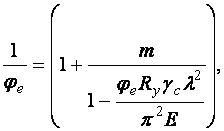 причем
причем 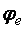 есть функция от
есть функция от 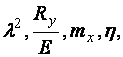
где h – коэффициент влияния формы сечения, определяется по [1, табл. 73].
Последнее уравнение имеет одно неизвестное – 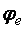 , и оно может быть найдено, если прочие величины известны. Но работать с функцией четырех аргументов неудобно. Для сокращения количества аргументов применим подстановки
, и оно может быть найдено, если прочие величины известны. Но работать с функцией четырех аргументов неудобно. Для сокращения количества аргументов применим подстановки 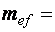
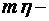 приведенный относительный эксцентриситет,
приведенный относительный эксцентриситет, 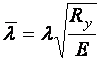 – условная гибкость. После введения новых переменных
– условная гибкость. После введения новых переменных 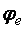 будет функцией двух переменных:
будет функцией двух переменных: 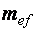 и
и 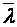 . Значения
. Значения 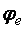 в зависимости от
в зависимости от 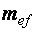 и
и 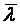 для сплошностенчатых стержней приводятся в [1, табл. 74].
для сплошностенчатых стержней приводятся в [1, табл. 74].
Формула для расчета внецентренно сжатых и сжато-изгибаемых элементов постоянного сечения принимает вид 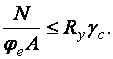
Это условие выполняется при 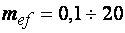 .
.
Расчет на устойчивость из плоскости действия момента элементов постоянного сечения при изгибе их в плоскости наибольшей жесткости 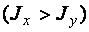 , совпадающей с плоскостью симметрии, ведется по формуле
, совпадающей с плоскостью симметрии, ведется по формуле
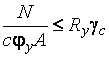 ,
,
где 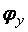 определяется как j
определяется как j 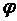 , но относительно оси у.
, но относительно оси у.
Коэффициент с при 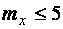 вычисляется по формуле
вычисляется по формуле
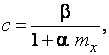
где 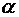 и
и 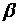 принимаются по [1, табл. 10];
принимаются по [1, табл. 10]; 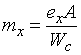 или
или 
При 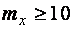 – по формуле
– по формуле
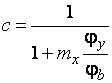 ,
,
где 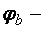 определяется как для балки с двумя и более закреплениями сжатого пояса по [1, прил. 7].
определяется как для балки с двумя и более закреплениями сжатого пояса по [1, прил. 7].
При 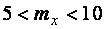
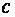 вычисляется по интерполяционной формуле
вычисляется по интерполяционной формуле
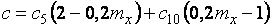 ,
,
где 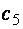 и
и 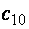 определяются при
определяются при 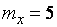 и
и 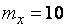 .
.
Расчет на устойчивость сплошностенчатых стержней при сжатии и изгибе в двух главных плоскостях, при совпадении плоскости наибольшей жесткости 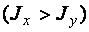 с плоскостью симметрии, следует выполнять по формуле
с плоскостью симметрии, следует выполнять по формуле
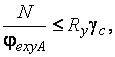
где 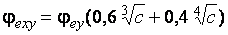 , здесь
, здесь 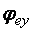 следует определять с заменой в формулах m и l на
следует определять с заменой в формулах m и l на 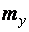 и
и 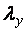 , а с определяется как раньше, но по
, а с определяется как раньше, но по 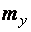 и
и 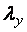 .
.
Дата добавления: 2016-05-30; просмотров: 3362;











