Расчет изгибаемых элементов

Проверяется прочность, устойчивость общая и местная, деформации. Изгиб может быть в одной и двух плоскостях (плоский и косой). Проверки могут делаться по упругой и упруго-пластической стадии работы материала. Поскольку сталь на начальной стадии работы наиболее близко подходит к идеально упругому телу, рассматриваемому в сопротивлении материалов, расчет часто ведется по формулам этой дисциплины или приведенным к ним.

При расчете на прочность в упругой стадии нормальные напряжения проверяются по 2-й стадии работы сечений (см. рис. 4.1).

Нормальные напряжения при плоском и косом изгибе проверяются по формулам:

.

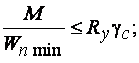
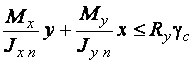Касательные напряжения проверяются по формуле Журавского

.

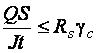При наличии отверстий вводится коэффициент 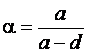, где а – шаг отверстий; d – диаметр отверстий.

При наличии местных напряжений 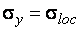(см. рис. 3.3) стенка балки проверяется по условию

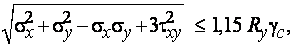
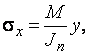
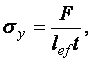
где 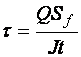, 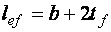; t – толщина стенки балки; 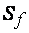– статический момент сечения пояса балки относительно ее центра тяжести; 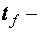толщина пояса проверяемой балки; b – ширина полки вышележащей балки; J – учитывается с коэффициентом а (см. выше).

Проверка общей устойчивости балки производится по формуле

,

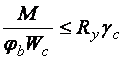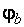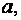
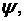
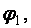
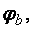
где принимается по [1, прил. 7], при этом последовательно определяются 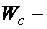для сжатого пояса.

При достаточной ширине сжатого пояса балки 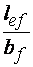меньше или равной предельных значений [1, табл. 8], либо при передаче нагрузки через сплошной жесткий настил, непрерывно опирающийся на сжатый пояс, – проверки общей устойчивости можно не делать ( 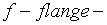пояс балки).

Проверка деформаций при плоском и косом изгибах выполняется по формулам:

, .

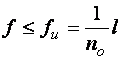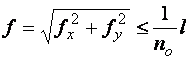Деформации определяются от воздействия моментов по нагрузкам с коэффициентом .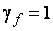

Расчет на прочность при пластической работе материала может выполняться для разрезных балок сплошного постоянного сечения из сталей с пределом текучести до 530 МПа, несущих статическую нагрузку. Он ведется по 3-й стадии, когда в сечении имеется упругое ядро. В балках переменного сечения расчет с развитием пластических деформаций допускается только для одного, наиболее загруженного сечения.

Положение нейтральной оси в этом случае определяется из условия :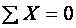

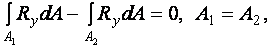
нейтральная ось делит площадь сечения пополам. Воспринимаемый сечением момент найдем из условия

, ,

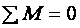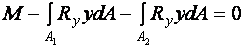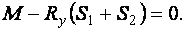
Обозначим 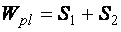, тогда 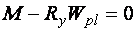и

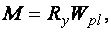
где 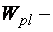пластический момент сопротивления.

Вычислим его для прямоугольного сечения:

.

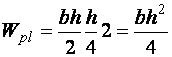Найдем соотношение между пластическими упругим моментами сопротивления:

,

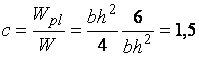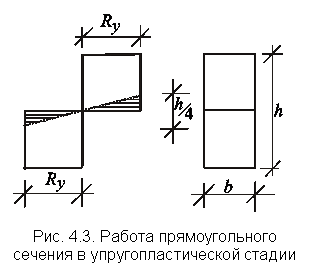
отсюда 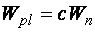. Но сечение по 4-й стадии работать не может, пластические деформации стали ограничены. Для ограничения больших деформаций необходимо упругое ядро. Допустим полные деформации в 4 раза больше упругих, т. е. упругое ядро сечения имеет высоту, равную 1/4 h (рис. 4.3). Потеря в моменте сопротивления

,

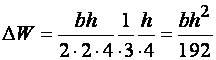что в относительных единицах составляет

.

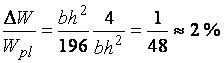С учетом наличия упругого ядра 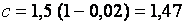, что и приведено в [1, табл. 66] для прямоугольного сечения. Там же даются значения 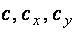и для других наиболее распространенных сечений. Расчет на прочность разрезных балок сплошного сечения по упруго-пластическому моменту сопротивления, на нагрузку, действующую в одной из главных плоскостей, следует выполнять по формулам: 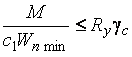, 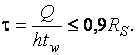На косой изгиб расчет по пластическим моментам сопротивления следует выполнять по формуле .

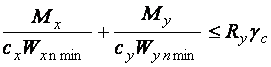При тех же условиях и 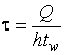≤ 0,5 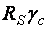. Здесь 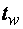– толщина стенки, h – высота.

Расчет опорных сечений балок в этих случаях (пр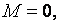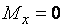и и 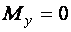) следует выполнять по формуле .

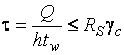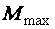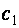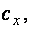
При наличии зоны чистого изгиба ( на значительной длине) , 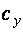заменяются на 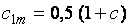, 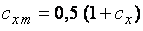и 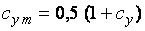( 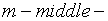среднее значение).

При одновременном действии в сечении момента M и поперечной силы Q коэффициент с₁ следует определять по формулам:

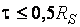
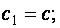при при 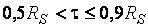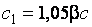, где

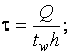
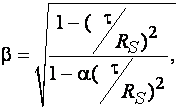
здесь а – коэффициент, равный 0,7 для двутаврового сечения, изгибаемого в плоскости стенки, и 0 – для других типов сечений; с – коэффициент, принимаемый по [1, табл. 66]; с₁ – коэффициент, принимаемый не менее 1 и не более коэффициента с.