Расчет центрально-растянутых элементов
Проверяется прочность по ослабленному сечению 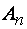 и гибкость:
и гибкость:
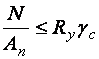 .
.
Там где возможна эксплуатация конструкций и после достижения материалом 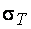 и
и 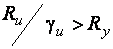 , проверку следует выполнять по формуле
, проверку следует выполнять по формуле
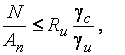
где 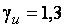 .
.
Гибкость 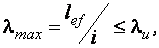
где 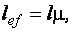 (
(  действительный);
действительный); 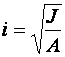 – радиус инерции. Значения m для ферм приводятся в [1, табл. 11 и 12] , предельные гибкости
– радиус инерции. Значения m для ферм приводятся в [1, табл. 11 и 12] , предельные гибкости 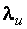 – в [1, табл. 20] для растянутых элементов в зависимости от типа нагрузок и вида конструкций. Значения m и i следует подбирать так, чтобы гибкость получалась максимальной.
– в [1, табл. 20] для растянутых элементов в зависимости от типа нагрузок и вида конструкций. Значения m и i следует подбирать так, чтобы гибкость получалась максимальной.
4.3. Расчет центрально-сжатых элементов [6, 8]
Расчет на прочность выполняется только по расчетным сопротивлениям, определенным по пределу текучести. Гибкость проверяется так же, как и при центральном растяжении:
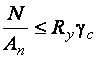 ,
, 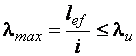 ,
, 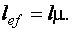
где 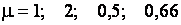 – для шарнирного закрепления стержня на опорах соответственно жесткого закрепления на одной опоре; жесткого закрепления стержня с двух сторон; жесткого закрепления с одной и шарнирно-неподвижного с другой стороны. Предельная гибкость
– для шарнирного закрепления стержня на опорах соответственно жесткого закрепления на одной опоре; жесткого закрепления стержня с двух сторон; жесткого закрепления с одной и шарнирно-неподвижного с другой стороны. Предельная гибкость 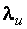 находится в зависимости от степени использования несущей способности стержней
находится в зависимости от степени использования несущей способности стержней 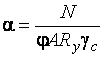 , принимаемой не менее 0,5. Для разных стержней
, принимаемой не менее 0,5. Для разных стержней 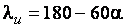 или
или 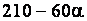 , или
, или 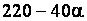 [1, табл. 19].
[1, табл. 19].
Расчет на устойчивость.
Идеально центральное сжатие невозможно из-за неточности монтажа, несовершенства расчетной схемы, других случайных причин и потери прямолинейной формы перед разрушением. Поэтому устойчивость сохраняется, если
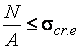 ,
,
где 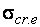 – критические напряжения при внецентренном сжатии.
– критические напряжения при внецентренном сжатии.
Обозначим
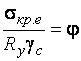 .
.
Тогда 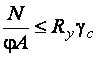 ,
,
где коэффициент устойчивости можно представить в виде произведения двух коэффициентов: 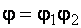 , отдельно учитывающих:
, отдельно учитывающих:
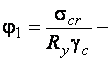 потерю устойчивости при строго центральном сжатии;
потерю устойчивости при строго центральном сжатии;
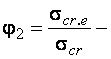 влияние случайного эксцентриситета на устойчивость сжатого стержня (
влияние случайного эксцентриситета на устойчивость сжатого стержня ( 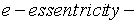 эксцентриситет).
эксцентриситет).
При 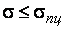 материал работает упруго, критические напряжения определяются по формуле Эйлера
материал работает упруго, критические напряжения определяются по формуле Эйлера
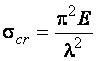 .
.
До гибкости 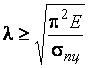 сохраняется прямолинейная форма устойчивости (до
сохраняется прямолинейная форма устойчивости (до 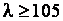 – для С235).
– для С235).
При 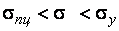 по случайным причинам (неидеальная статическая схема, неточности монтажа и т. п.) теряется прямолинейная форма, стержень искривляется, появляется эксцентриситет, и в опасном сечении появляется момент
по случайным причинам (неидеальная статическая схема, неточности монтажа и т. п.) теряется прямолинейная форма, стержень искривляется, появляется эксцентриситет, и в опасном сечении появляется момент 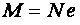 (рис. 4.2)
(рис. 4.2)
.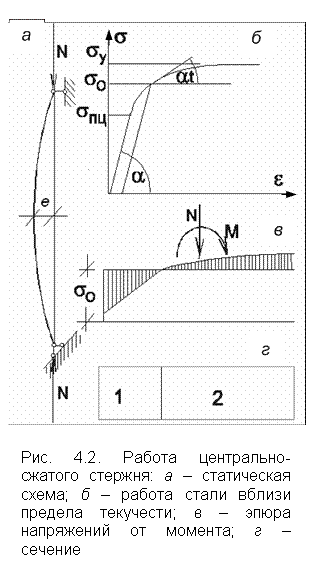
Криволинейная форма устойчивости некоторое время может сохраняться. Сила 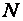 создает в опасном сечении равномерные напряжения от сжатия
создает в опасном сечении равномерные напряжения от сжатия 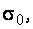 к которым добавляется двузначная эпюра напряжений от момента (рис. 4.2, в).
к которым добавляется двузначная эпюра напряжений от момента (рис. 4.2, в).
Напряжения от момента догружают более сжатые волокна с модулем
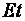 (зона сечения 2) и разгружает менее загруженные с модулем E (зона сечения 1), где
(зона сечения 2) и разгружает менее загруженные с модулем E (зона сечения 1), где 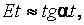
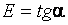 (рис. 4.2, б и г).
(рис. 4.2, б и г).
При этом угол 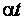 определяется касательной к диаграмме
определяется касательной к диаграмме 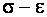 в точке с напряжениями
в точке с напряжениями 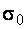 и является переменной величиной, как и модуль
и является переменной величиной, как и модуль 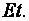
При изгибе кривизна нейтрального слоя от воздействия М
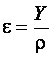 ;
; 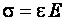 ;
; 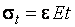 .
.
Из условия равенства усилий в сжатой и растянутой зонах при изгибе
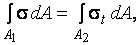 ,
, 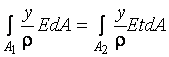 ,
, 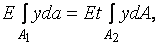
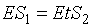 .
.
При стандартизованной для конкретной стали диаграмме 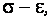 заданном значении
заданном значении 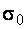 и определенной форме сечения – это уравнение с одним неизвестным, из которого находится координата
и определенной форме сечения – это уравнение с одним неизвестным, из которого находится координата 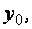 определяющая положение нейтрального слоя при изгибе. Далее из условия равенства внешнего момента и уравновешивающих его внутренних сил
определяющая положение нейтрального слоя при изгибе. Далее из условия равенства внешнего момента и уравновешивающих его внутренних сил
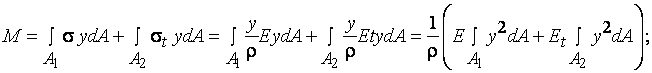
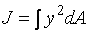 ;
; 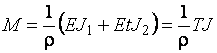 . По аналогии
. По аналогии 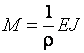 для упругой стадии работы. Обозначим через
для упругой стадии работы. Обозначим через 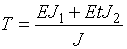 приведенный модуль Энгессера–Ясинского, где
приведенный модуль Энгессера–Ясинского, где 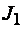 и
и 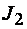 – моменты инерции, разгруженной моментом (рис. 4.2, сеч. 1) и догруженной моментом (рис. 4.2, сеч. 2) относительно общего слоя. Тогда аналогично решению Эйлера:
– моменты инерции, разгруженной моментом (рис. 4.2, сеч. 1) и догруженной моментом (рис. 4.2, сеч. 2) относительно общего слоя. Тогда аналогично решению Эйлера: 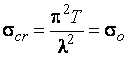 ,
, 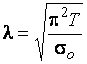 .
.
Значения 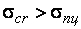 при прямолинейной и криволинейной формах очень близки, криволинейная форма устойчивости быстро ведет к разрушению при росте
при прямолинейной и криволинейной формах очень близки, криволинейная форма устойчивости быстро ведет к разрушению при росте 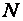 .
.
Значение  находят на основе статистического исследования случайных эксцентриситетов (и погнутого в том числе). Эксцентриситеты эти растут с ростом гибкости, оставаясь малыми. Учет влияния этих неблагоприятных факторов на устойчивость центрально-сжатых элементов ведется на основе анализа работы внецентренно сжатых элементов, работающих с малыми эксцентриситетами.
находят на основе статистического исследования случайных эксцентриситетов (и погнутого в том числе). Эксцентриситеты эти растут с ростом гибкости, оставаясь малыми. Учет влияния этих неблагоприятных факторов на устойчивость центрально-сжатых элементов ведется на основе анализа работы внецентренно сжатых элементов, работающих с малыми эксцентриситетами.
В СНиП [1, табл. 72] даются готовые коэффициенты: 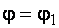 ×
× 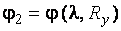 , а также формулы для вычисления j в зависимости от условной гибкости:
, а также формулы для вычисления j в зависимости от условной гибкости:
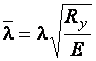
для любых сечений.
При 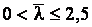
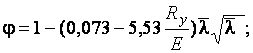
при 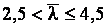
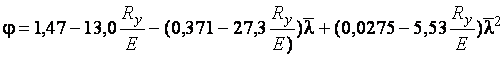 ;
;
при 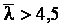
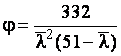 .
.
Дата добавления: 2016-05-30; просмотров: 4250;











