Числовые характеристики непрерывных случайных величин.

Распространим определения числовых характеристик случайных величин на непре-рывные случайные величины, для которых плотность распределения служит в некото-ром роде аналогом понятия вероятности.

Определение.Математическим ожиданием (средним значением по распределению) называется действительное число, определяемое в зависимости от типа СВ Х формулой: m_X = M[X] =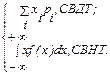

Для непрерывной случайной величины называется 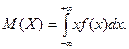Замечание 1. Общее определение дисперсии сохраняется для непрерывной случайной величины таким же, как и для дискретной, а формула для ее вычисления имеет вид: 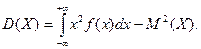Среднее квадратическое отклонение вычисляется по формуле

Замечание 2. Если все возможные значения непрерывной случайной величины не выходят за пределы интервала [a, b], то интегралы в формулах и вычисляются в этих пределах.

Пример. Плотность распределения случайной величины Х имеет вид:

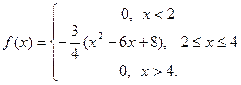
Найти М(Х), D(X), σ.

Решение.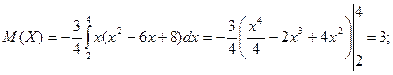

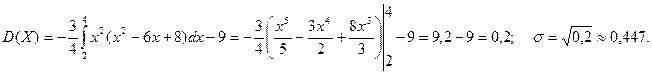Свойства математического ожидания:

1. M[C] = C, где С - константа;

2. M[C×X] = C×M[X];

3. M[X+Y] = M[X]+M[Y], для любых СВ X и Y;

4. M[X×Y] = M[X]×M[Y] + K_XY, где K_XY = M[ 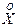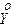] - ковариация СВ X и Y.

Начальным моментом k-го порядка (k = 0, 1, 2, ...) распределения СВ Х называется действительное число, определяемое по формуле:

n_k = M[X^k] =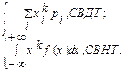

Центральным моментом k-го порядка распределения СВ Х называется число, определяемое по формуле:

m_k = M[(X-m_X)^k]=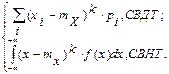

Из определений моментов, в частности, следует, что: n₀ = m₀ = 1, n₁ = m_X, m₂ = D_X = s_X².

Модой СВНТ называется действительное число Mo(X) = x*, определяемое как точка максимума ПР f(x). Мода может иметь единственное значение (унимодальное распределение) или иметь множество значений (мультимодальное распределение).

Медианой СВНТ называется действительное число Mе(X) = x₀, удовлетворяющее условию: P{X < x₀} = P{X ³ x₀} или F(x₀) = 0,5.

Квантилем уровня р называется действительное число t_p, удовлетворяющее уравнению: F(t_p) = p. В частности, из определения медианы следует, что x₀ = t_0,5.

Дисперсией СВ Х называется неотрицательное число D[X] = D_Х, определяемое формулой:

D_X = M[(X-m_X)²] = M[X²] - m_X² =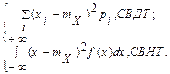

Дисперсия существует, если ряд (соответственно интеграл) в правой части равенства сходится. Свойства дисперсии:

1. D[C] = 0, где С - константа;

2. D[C×X] = C²×D[X];

3. D[X-C] = D[X], дисперсия, очевидно, не меняется от смещения СВ X;

4. D[X + Y] = D[X] + D[Y] + 2×K_XY, где K_XY = M[ 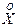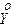] - ковариация СВ X и Y;

5.

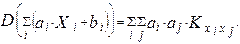
Неотрицательное число s_Х = 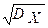называется среднеквадратичным отклонением СВ X. Оно имеет размерность СВ Х и определяет некоторый стандартный среднеквадратичный интервал рассеивания, симметричный относительно математического ожидания. (Величину s_Х иногда называют стандартным отклонением). СВ Х называется стандартизованной, если m_X = 0 иs_Х = 1. Если величина Х = const (т.е. Х не случайна), то D[X] = 0.

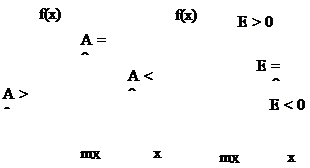
Показателем асимметрии ПР является коэффициент асимметрии (“скошенности”) распределения: A = m₃/s³_X. Показателем эксцесса ПР является коэффициент эксцесса (“островершинности”) распределения: E = (m₄/s⁴_X)-3. В частности, для нормального распределения E = 0.