Лекция 6 Непрерывная случайная величина

(Тема 4.1.)

План лекции

Понятие непрерывной случайной величины.

Функция плотности непрерывной случайной величины: определение, свойства.

Интегральная функция распределения непрерывной случайной величины: определение, свойства, её связь с функцией плотности.

Методика расчета вероятностей для НСВ по её функции плотности и интегральной функции распределения.

Математическое ожидание, дисперсия и среднеквадратическое отклонение. Медиана и мода непрерывной случайной величины.

Определение и свойства функции распределения сохраняются и для непрерывной случайной величины, для которой функцию распределения можно считать одним из видов задания закона распределения. Но для непрерывной случайной величины вероятность каждого отдельного ее значения равна 0. Это следует из свойства 4 функции распределения: р(Х = а) = F(a) – F(a) = 0. Поэтому для такой случайной величины имеет смысл говорить только о вероятности ее попадания в некоторый интервал.

Вторым способом задания закона распределения непрерывной случайной величины является так называемая плотность распределения (плотность вероятности, дифференциальная функция).

Определение 5.1. Функция f(x), называемая плотностью распределениянепрерывной случайной величины, определяется по формуле:

f (x) = F′(x), (5.1)

то есть является производной функции распределения.

Свойства плотности распределения.

1) f(x) ≥ 0, так как функция распределения является неубывающей.

2) 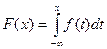, что следует из определения плотности распределения.

3) Вероятность попадания случайной величины в интервал (а, b) определяется формулой 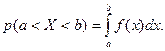Действительно,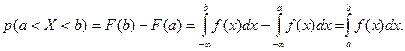

4) 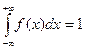(условие нормировки). Его справедливость следует из того, что 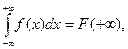а

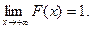
5) 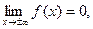так как 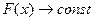при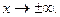

Таким образом, график плотности распределения представляет собой кривую, расположенную выше оси Ох, причем эта ось является ее горизонтальной асимптотой при 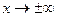(последнее справедливо только для случайных величин, множеством возможных значений которых является все множество действительных чисел). Площадь криволинейной трапеции, ограниченной графиком этой функции, равна единице.

Замечание. Если все возможные значения непрерывной случайной величины сосредоточены на интервале [a, b], то все интегралы вычисляются в этих пределах, а вне интервала [a, b] f(x) ≡ 0.

Пример 1. Плотность распределения непрерывной случайной величины задана формулой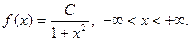

Найти: а) значение константы С; б) вид функции распределения; в) p(-1 < x < 1).

Решение. а) значение константы С найдем из свойства 4:

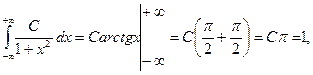откуда .

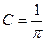б)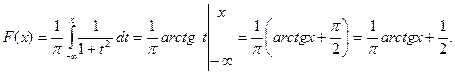

в)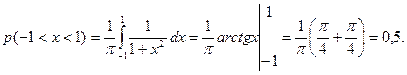

Пример 2. Функция распределения непрерывной случайной величины имеет вид:

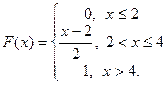
Найти плотность распределения.

Решение.

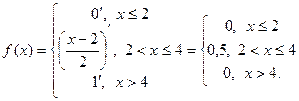
Пример 3. Могут ли функции j(x) и y(x) являться ФР или ПР некоторой СВ X, если “да”, то при каком значении l?

а) j(x) =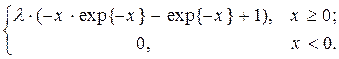

б) y(x) =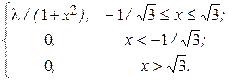

Различают следующие группы числовых характеристик: характеристики положения (математическое ожидание, мода, медиана, квантиль и др.), рассеивания (дисперсия, среднеквадратичное отклонение и др.), характеристики формы плотности распределения (показатель асимметрии, эксцесса и др.).