Решение задач методом редукции

Этот метод приводит к хорошим результатам потому, что часто решение задач имеет иерархическую структуру. Не обязательно требовать, чтобы основная задача и все её под-задачи решались одинаковыми методами. Редукция полез-на для представления глобальных аспектов задачи, а при решении более специфичных задач предпочтителен метод планирования по состояниям. Метод планирования по состояниям можно рассматривать как частный случай метода планирования с помощью редукций, ибо каждое применение оператора в пространстве состояний означает сведение исходной задачи к двум более простым, из которых одна является элементарной.

В общем случае редукция исходной задачи не сводится к формированию таких двух подзадач, из которых хотя бы одна была элементарной.

Поиск планирования в пространстве задач заключается в последовательном сведении исходной задачи к всё более простым до тех пор, пока не будут получены только элемен-тарные задачи. Частично упорядоченная совокупность та-ких задач составит решение исходной задачи. Расчленение задачи на альтернативные множества подзадач удобно пред-ставлять в виде И/ИЛИ-графа. В таком графе всякая вер-шина, кроме концевой, имеет либо конъюнктивно связан-ные дочерние вершины (И-вершина), либо дизъюнктивно связанные (ИЛИ-вершина).

В частном случае, при отсутствии И-вершин, имеет место граф пространства состояний. Концевые вершины являют-ся либо заключительными (им соответствуют элементар-ные задачи), либо тупиковыми. Начальная вершина (корень И/ИЛИ-графа) представляет исходную задачу. Цель поиска на И/ИЛИ-графе – показать, что начальная вершина разре-шима. Разрешимыми являются заключительные вер-шины(И-вершины), у которых разрешимы все дочерние вершины, и ИЛИ-вершины, у которых разрешима хотя бы одна дочерняя вершина. Разрешающий граф состоит из разрешимых вершин и указывает способ разрешимости начальной вершины. Наличие тупиковых вершин приводит к неразрешимым вершинам.

Неразрешимыми являются тупиковые вершины, И-верши-ны, у которых неразрешима хотя бы одна дочерняя верши-на, и ИЛИ-вершины, у которых неразрешима каждая дочер-няя вершина.

Примеры: Алгоритм Ченга и Слейгла, Метод ключевых операторов, Метод планирования общего решателя задач (ОРЗ), Дедуктивный метод планирования системы QA3, ОРЗ не оправдал возлагавшихся на него надежд в основном из-за неудовлетворительного представления задач. Попытка исправить положение привела к созданию вопросно-ответ-ной системы QA3, Метод продукций системы STRIPS, Ме-тод продукций, использующий макрооператоры [Файкс и др., 1973]. Макрооператоры – это обобщенные решения задач, получаемые методом STRIPS.

Для большего понимания рассмотренных выше положений (продукционные модели знаний, И/ИЛИ-граф) проанализируем пример [Смолин В.Д.].

Есть четыре абстрактных населённых пункта А, B, C, D, связанные дорогами. Причём дороги связывают следующие пункты: A -> B, B -> C, B -> D, C -> D.

Переведём данную постановку задачи в термины продук-ционной модели представления знаний.

Сформируем раздел «Факты»:

дорога (A,B);

дорога (B,C);

дорога (B,D);

дорога (C,D).

Раздел «Правила»:

прежде всего введём правило «прямой дороги», затем правило «транзитная дорога» и правило наличия любой дороги «есть дорога».

прямая дорога (X,Y), если дорога (X,Y) или дорога (Y,X);

транзитная дорога(X,Y), если дорога (X,Z) и дорога (Z,Y);

есть дорога(X,Y), если прямая дорога (X,Y) или транзитная дорога (X,Y).

Какую же задачу можно решить при помощи такой БЗ и соответствующей фактуры?

Обратимся к ИНТСИС на базе нашей продукционной модели: есть ли дорога между пунктами A и D?

Ход решения

1 – На вход МВ пользователь подаёт цель «Есть дорога (A,D)».

2 – МВ осуществляет поиск текстовой строки в файле БЗ.

3 – МВ загрузит запрос в стек целей(структура для хранения данных, которая работает по принципу LIFO или «последний вошёл – первый вышел») и приступит к поиску цели «Прямая дорога».

4 – МВ загрузит в стек целей цель «Прямая дорога» и приступит к поиску цели «Дорога».

5 – МВ просматривает все текстовые строки «Дорога» в разделе «Факты» и обнаружит, что искомой строки «Дорога (A,D) среди них нет.

6 – МВ выгрузит из стека цели «Дорога», «Прямая дорога», «Есть дорога». Раскроет цель «Есть дорога» и начнёт поиск цели «Транзитная дорога». Перед этим загрузив в стек цель «Есть дорога».

7 – Цель «Транзитная дорога» будет удовлетворена, так как на самом деле есть дорога «A -> B -> D».

Этот пример иллюстрирует так называемый «обратный вывод», т.е., мы идём от цели для её подтверждения к данным. Прямой вывод применялся, если бы требовалось породить все возможные на данной карте маршруты.

Тогда цель была бы сформулирована как «Дорога (X,Y)». Напоминая это в нотации, близкой ПРОЛОГу.

Алгоритмический поиск решения или поиск, имитиру-ющий мышление, есть примитивный поиск подстроки в строках фактов исходной БД в цикле до первого решения или совпадения. Графическое или точнее графовое пред-ставление задачи значительно упрощает решение и де-лает его более экономным.

Более подробно саму концепцию решения задач мето-дом поиска в пространстве состояний мы рассматривали на 6-й лекции.

Как видно из рисунка возмож-ны два решения нашей задачи:

A – B – D

A – B – C – D

Эти записи называют «путь решения задачи». Первый явно короче, но проблема в том, что находясь в начальной точке, мы об этом не знаем.

Вершину А называют «кор-нем дерева», «целевой верши-ной» или «глобальной целью».

Вершины В и С – вычисляе-мыми (раскрываемыми, проме-жуточными) вершинами.

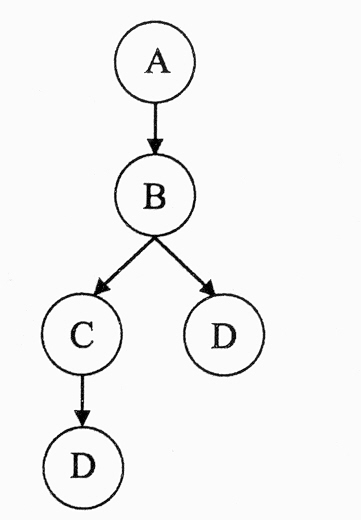Вершину D – терминальной или завершающей.

Рёбра, соединяющие вершины, выступают в качестве присоединённых процедур. Они должны выполняться для реализации перехода в следующую вершину (состояние). Придумайте пример с постановкой диагноза и неис.авто.

Рассмотрим структуру задач искусственного интеллекта, а значит и ИНТСИС. Структура задачи представима в виде своеобразной пирамиды. Снизу вверх или от основания к вершине: МОНИТОРИНГ, АНАЛИЗ, ПРОГНОЗИРОВА-НИЕ, УПРАВЛЕНИЯ. Эти этапы достаточно обобщённые и универсальные. Они совпадают с этапами системного иссле-дования. Можно, например, выделить такие пары: МОНИ-ТОРИНГ-ПРЕДПРОЕКТНОЕ ОБСЛЕДОВАНИЕ; ПРОГНО-ЗИРОВАНИЕ-РАБОТА С МАТМОДЕЛЬЮ; УПРАВЛЕНИЕ-РЕШЕНИЕ ПРОБЛЕМЫ.

Иерархическая структура задач ИИ

Для решения задачи необходимо:

v уточнить её для конкретной предметной области;

v выбрать необходимые параметры решения: точность ре-зультатов, надёжность результатов (способность системы мало изменять значения своих выходов при малых измене-ниях входов на сериях испытаниях), время решения и т.д.

Уточнение задачи – этап, который не зависит от выбран-ной модели решения или представления знаний. При этом думают о природе задачи, а не о способах её решения. Важ-но так уточнить задачу, чтобы она стала «узкой» от нашего уточнения (что требуется делать и какую цель достичь), но при этом оставалась достаточно «широкой» в смысле плана действий.

Эти требования к решению задач противоречивы (привет от СА). Их системное объединение хорошо показывается на примере абстрактных задач: обработка списков, обоснова-ние гипотез и т.д.

Первым по важности параметром является точность ре-шения. Для физических систем существует метрическая сис-тема единиц: килограммы, метры и т.п. Для интеллектуаль-ных систем общепринятой методики и единиц измерения нет. Обычно говорят о проценте правильных решений и т.п. Например, для медицинских систем хорошей считается си-туация, в которой получают 70 % и более правильной поста-новки диагноза при первом осмотре больного.

Второй параметр – устойчивость (требования к надёж-ности) – касается поведения системы при её широких испы-таниях в разных условиях.

Третий параметр – экономичность. Экономичным решение признаётся, исходя из некоторой точки зрения или по некоторому критерию. Чаще всего имеют в виду время решения и стоимость решения. Либо обратный вариант – стоимость ошибки.

Вернёмся к решению задач методами полного пере-бора и рассмотрим их достаточно детально. Процесс применения присоединённых процедур называют по-рождением вершин или перебором вариантов. При по-рождении новой вершины обязательно запоминается указатель на старую. Перебор завершается составлени-ем множества этих указателей, называемого путём ре-шения задачи.

От того, как раскрывают каждую возможную «веточку» дерева целей: сразу до терминальных фактов или только на некоторую заданную глубину различают две основные стратегии слепого перебора – «в ширину»и «в глубину». Слепой перебор означает, что расположение целевой вер-шины не влияет на порядок раскрытия.

В первом случае (в ширину) вершины раскрываются в том же порядке, в котором они порождаются. Во вто-ром случае (в глубину) на каждом шаге первой раскры-вается вершина, которая была построена последней.

Есть случаи, когда существует некоторая допинформация о предметной области, позволяющая судить о характере графа пространства состояний и расположения цели, тогда говорят об эвристическом поиске.

Со словом «Эврика!» связана легенда про Архимеда. Оно означает «Открыл, нашёл». Поэтому «эвристичес-кий» значит «помогающий, служащий открытию». Эв-ристическая информация, опирающаяся, как правило, на предыдущий опыт, даёт возможность искать на графе (и не только) в наиболее перспективных направлениях.

Под графом будем понимать один наиболее простой его тип – дерево. У него каждая вершина имеет только одну вершину, непосредственно предшествующую ей. Это родительская вершина. За исключением вершины-корня, у которой предшествующих вершин нет.

МЕТОД ПОЛНОГО ПЕРЕБОРА В ШИРИНУ

Вершины раскрываются в том порядке, в котором они строятся (рис. на след. слайде). Базовый алгоритм состоит в выполнении следующих шагов.

1.Начальная вершина раскрывается до тех пор, пока её можно раскрыть, применяя один и тот же оператор. Так образуются вершины первого уровня S2, S3… Они раскрываются в свою очередь и образуются вершины второго уровня и т.д.

2.Расставляются указатели, ведущие от новых вер-шин к корню.

Указателями могут быть имена, буквы, цифры, имена операторов, расстоя-ния, стоимость, вес и т.д.

3.Проверятся, нет ли среди полученных вершин целевой. Если есть, то формируется решение на основе соответствующего оператора. Если нет, то

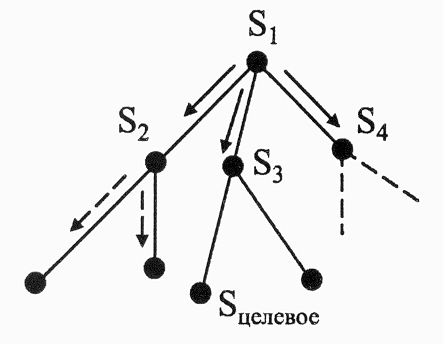рассматривается первая порождённая вершина и к ней применяется тот же алгоритм. После чего переходят ко вто-рой и т.д., пока среди получаемых вершин не окажется целе-вой.