Испарение бинарного раствора.

Может проводиться без отбора получившегося пара или с непрерывным отбором пара.

1) Без отбора

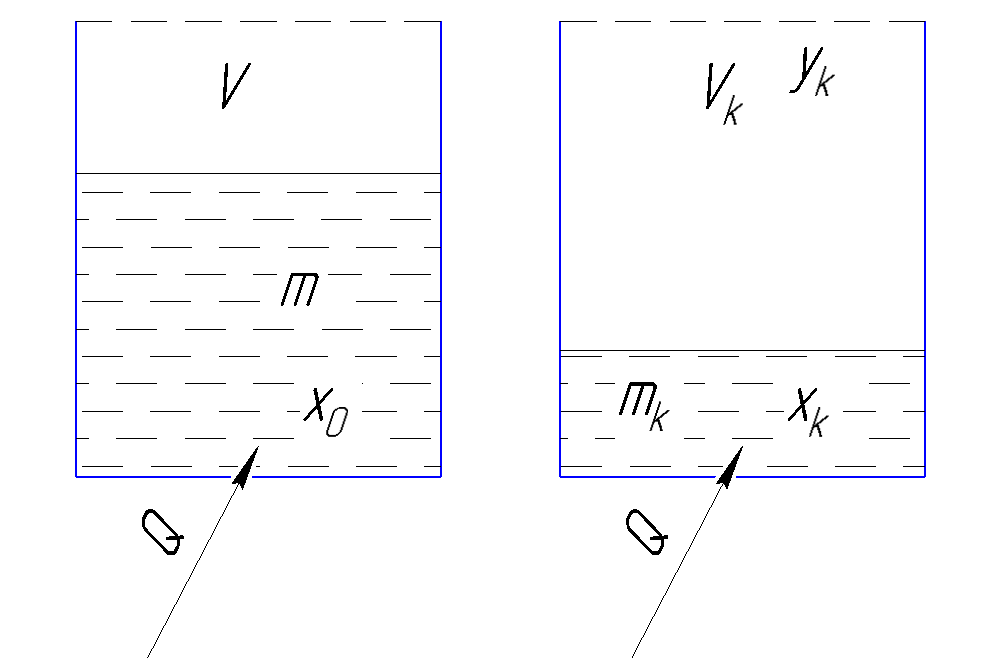
Рисунок 184. Испарение бинарного раствора.

m – количество жидкости;

V – количество пара;

x₀ – начальная концентрация низкокипящего компонента в жидкой фазе.

В процессе испарения количество жидкости уменьшается, количество пара возрастает. Поскольку пар не отводится, то общее кол-во пара и жидкости остается постоянным.

Зависимость количества жидкости от концентрации (мольной доли) определяется из уравнения материального баланса по низкокипящему компоненту в начале и в конце процесса.

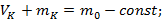
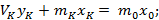
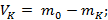
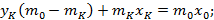
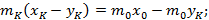
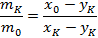
Рассмотрим изменения концентраций низкокипящего компонента.

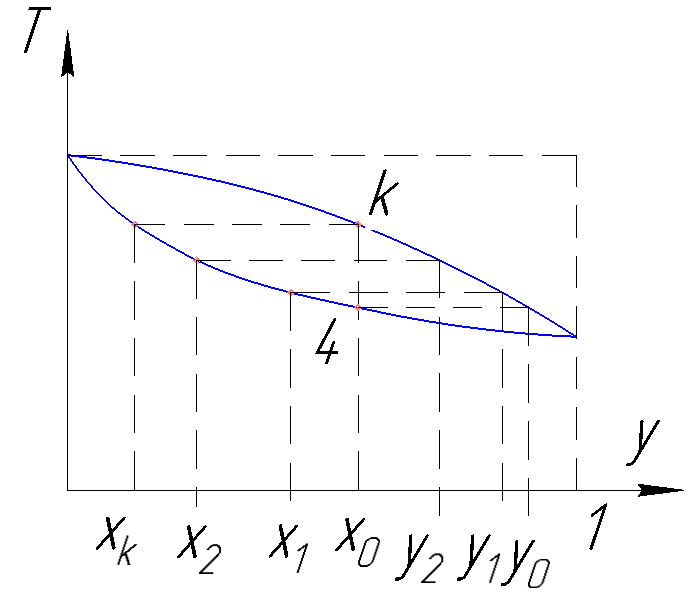
Рисунок 185. Испарение бинарного раствора.

1) В начальный момент кипения имеем максимальное кол-во низкокип.комп.в паре;

2)

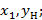
3) С течением времени при кипении концентрация низкокипящего компонента в паровой и жидкостной фазах уменьшается.

В конечной точке, когда последняя капля превращается в пар, имеем наинизшую концентрацию низкокипящего компонента в последних каплях жидкости.

Например, для воздуха, как бинарная смесь:

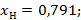
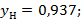
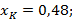
=> получать чистые продукты без отвода пара невозможно, поскольку концентрации низкокипящего компонента в начале процесса в жидкостной фазе равна концентрации в конце процесса в паровой фазе.

2) С отводом пара.

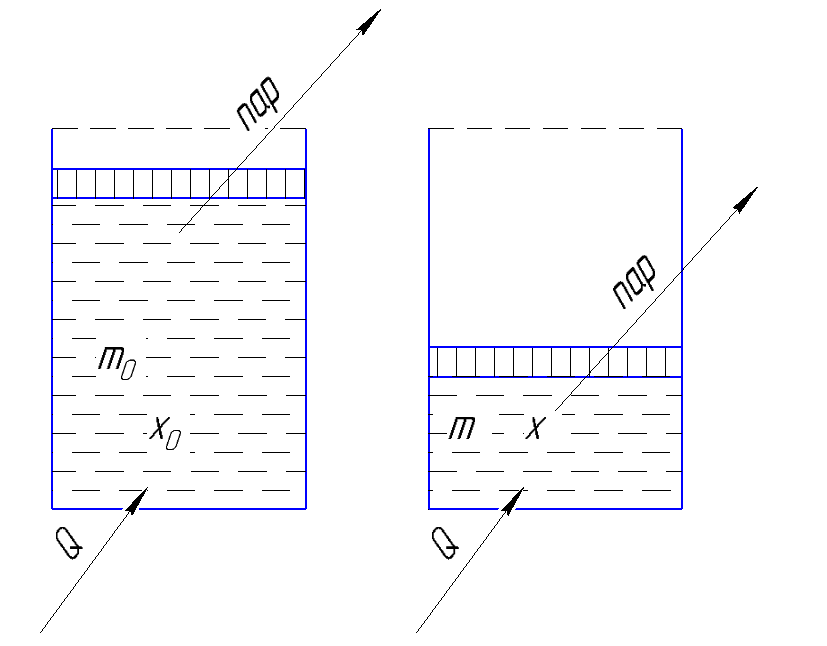
Рисунок 186. Испарение бинарного раствора с отводом пара.

В исходном состоянии жидкость имела массу М₀, и х₀ – начальная концентрация низкокипящего компонента. В результате через 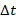ушло в пар dM, масса стала М, концентрация х.

Запишем уравнение закона сохранения массы для процесса испарения по низкокипящему компоненту.

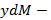ушло в пар низкокипящего компонента;

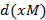– из жидкости ушло низкокипящего компонента.

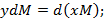
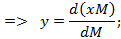
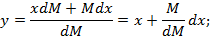
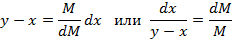
Считаем процесс испарения равновесным, т.е. для данной температуры и давления концентрация низкокипящего компонента в паровой фазе равна равновесной концентрации, которая зависит от концентрации низкокипящего компонента в жидкости.

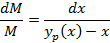
Поскольку 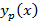имеет существенно нелинейный характер, то решить данное дифференциальное уравнение можно только численными методами

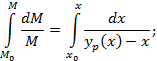
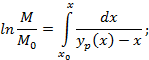
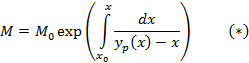
Рассмотрим данный процесс испарения в координатах (Т-х).

При использовании этого метода испарения жидкости выводится низкокипящий компонент и она обогащается высококипящим. Таким образом осуществляя кипение с непрерывным отводом пара можно получить сколь угодно чистую жидкость, состоящую преимущественно из высококипящего компонента.

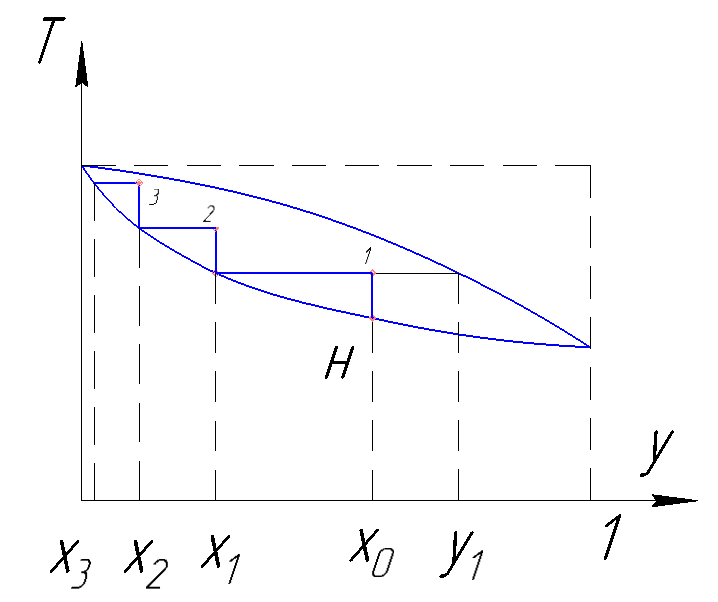
Рисунок 187. Испарение бинарного раствора с отводом пара.

Для определения количества оставшейся жидкости в зависимости от концентрации низкокипящего компонента в жидкости традиционно используют графическое численное решение на диаграмме (y-x) :

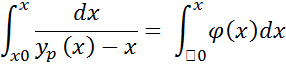
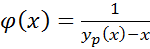
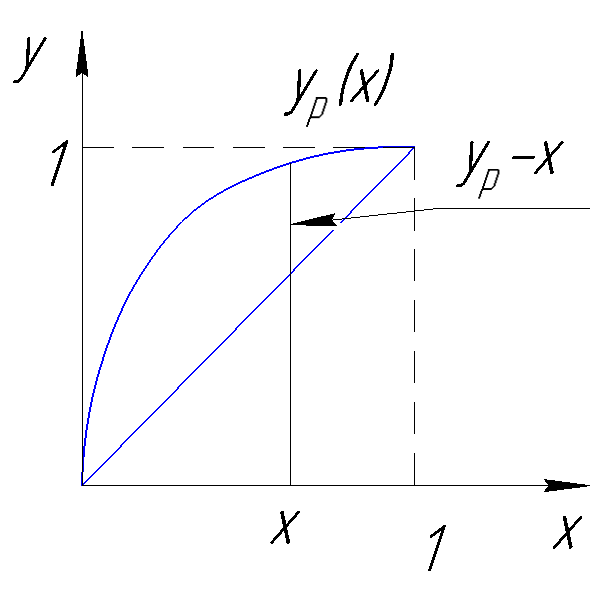
Рисунок 188. Определение количества оставшейся жидкости по y-x диаграмме.

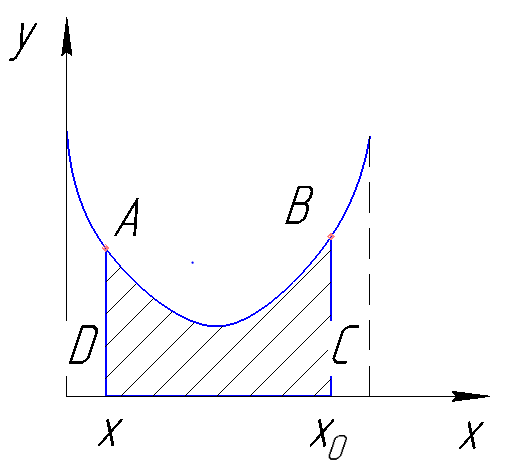
Рисунок 189. Определение количества оставшейся жидкости по y-x диаграмме.

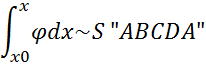
В результате получаем жидкость, обогащенную высококипящим компонентом.

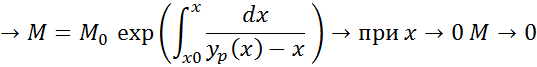
Аналогичный, но обратный процесс будем иметь при конденсации бинарной смеси с непрерывным отводом жидкости . В этом случае пар с течением времени будет обогащаться низкокипящим компонентом.

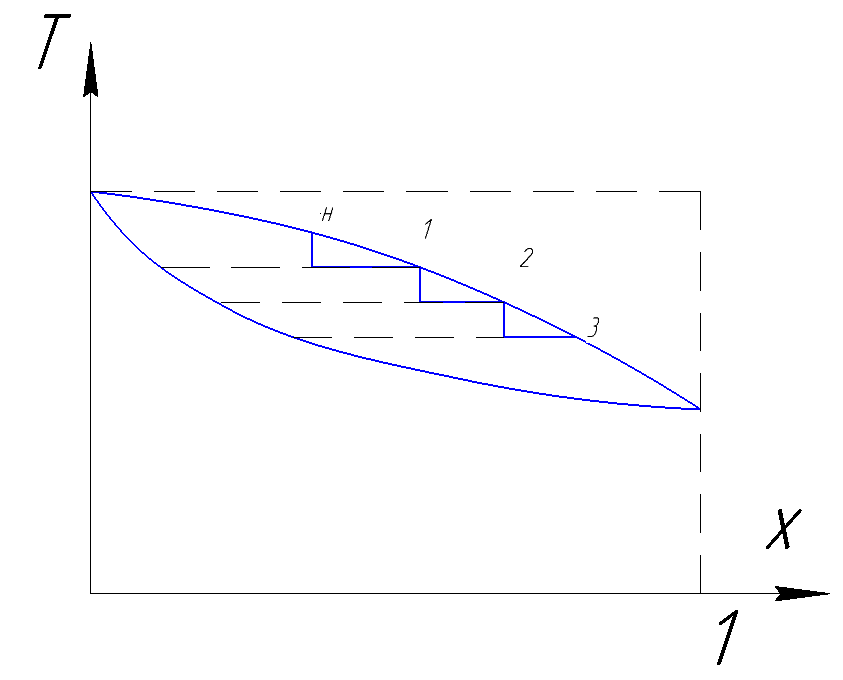
Рисунок 190. Конденсирование с отводом жидкости.