Взаимодействие двух электрически заряженных тел.

Проведём расчёт силы взаимодействия двух электрически заряженных тел объёмами V₁ и V₂, расположенных в пространстве как показано на рис. 6, в символической форме и в форме проекций на направления декартовой системы координат.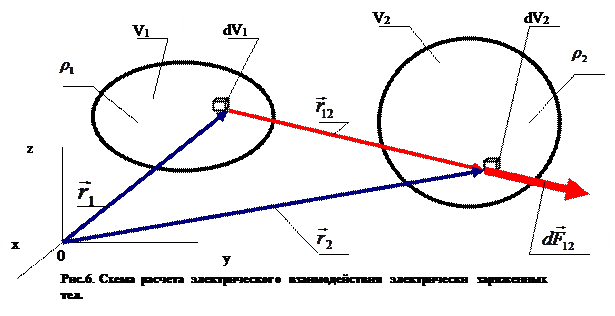

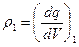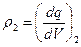Объёмные плотности электрического заряда и являются известными функциями координат декартовой системы координат 0xyz. Выделим в теле 1 элементарный бесконечно малый объём dV₁ и вычислим электрический заряд этого объёма - 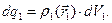Проделаем аналогичную операцию с телом 2: 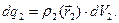Элементарные электрические заряды 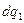и 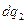можно считать точечными, расстояние между ними определяется длиной вектора 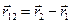, где радиус-векторы 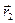и 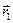описывают положение в пространстве выделенных элементарных объёмов dV₂ и dV₁. Направление элементарной силы 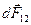, с которой элементарный заряд 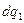действует на элементарный заряд 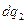определяется направлением вектора 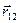, начало которого расположено в месте нахождения первого элементарного заряда, а конец – в месте расположения второго элементарного заряда. 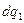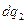Для определённости примем, что заряды и являются одноимёнными. В силу принципа суперпозиции действие первого заряженного тела на второе равно сумме элементарных сил взаимодействия 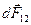. Сложение элементарных сил выполним в два этапа. Сначала определим суммарную силу, с которой тело 1 действует на элементарный заряд dq₂:

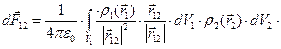. (1)

Теперь просуммируем все элементарные силы, действующие на элементарные заряды тела 2 со стороны тела 1:

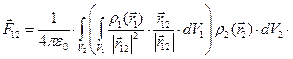(2)

Если составляющие радиус-вектора 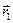суть {x₁, y₁,z₁}, а составляющие радиус-вектора 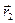- {x₂, y₂,z₂}, то составляющие вектора 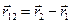имеют вид: 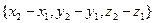, а модуль этого вектора определен выражением 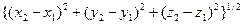. Символическая форма записи результата расчета позволяет практически вычислить проекции вектора 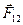на направления координатных осей

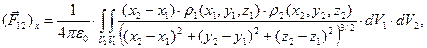
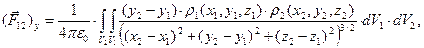(3)

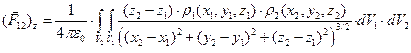
В простейших случаях интегрирование полученных выражений удаётся выполнить аналитически, иногда удаётся свести эти выражения к табулированным специальным функциям математической физики, в общем случае приходится прибегать к использованию численных методов вычисления кратных интегралов. Специальное математическое обеспечение современных персональных компьютеров позволяет это выполнить.

Вывод: силу взаимодействия двух заряженных тел конечных размеров с известными законами распределения электрических зарядов всегда можно рассчитать, возникающие при этом трудности не принципиальные, а вычислительные. Заметим, что в реальных условиях распределение электрических зарядов по объёму или по поверхности тела заранее может быть неизвестно, его определение в этом случае представляет собой отдельную самостоятельную задачу. В этом состоит существенное различие электростатического и гравитационного взаимодействий.