Основные операции с комплексными векторами
Рассмотрим основные операции с комплексными векторами на примере операций с комплексными числами. Заданы два комплексных вектора:
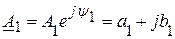
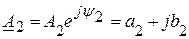 .
.
1. Сумма двух комплексных векторов 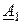 и
и 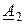 есть также комплексный вектор
есть также комплексный вектор 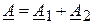 . Для его получения используется алгебраическая форма записи, в которой отдельно складываются действительные и мнимые части комплексного числа.
. Для его получения используется алгебраическая форма записи, в которой отдельно складываются действительные и мнимые части комплексного числа.
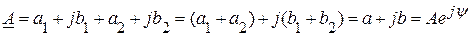 .
.
2. Разность двух комплексных векторов 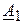 и
и 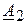 есть также комплексный вектор
есть также комплексный вектор 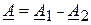 . Нахождение разности двух комплексных векторов, аналогично операции суммирования.
. Нахождение разности двух комплексных векторов, аналогично операции суммирования.
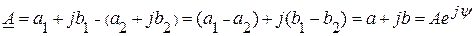 .
.
3. Произведение двух комплексных векторов 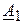 и
и 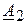 есть также комплексное вектор
есть также комплексное вектор 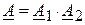 . Для его получения используется показательная форма записи.
. Для его получения используется показательная форма записи.
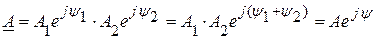 .
.
Выполнение операции умножения можно осуществить с использованием алгебраической формы записи. Для этого необходимо перемножить два комплексных числа по правилу умножения многочленов, при этом следует помнить, что 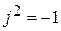 .
.
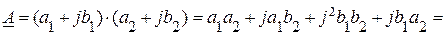
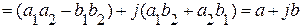 .
.
4. Деление двух комплексных векторов 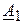 и
и 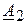 есть также комплексный вектор
есть также комплексный вектор 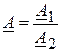 . Для ее получения используется показательная форма записи.
. Для ее получения используется показательная форма записи.
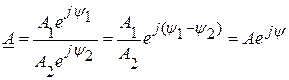 .
.
При выполнении операции деление, можно использовать также алгебраическую форму записи, но при этом следует помнить, что произведение 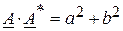 . Тогда операция деление выглядит следующим образом:
. Тогда операция деление выглядит следующим образом:
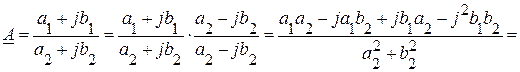
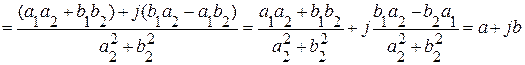 .
.
Операции с комплексными числами проиллюстрируем на конкретных примерах.
Пример 3.8. Допустим, имеем четыре комплексных числа
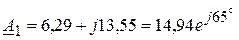 ,
, 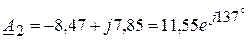 ,
, 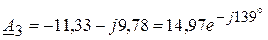 ,
, 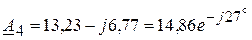 .
.
Дата добавления: 2016-06-22; просмотров: 1916;











