Расчет разветвленных цепей синусоидального тока методом проводимостей
Метод применяется для разветвленных цепей с одним источником питания.
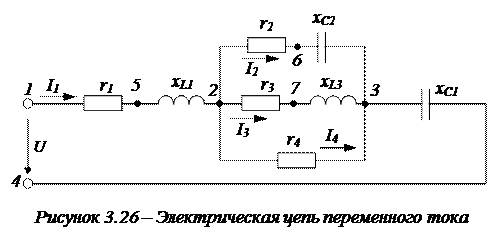
Допустим, имеется схема электрической цепи переменного тока, приведенная на рисунке 3.26.
 |
Рассмотрим основные этапы расчета.
1. Последовательно соединенные элементы в параллельных ветвях (2, 3, 4)преобразуем в эквивалентные параллельные. В результате схема будет иметь вид, представленный на рисунке 3.27.
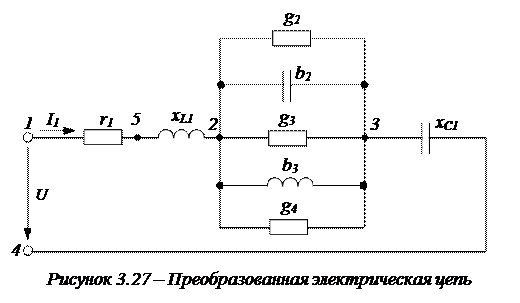 |
Проводимости каждой ветви соответственно равны:
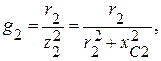
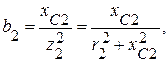
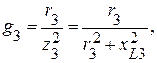
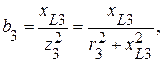
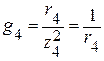 .
.
В результате в параллельных ветвях получились только однородные элементы.
2. Заменим параллельно соединенные активные и реактивные сопротивления эквивалентными. В результате получим схему, приведенную на рисунке 3.28.
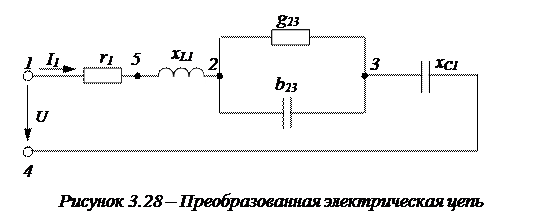 |
Эквивалентные проводимости
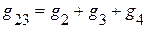 ;
;
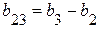 .
.
Предположим, что b2 > b3 тогда элемент b23 имеет емкостной характер (рис. 3.28).
3. Параллельно соединенные проводимости g23 и b23 преобразуем в эквивалентно последовательные r23 и x23, получим схему, представленную на рисунке 3.29.
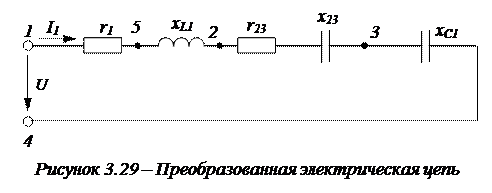 |
Сопротивления преобразованной схемы соответственно равны
 ,
, 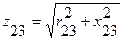 .
.
4. Полученная схема имеет только последовательно соединенные элементы.
Определяем полное сопротивление эквивалентной схемы: 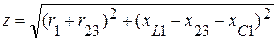 .
.
5. Определяем токи в ветвях.
5.1. Ток 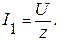
5.2. Определяем токи в параллельных ветвях.
5.2.1. Определяем напряжение 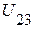 на зажимах параллельной ветви:
на зажимах параллельной ветви: 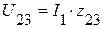 .
.
5.2.2. Токи в параллельных ветвях соответственно равны:
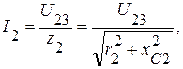
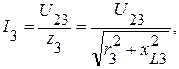
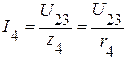 .
.
Пример 3.3. Возможные варианты расчета разветвленных цепей синусоидального тока методом проводимости, рассмотрим на примере электрической цепи, представленной на рисунке 3.30. Заданы величины U23 = 120 (B), r1 = 5 (Ом), r2 = 9 (Ом), r3 = 12 (Ом), r4 = 7 (Ом), хС1 = 12 (Ом), хС2 = 12 (Ом), хL3 = 16 (Ом), хL4 = 24 (Ом). Необходимо определить токи во всех ветвях электрической цепи.
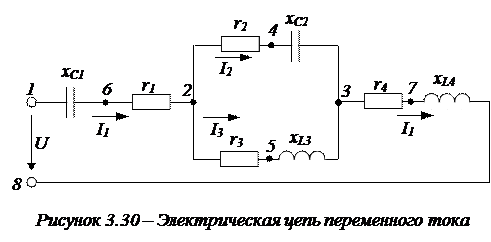 |
1. Последовательно соединенные элементы в параллельных ветвях (2 и 3)преобразуем в эквивалентные параллельные. В результате схема будет иметь вид, представленный на рисунке 3.31.
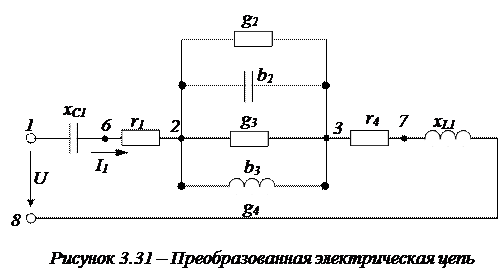 |
Проводимости каждой ветви соответственно равны:
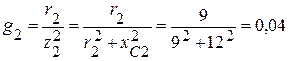 (См),
(См),
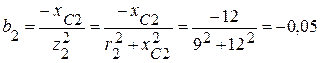 (См),
(См),
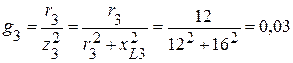 (См),
(См),
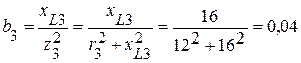 (См).
(См).
В результате в параллельных ветвях получились только однородные элементы.
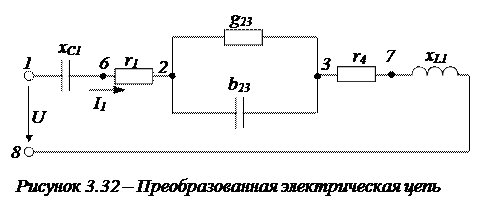 2. Заменим параллельно соединенные активные и реактивные сопротивления эквивалентными. В результате получим схему, приведенную на рисунке 3.32.
2. Заменим параллельно соединенные активные и реактивные сопротивления эквивалентными. В результате получим схему, приведенную на рисунке 3.32.
Эквивалентные проводимости
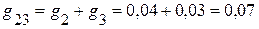 (См),
(См),
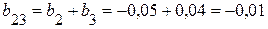 (См).
(См).
Так как b23 < 0, то b 23 - емкостной элемент.
3. Параллельно соединенные проводимости g23 и b23 преобразуем в эквивалентно последовательные r23 и x23, получим схему, представленную на рисунке 3.33.
 |
Сопротивления преобразованной схемы:
активное - 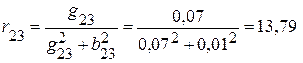 (Ом),
(Ом),
реактивное - 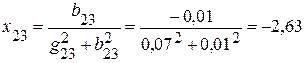 (Ом),
(Ом),
полное - 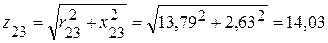 (Ом).
(Ом).
4. Полученная схема имеет только последовательно соединенные элементы, определяем полное сопротивление эквивалентной схемы:
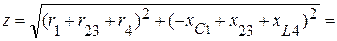
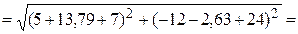
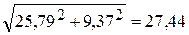 (Ом).
(Ом).
5. Определяем токи в ветвях.
5.1. Токи в параллельных ветвях соответственно равны:
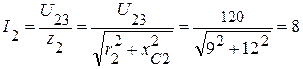 (А),
(А),
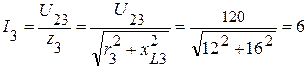 (А).
(А).
5.2. Общий ток 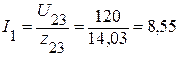 (А).
(А).
6. Определяем напряжение, приложенное к схеме:
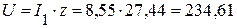 (В).
(В).
Дата добавления: 2016-06-22; просмотров: 2591;











