Сочетания и некоторые свойства сочетаний
Сочетания из n по m m-элементные подмножества n-элементного множества.
Пример: Решим следующую задачу. Пусть в коробке находится пять пронумерованных шаров {1, 2, 3, 4, 5}. Перечислите все способы выбора двух шаров из этих пяти.
Каждому способу выбора двух шаров из пяти соответствует некоторое двухэлементное подмножество пятиэлементного множества. Перечислим эти подмножества:

Обратите внимание, что подмножества (2,1) и (1,2) содержат один и тот же набор элементов и поэтому отождествляются. Итак, у пятиэлементного множества 10 двухэлементных подмножеств.
Рассмотрим все подмножества, состоящего из трех элементов {a, b, c}.
Их восемь:
· Ø – пустое множество, как принадлежащее любому множеству;
· {a}, {b}, {c} – одноэлементные 3 множества;
· {a, b}, {a, c}, {b, c} – двухэлементные 3 множества;
· {a, b, c} – одно множество из трех элементов, то есть полное рассматриваемое множество.
В сумме получили 8 различных подмножеств.
Число подмножеств, m элементов в каждом, содержащихся во множестве из n элементов, обозначается Cnm (читается "це из эн по эм") Буква C выбрана для обозначения числа сочетаний в связи тем, что по-французски слово "сочетание" - "combinaison" - начинается с этой буквы.
C52 = 10
В комбинаторике конечные множества называются сочетаниями.
В сочетаниях нас интересует только сами элементы множества и не интересует их порядок.
Важно, какие конкретно элементы множества входят в каждое соединение.
Число сочетаний, перестановок и размещений связаны по формуле:
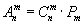
Действительно, чтобы получить все размещения из n элементов по m надо:
1) взять n-элементное множество;
2) выделить m-элементное подмножество. Это можно сделать Cnm - способами. Всего получим Cnmупорядоченных множеств, так как в каждом m – элементном подмножестве возможно установить Рmпорядков, где Рm – число перестановок из m элементов.
| Следовательно, | 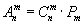
| , а | 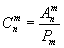
| . |
Подставив сюда уже известные нам выражения
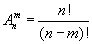 и Рm = m!, m ≤ n и Cn0 = 1, получим
и Рm = m!, m ≤ n и Cn0 = 1, получим
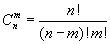
| что можно записать иначе: | 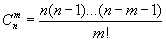
|
Дата добавления: 2020-03-21; просмотров: 668;











