Размещения. Упорядоченные множества
Определение: Множество вместе с заданным порядком расположения его элементов называется упорядоченным множеством. Если в упорядоченном множестве изменить расположение элементов, то мы получим другое, отличное от первого множество.
В комбинаторике конечные упорядоченные множества называются размещениями.
Число размещений из n элементов по m обозначают Anm (читают А из эм по эн).
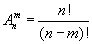
При m = 0 по формуле получаем: An0 = 1.
Это верно: существует только одно пустое множество, оно является подмножеством любого множества.
Заметим еще, что 0! = 1; 1! = 1; и Ann = Рn = n!
Пусть исходное множество состоит из букв (а, в, с). Ставится задача: посчитать количество размещений из трех элементов по два: A32.
Будем составлять упорядоченные двухэлементные подмножества из данных трех элементов а, в, с.
Для наглядности составим таблицу, где и запишем все возможные подмножества.
| а | в | с | |
| а | (а,а) | (а,в) | (а,с) |
| в | (в,а) | (в,в) | (в,с) |
| с | (с,а) | (с,в) | (с,с) |
Размещения с повторениями – каждый элемент, входящий в комбинацию, может быть представлен более чем одним экземпляром (включая элементы диагонали таблицы).
| Число возможных размещений из n различных элементов по m находятся по формуле: | 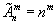
|
В дальнейшем размещения без повторений мы будем называть одним словом – «размещения».
Размещение без повторений – каждый элемент, входящий в комбинацию, представлен единственным экземпляром (исключая элементы диагонали таблицы)
Будем составлять упорядоченные двухэлементные подмножества из данных трех элементов а,в,с. (а,в); (а,с); (в,с); (в,а); (с,а); (с,в).
На первое место можно поставить любой из трех элементов, это можно сделать тремя способами, на второе место – любой из оставшихся элементов, то есть двумя способами, всего получим 3 · 2 соединений,т.е. A32 = 3 · 2 = 6.
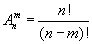
Задача 1: Учащиеся 11-го класса изучают 9 учебных предметов. В расписании учебных занятий на один день можно поставить 4 различных предмета. Сколько существует различных способов составления расписания на один день?
Решение: Имеем 9-элементное множество, элементы которого учебные предметы. При составлении расписания мы будем выбирать 4-элементное подмножество и устанавливать в нем порядок. Число таких способов равно числу размещений из девяти по четыре, то есть A94:
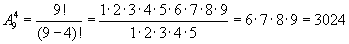
Контрольные вопросы:
· Что такое комбинаторика.
· Правило суммы и произведения?
· Что такое размещение?
· Как вычислить размещение m элементов из n?
· Что такое перестановка?
· Как вычислить число перестановок n предметов?
Дата добавления: 2020-03-21; просмотров: 601;











