УРАВНЕНИЯ СОСТОЯНИЯ РЕАЛЬНЫХ ГАЗОВ

По свойствам реальные газы (пары) значительно отличаются от идеального газа.

Во-первых, реальный газ не сохраняет условий идеальности (имеются силы взаимодействия между молекулами, молекулы обладают конечным объемом и т.п.); во-вторых, реальный газ (пар) – неустойчивое рабочее тело, которое в ходе термодинамического процесса может менять свое агрегатное состояние.

Вместе с тем пары многих жидкостей (воды, аммиака, фреона, щелочных металлов и др.) являются основными видами термодинамических рабочих тел, при помощи которых возможно трансформирование теплоты в механическую работу или обратно в целом ряде теплотехнических установок (паровые турбины, тепловые трубы, холодильные установки, МГД-генераторы).

Уравнение состояния и явления переноса в реальных газах и жидкостях тесно связаны с силами, действующими между молекулами. Молекулярно-статистическая теория, связывающая общие свойства с межмолекулярными силами, сейчас хорошо разработана для разреженных газов и в меньшей степени – для плотных газов и жидкостей. Вместе с тем, измерение макроскопических свойств позволяет в принципе определить закон, по которому действуют силы между молекулами. Более того, если вид взаимодействия определен, то становится возможным получить уравнение состояния или коэффициенты переноса для реальных газов.

Уравнение состояния идеального газа точно только в том случае, когда газ весьма разрежен или его температура сравнительно высока. Однако уже при атмосферных давлении и температуре отклонения от этого закона для реального газа становятся ощутимыми.

По определению идеального газа его молекулы представляют собой материальные точки и объем занимаемый газом равен объему межмолекулярного пространства. Следовательно, при p→∞, υ→0, что хорошо согласуется с понятием идеального газа.

В реальных газах молекулы могут двигаться не во всем объеме сосуда, т.к. часть объема занята самими молекулами и при бесконечно большом давлении объем не может быть бесконечно малым. На первый взгляд кажется, что нужно из занимаемого газом объема сосуда υ просто вычесть сумму объемов всех молекул. Но молекулярная статистика указывает, что для расчета средней длины свободного пути или числа столкновений в секунду какой-нибудь молекулы надо считать диаметр ее увеличенным вдвое, а все остальные молекулы представить в виде точек. Можно сделать и наоборот, считать выбранную молекулу за точку, а диаметр всех остальных молекул увеличить вдвое. Характер движения и результаты подсчёта останутся неизменными, в которых получается, что точечной молекуле осталось для движения пространство, объем которого меньше объема сосуда на величину, в восемь раз большую объема всех молекул, т.к. объем молекулы при удвоении диаметра увеличивается в восемь раз. Однако строго произведенный расчет показывает, что на самом деле уменьшение объема составляет не восьмикратный объем молекул, а всего лишь учетверенный. Впрочем, и это последнее утверждение правильно лишь приблизительно. Обозначим в общем случае эту величину, пропорциональную объему, занимаемому молекулами, через b:

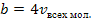
Тогда свободный объем пространства, в котором движутся молекулы, будет равен b−υ (этот объем может изменяться до нуля при p→∞).

Во-вторых, в реальном газе имеются силы взаимодействия между молекулами. При своем движении молекулы реального газа взаимодействуют, в результате чего средняя скорость движения такой молекулы меньше, чем у молекулы идеального газа. Поэтому при одинаковой температуре и сила удара молекулы реального газа о стенки сосуда будет меньше, чем у молекулы идеального газа. Значит, действительное давление реального газа на стенку сосуда p будет меньше, чем давление идеального газа при одной и той же температуре:

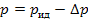
где p – давление на стенку сосуда реального газа;

р_ид – давление на стенку сосуда идеального газа;

Δp – поправка, учитывающая уменьшение давления вследствие наличия сил взаимодействия между молекулами.

Для реального газа действительное давление газа на стенку равно

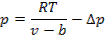
Согласно второму закону Ньютона величина сил взаимодействия между молекулами будет прямо пропорциональна массе частиц. Поэтому, если взять два соседних слоя газа, силы взаимодействия между ними будут прямо пропорциональны плотности газа в этих слоях:

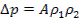
Считая, что плотности отдельных слоев газа одни и те же получим

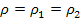
и 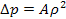, но т.к. 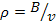следовательно,

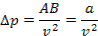
Тогда

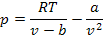
Откуда получаем уравнение Ван-дер-Ваальса для реального газа:

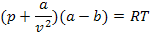
Раскрывая скобки, получим уравнение третьей степени относительно v:

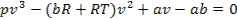
При решении этого уравнения могут быть три случая: 1) один корень действительный и два мнимые; 2) три корня действительные и равные между собой; 3) три корня действительные и различные по величине.

В последнем случае на первый взгляд получается странное явление: тело при определенных температуре и давлении может иметь три разных объема. Впервые объяснение этому явлению дал Менделеев, а английский ученый Эндрюс своими опытами над углекислым газом подтвердил положения Менделеева. Эндрюс сжимал углекислый газ при постоянной температуре. При различных опытах бралась различная температура. Результаты исследования наносились на диаграмму pυ

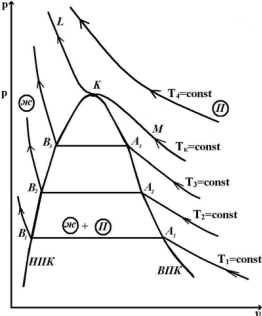
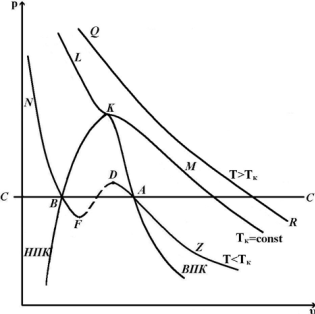
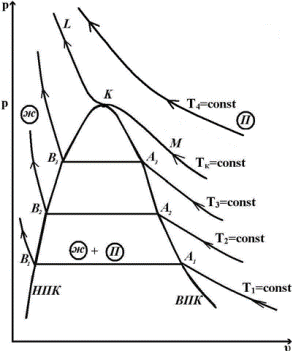
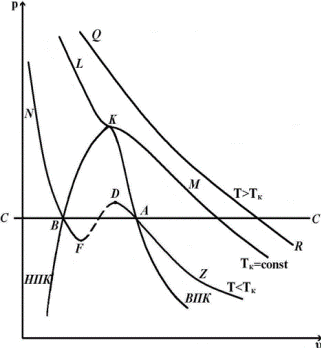
Наблюдения показали, что линия LKM – изотерма, имеющая перегиб в точке К, причем при температурах T>Tк получаются гиперболы, а при температурах T<Tк на изотермах получаются горизонтальные участки Эти участки, как показал опыт, соответствуют превращению газа в жидкость. В точках A₁A₂A₃ конденсация газа начинается, а в точках B₁B₂B₃ заканчивается. Соединив точки одинакового агрегатного состояния, мы получим кривые КA₁ и КВ₁ сходящиеся в точке К.

Линия КA₁ называется верхней пограничной кривой (ВПК).

Линия КВ₁ - нижней пограничной кривой (НПК).

Точка К, где горизонтальный участок отсутствует, называется критической точкой. Изотерма, проходящая через критическую точку, называется критической; давление, удельный объем и температура в точке К называются также критическими и обозначаются соответственно p_кр, υ_кр, Т_кр. Критическая изотерма не имеет горизонтального участка, а лишь точку перегиба.

Анализируя расположение ВПК и НПК, отметим три области агрегатного состояния. Область, расположенная левее НПК и ниже критической изотермы, соответствует жидкому состоянию вещества, область, расположенная вправо от ВПК, соответствует газообразному состоянию вещества (перегретый пар – реальный газ). Область, расположенная между ВПК и НПК, соответствует смеси газа и жидкости.

Итак, если при решении уравнения (***) оказывается, что три корня действительные и разные, то это означает, что при некотором значении p и Т вещество имеет три значения удельного объема υ, соответствующих трем состояниям вещества - газообразному, жидкому и промежуточному (смеси газа и жидкости), наибольший корень соответствует газообразному (т. А), а наименьший - жидкому состоянию (т. В) (рис. 9.2). Этот случай наблюдается при сравнительно низких температурах, которым соответствуют изотермы вида NBFEDAZ, имеющие с горизонталью CC три точки пересечения BEA. Если все три корня действительные и равные друг другу, то это условие будет соответствовать критической точке K на кривой LKM. Если два корня будут мнимые, а один действительный, то это будет соответствовать газообразному состоянию.

Поэтому можно сказать, что уравнение Ван-дер-Ваальса охватывает не только газообразную, но и жидкую фазу. Это уравнение может быть названо уравнением состояния. Следует отметить, что переход из газообразного состояния в жидкое не всегда происходит по прямой (например, AB). Можно создать такие условия, при которых начало конденсации будет запаздывать и дальнейшее сжатие будет сопровождаться повышением давления по кривой AD. В этих состояниях пар называется переохлажденным, итак

AD - переохлажденный пар,

BF - перегретая жидкость.

Участки AD и BF малоустойчивы, однако могут быть реально получены. Участок DEF соответствует состояниям совершенно неустойчивым и физически неосуществимым. Для этого участка .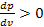

AB дает линию устойчивого протекания процесса конденсации. Кривая ZADEFBN удовлетворяет уравнению Ван-дер-Ваальса. Если сжимать газ при T>Tкр, то конденсации газа быть не может.

Уравнение Ван-дер-Ваальса является лишь грубым приближением, т.к. экспериментально обнаружено, что объем υ_ж в жидкой фазе значительно меньше, чем значение b, полученное из результатов по определению зависимости p от υ и Т в газе.

Однако уравнение Ван-дер-Ваальса может быть использовано как уравнение состояния для многих газов в сравнительно небольших интервалах температур.

Для более широкого диапазона изменения переменных, кроме уравнения Ван-дер-Ваальса, имеется и ряд других уравнений состояния, полученных как теоретически, так и на основании экспериментов (уравнения Бертло, Дитеричи, Битти – Бриджмена, Вукаловича – Новикова и др.) Некоторые из этих уравнений достаточно точны лишь в узкой области значений температуры и плотности, другие применимы к описанию как газообразной, так и жидкой фазы. Кроме того, уравнение состояния реального газа может быть описано в очень широком интервале температуры и давления с помощью соотношения степенного ряда:

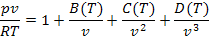
Это уравнение называется вириальным уравнением состояния. Зависящие от температуры функции В(Т), С(Т) и т.д. выступают здесь как второй, третий и т.д. вириальные коэффициенты.

Вириальные коэффициенты по своему существу определяют отклонения реальных газов от идеальных через свойства межмолекулярных сил.