Сущность второго закона ТД
Iый закон ТД дает необходимые сведения для составления энергетического баланса в ТД процессах и тепловых машинах. Однако он ничего не говорит о возможности осуществления таких процессов и циклов реальных машин.
IIой закон ТД, так же как первый, является экспериментальным. Он показывает направления протекания и пределы осуществимости реальных, следовательно необратимых, процессов. Этот закон имеет много проявлений и соответственно много формулировок.
Формулировка Больцмана.
Свойство природы – стремиться от состояний менее вероятных к состояниям более вероятным. Наиболее вероятным состоянием ТДС является состояние термодинамического равновесия, при котором внутри нее отсутствуют макроскопические потоки вещества и энергии. Если изолированную систему вывести из состояния ТД равновесия, например, создав разницу температур между ее отдельными частями, то за счет самопроизвольных естественных процессов теплообмена она придет к состоянию равновесия, при котором температура всех тел системы выравнивается, и будет находиться в этом состоянии бесконечно долго, пока не начнется взаимодействие с ОС.
Формулировка Клаузиуса.
Теплота самопроизвольно может переходить от тел с большей к телам с меньшей температурой и не может сама собой, даровым способом, переходить от тел с меньшей к телам с большей температурой.
Оствальд отметил невозможность создания вечного двигателя второго рода, в котором вся подведенная теплота превращается в работу.
Математическое выражение IIго закона ТД.
Термический КПД цикла Карно с одной стороны равен
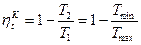 ,
,
с другой стороны как для любых тепловых машин равен
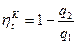 , Þ
, Þ
Þ 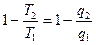 ; Þ
; Þ 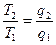 ; Þ
; Þ 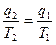
или учитывая знак 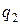 (считая подведенную теплоту
(считая подведенную теплоту 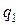 величиной положительной, а отведенную
величиной положительной, а отведенную 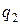 отрицательной)
отрицательной)
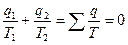
– для обратимого цикла Карно
где
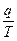 - приведенная теплота.
- приведенная теплота.
Любой обратимый цикл можно разбить адиабатами на бесконечное множество элементарных циклов, состоящих из двух адиабат и двух малых отрезков кривой, ограничивающей цикл. Изменение температуры по отрезкам кривой мало, следовательно в каждом элементарном цикле можно отрезки кривой заменить на изотермы и таким образом исследуемый цикл будет представлять собой большое количество циклов Карно.
Для цикла 1-2-3-4-1
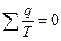 ;
;
для всего количества циклов
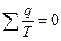 ;
;
при бесконечном количестве адиабат
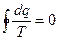
- интеграл Клаузиуса.
Для произвольного обратимого процесса
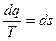
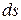 - изменение энтропии (функции состояния).
- изменение энтропии (функции состояния).
КПД необратимого цикла Карно всегда меньше КПД обратимого, и тогда
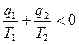 ;
; 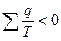
для произвольного необратимого цикла
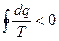
для произвольного необратимого процесса
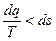 ;
; 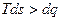 .
.
В итоге для цикла Карно- 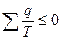 ,
,
для произвольного цикла- 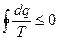 ,
,
для произвольного процесса- 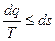 или
или 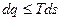 .
.
Для адиабатной системы 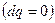 , второй закон термодинамики запишется в виде
, второй закон термодинамики запишется в виде
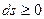
Если в адиабатной системе протекают естественные самопроизвольные процессы, то такая система стремится к состоянию термодинамического равновесия, т.е. энтропия возрастает 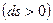 . Когда наступает термодинамическое равновесие
. Когда наступает термодинамическое равновесие 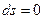 , а
, а 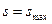
Т.о. IIй закон термодинамики называют законом возрастания энтропии.
Объединяя Iй и IIй законы термодинамики можно сказать: «энергия изолированной системы постоянна, а ее энтропия увеличивается».
6.2 Объединенные уравнения Iго и IIго законов термодинамики для простых систем. Условие термодинамического равновесия
Для произвольного процесса, как было показано ранее, можно записать
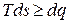 ,
,
а согласно Iму закону термодинамики
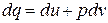 .
.
Подставляя одно в другое получим
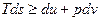
или
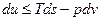
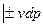
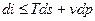
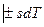
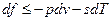
или
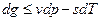
Полученные уравнения и есть объединенные уравнения двух законов термодинамики для простых систем, они позволяют получить условие стремления к равновесию не только для адиабатных систем 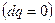 , но и для других условий взаимодействия с окружающей средой.
, но и для других условий взаимодействия с окружающей средой.
1) при 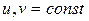
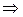
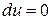 и
и 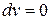 – полная изоляция системы.
– полная изоляция системы.
Из уравнения (1), следует что 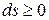
(Знаки: 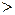 – для неравновесных процессов;
– для неравновесных процессов; 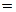 – для равновесных процессов.)
– для равновесных процессов.)
при неравновесных процессах 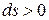 , при достижении термодинамического равновесия
, при достижении термодинамического равновесия 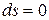 ,
, 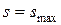 , т.е. если в изолированной системе протекают неравновесные процессы, то система стремится к равновесию.
, т.е. если в изолированной системе протекают неравновесные процессы, то система стремится к равновесию.
2) при 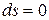 и
и 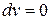 – изохорно-изоэнтропная система, т.е. система не обменивается с окружающей средой работой, но может обмениваться теплотой в таком количестве, чтобы энтропия оставалась постоянной.
– изохорно-изоэнтропная система, т.е. система не обменивается с окружающей средой работой, но может обмениваться теплотой в таком количестве, чтобы энтропия оставалась постоянной.
Из (2) уравнения следует, что 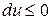 , т.е. при протекании неравновесных процессов внутренняя энергия уменьшается
, т.е. при протекании неравновесных процессов внутренняя энергия уменьшается 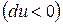 и при достижении термодинамического равновесия
и при достижении термодинамического равновесия 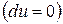 , а внутренняя энергия достигает своего минимального значения
, а внутренняя энергия достигает своего минимального значения 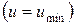 .
.
3) при 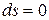 и
и 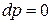 – изобарно-изоэнтропная система.
– изобарно-изоэнтропная система.
Из (3) уравнения следует, что 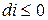 , т.е. при протекании неравновесных процессов энтальпия уменьшается
, т.е. при протекании неравновесных процессов энтальпия уменьшается 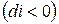 и при достижении термодинамического равновесия
и при достижении термодинамического равновесия 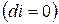 , а энтальпия достигает своего минимального значения
, а энтальпия достигает своего минимального значения 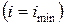 .
.
4) при 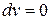 и
и 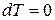 – изохорно-изотермическая система.
– изохорно-изотермическая система.
Из (4) уравнения следует, что 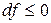 , т.е. при протекании неравновесных процессов свободная энергия уменьшается
, т.е. при протекании неравновесных процессов свободная энергия уменьшается 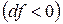 и при достижении термодинамического равновесия
и при достижении термодинамического равновесия 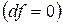 , а свободная энергия достигает своего минимального значения
, а свободная энергия достигает своего минимального значения 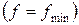 .
.
5) при 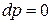 и
и 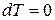 – изобарно-изотермическая система.
– изобарно-изотермическая система.
Из (5) уравнения следует, что 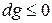 , т.е. при протекании неравновесных процессов свободная энтальпия уменьшается
, т.е. при протекании неравновесных процессов свободная энтальпия уменьшается 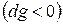 и при достижении термодинамического равновесия
и при достижении термодинамического равновесия 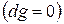 , а свободная энтальпия достигает своего минимального значения
, а свободная энтальпия достигает своего минимального значения 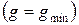 .
.
Таким образом, для не изолированных систем, в зависимости от условий взаимодействия с окружающей средой, протекание в них неравновесных процессов происходит таким образом, в таком направлении, что соответствующая функция состояния системы уменьшается, система стремится к равновесию и при достижении его эта функция состояния достигает своего минимального значения.
Поэтому IIй закон термодинамики это не только закон возрастания энтропии, но и закон уменьшения соответствующей функции состояния.
Объединенные уравнения Iго и IIго законов термодинамики для сложных систем
Термодинамический метод исследования применим и к сложным системам, состоящих из рабочих тел различного химического состава, находящихся в различных агрегатных состояниях. В системе могут протекать химические реакции и осуществляться фазовые переходы.
Компонентой сложной термодинамической системы называют – любое независимое, химически различное вещество, содержание которого не зависит от других компонентов.
Фазами называют различные формы одного и того же вещества, отличающиеся физическими свойствами и разделенные видимыми макроскопическими границами.
Гомогенной ТДС называется такая система, химический состав и физические свойства которой во всех ее частях одинаковы или изменяются непрерывно (без скачков) от одной точки системы к другой.
Гетерогенной – называют систему, состоящую из одной или нескольких компонент, находящихся в различных фазах. (Каждая фаза отделена друг от друга поверхностью раздела, при переходе через которую скачкообразно изменяется химический состав или физические свойства.
И гомогенная и гетерогенная система могут состоять из химически активных компонент.
Характерным признаком сложной ТДС является перераспределение количества вещества между компонентами и фазами, в результате протекания химических реакций и осуществления фазовых переходов, т.е. масса или количество вещества играет роль координаты состояния в таких процессах. Если сложную ТДС вывести из равновесного состояния, то перераспределение массы может происходить и в полностью изолированной системе.
Гиббс ввел в ТД понятие химического потенциала и показал, что причину химических реакций и фазовых переходов следует искать в неоднородностях полей химического потенциала:
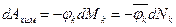
где
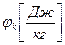 ,
, 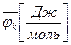 – химический потенциал массовый или мольный;
– химический потенциал массовый или мольный;
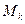 – масса
– масса 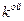 компоненты;
компоненты;
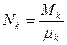 – число молей
– число молей 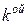 компоненты.
компоненты.
Химические реакции и фазовые переходы изначально не равновесны, так как переход массы не может быть бесконечно малым.
Рассмотрим сложную ТДС, состоящую из 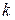 компонент, которая обменивается с окружающей средой теплотой и работой равновесно. Тогда изменение внутренней энергии в целом определится Iм законом ТД.
компонент, которая обменивается с окружающей средой теплотой и работой равновесно. Тогда изменение внутренней энергии в целом определится Iм законом ТД.
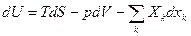
Если вся система обменивается теплотой и работой равновесно, то и каждая компонента обменивается теплотой и работой равновесно.
Тогда для отдельной компоненты можно записать
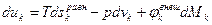
где
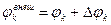
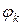 – собственный потенциал компоненты,
– собственный потенциал компоненты, 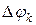 – разность потенциалов между данной компонентой и компонентами всей системы,
– разность потенциалов между данной компонентой и компонентами всей системы,
тогда
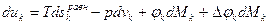 .
.
Дополнительное слагаемое 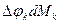 вызвано неравновесностью процесса перераспределения массы, представляет собой некомпенсированную часть взаимодействия, оно всегда положительное. (Опыт показывает, что это потери).
вызвано неравновесностью процесса перераспределения массы, представляет собой некомпенсированную часть взаимодействия, оно всегда положительное. (Опыт показывает, что это потери).
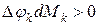
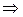 если
если 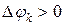 , то имеет место приток массы
, то имеет место приток массы 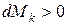 ;
;
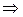 если
если 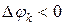 , то имеет место отток массы
, то имеет место отток массы 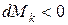 ;
;
Суммирование аналогичных уравнений для всех компонент дает следующее уравнение
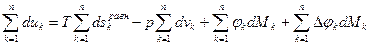
при равновесном обмене теплотой и работой, т.е. 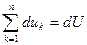
можно записать, что
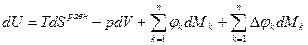 .
.
Опыты показывают, что единственная форма энергии, в которую превращается некомпенсированная часть взаимодействия подсистемы 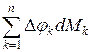 – это теплота, т.е.
– это теплота, т.е. 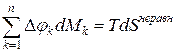 .
.
Тогда
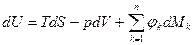
где
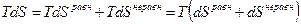
– полное изменение энтропии системы с учетом обратимых и необратимых процессов.
Уравнение (1) – является сводным уравнением Iго и IIго законов ТД для сложных ТДС. Оно показывает, что внутренняя энергия сложной системы может изменяться за счет обмена энергии с ОС в виде теплоты, работы и за счет химических реакций и фазовых переходов.
Совместное уравнение Iго и IIго законов ТД можно записать, используя функции состояния – энтальпию 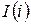 , свободную энергию
, свободную энергию 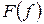 и свободную энтальпию
и свободную энтальпию 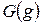 .
.
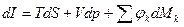
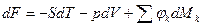
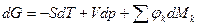
Уравнения (1) и (2)-(4) – условия термодинамического равновесия сложных систем, при различных условиях взаимодействия с ОС, могут быть представлены в виде:
1) при 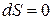 и
и 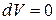 – изохорно-изоэнтропная система.
– изохорно-изоэнтропная система.
Из (1) уравнения следует, что
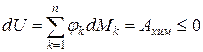 ;
;
2) при 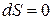 и
и 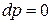 – изобарно-изоэнтропная система.
– изобарно-изоэнтропная система.
Из (2) уравнения следует, что
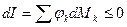 ;
;
3) при 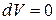 и
и 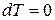 – изохорно-изотермическая система.
– изохорно-изотермическая система.
Из (3) уравнения следует, что
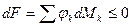 ;
;
4) при 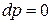 и
и 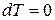 – изобарно-изотермическая система.
– изобарно-изотермическая система.
Из (4) уравнения следует, что
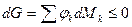 .
.
Эти выражения показывают, что химические реакции и фазовые переходы возможны внутри ТДС только при уменьшении соответствующей функции состояния, при этом в состоянии равновесия функция состояния достигает своего минимального значения.
Дата добавления: 2020-03-21; просмотров: 1069;











