Прогнозирование на основе методов прогнозной экстраполяции
Сущность методов прогнозной экстраполяции состоит в анализе изменений объектов исследования во времени и распространение выявленных закономерностей на будущее.
Термин «экстраполяция» имеет несколько толкований. В широком смысле слова экстраполяция – это метод научного исследования, заключающийся в распространении выводов, полученных из наблюдения над одной частью явления, на другую его часть. В узком смысле слова экстраполяция – это нахождение по ряду данных функции других её значений, находящихся вне этого ряда. Экстраполяция заключается в изучении сложившихся в прошлом и настоящем устойчивых тенденций экономического развития и перенесении их на будущее.
В прогнозировании экстраполяция (экстраполирование) применяется при изучении временных рядов и представляет собой нахождение значений функции за пределами области её определения с использованием информации о поведении данной функции в некоторых точках, принадлежащих области её определения.
Временной ряд представляет собой совокупность последовательных измерений показателя (объём валовой продукции, объём валовых инвестиций, численность занятых в экономике и др.) произведённых через одинаковые интервалы времени. Анализ временных рядов позволяет решать следующие задачи:
исследовать структуру временного ряда, включающую, как правило, тренд – закономерные изменения среднего уровня, а также случайные периодические колебания;
исследовать причинно-следственные взаимосвязи между процессами, проявляющиеся в виде корреляционных связей между временными рядами;
построить математическую модель процесса, представленного временным рядом;
преобразовать временной ряд средствами сглаживания и фильтрации.
Анализ тренда предназначен для исследования изменений среднего значения временного ряда с построением математической модели тренда и с прогнозированием на этой основе будущих значений ряда. Анализ тренда выполняется на основе методов прогнозной экстраполяции, регрессионных моделей и производственных функций. Далее мы подробно рассмотрим каждый из этих методов.
В практической работе временные ряды прогнозируемых показателей приближают следующими элементарными функциями:
У=а0+а1Х (уравнение прямой линии);
У=а0+а1Х+ а2Х2 (парабола второго порядка);
У=а0+а1Х+а2Х2+а3Х3 (парабола третьего порядка);
У=а0+а1lnX (логарифмическая);
У=а0Ха1 (степенная);
У=а0+а1х (показательная).
Различают перспективную и ретроспективную экстраполяцию. Перспективная экстраполяцияпредполагает продолжение уровней ряда динамики на будущее на основе выявленной закономерности изменения уровней в изучаемом отрезке времени. Ретроспективная экстраполяция характеризуется продолжением уровней ряда динамики в прошлое.
Понятием, противоположным экстраполяции, является интерполяция, интерполирование, которое предусматривает нахождение промежуточных значений функции в области её определения.
При экстраполяции предполагается, что:
· текущий период изменения показателей может быть охарактеризован траекторией – трендом;
· основные условия, определяющие технико-экономические показатели в текущем периоде, не претерпят существенных изменений в будущем, т.е. в будущем они будут изменяться по тем же законам, что и в прошлом, и настоящем;
· отклонения фактических значений показателей от линии тренда носят случайный характер и распределяются по нормальному закону.
Сущность метода наименьших квадратовсостоит в минимизации суммы квадратических отклонений между наблюдаемыми и расчётными величинами. Считается, что этот метод лучше других соответствует идее усреднения как единичного влияния учтенных факторов, так и общего влияния неучтенных.
Рассмотрим случай линейной зависимости между переменными Y и Х. Линейная зависимость имеет вид: Yt = a0 +a1Xt. Необходимо определить числовые параметры (а0 и а1), которые наилучшим образом, описали бы зависимость, полученную при наблюдении. Наилучшее согласование достигается в случае, когда сумма квадратов отклонений опытных точек от точек, рассчитанных по теоретической кривой, обращается в минимум:
S = 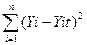 = min.
= min.
Так как, по условию, Yt = a0 +a1Xt, то
S = 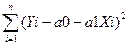 = min
= min
Функция S – функция двух независимых переменных а0 и а1. Для определения экстремума функции нескольких переменных необходимо обращение в ноль её частных производных первого порядка. Далее необходимо сократить все члены уравнений на 2 и сгруппировать члены, содержащие а0 и а1, тогда получим:
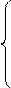 na0 + a1
na0 + a1 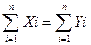
a0 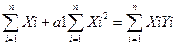 .
.
Теперь для определения а0 и а1 необходимо решить систему уравнений с двумя неизвестными.
Пример. Описать линейную зависимость между объёмом валового регионального продукта (ВРП) Y и численностью работающих в регионе X (таблица 3.1) и составить прогноз ВРП при условии, что численность работающих увеличится на 20% по сравнению с последним наблюдением.
Таблица 3.1 – Динамика ВРП и численности занятых в регионе (данные условные)
| 1-й год | 2-й год | 3-й год | 4-й год | |
| Xi тыс. чел | ||||
| Yi млн руб. |
Решение: при n=4 имеем
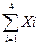 = 10+30+50+70=160
= 10+30+50+70=160 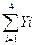 = 11+13+16+18=58
= 11+13+16+18=58
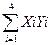 =2 560
=2 560 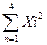 = 8 400
= 8 400
Получим систему уравнений:
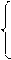 |
 4а0 + 160а1 =58
4а0 + 160а1 =58
160а0 +8 400а1=2 560.
Решением системы уравнений является: а0=9,7 и а1=0,12.
Тогда зависимость имеет вид: Yt=9,7 +0,12Xt.
Для расчёта ошибки прогноза определим отклонение фактических значений Y от расчётных.
Результаты представим в виде таблицы:
| Год | 1-й | 2-й | 3-й | 4-й |
| Yфактическое | ||||
| Yрасчётное | 10,9 | 13,3 | 15,7 | 18,1 |
| Yр -Yф | -0,1 | 0,3 | -0,3 | 0,1 |
Тогда ошибка прогноза равна:
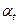 =
= 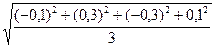 = 0,26.
= 0,26.
При условии, что численность работающих в регионе увеличится на 20%, тогда Yt = 9,7 + 0,12*84=19,78 млн руб.
Вывод: При увеличении численности занятых в регионе на 20% по сравнению с последним наблюдением объём валового регионального продукта составит 19,78 млн руб., т. е. увеличится на 9,8%, при сохранении тенденций развития может иметь отклонение 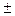 0,26.
0,26.
Метод наименьших квадратов широко применяется в прогнозировании в силу простоты и возможности реализации на ЭВМ. Недостаток данного метода состоит в том, что модель тренда жёстко фиксируется, а это делает возможным его применение только при небольших периодах упреждения, т.е. при краткосрочном прогнозировании.
Метод скользящей средней применяется в том случае, когда ряды динамики характеризуются резкими колебаниями показателей по годам. Такие ряды, как правило, имеют слабую связь со временем и не обнаруживают чёткой тенденции изменения. Наиболее распространенным и простым путём выявления тенденции развития является сглаживание или выравнивание динамического ряда.
Суть различных приёмов, с помощью которых осуществляется сглаживание или выравнивание, сводится к замене фактических уровней динамического ряда расчётными, имеющими меньшую колеблемость, чем исходные данные.
Один из наиболее простых приёмов сглаживания заключается в расчёте скользящих средних, их применение позволяет сгладить периодические и случайные колебания и тем самым выявить имеющуюся тенденцию в развитии.
Метод скользящих средних позволяет отвлечься от случайных колебаний временного ряда, что достигается путём замены значений внутри выбранного интервала средней арифметической величиной. Интервал, величина которого остаётся постоянной, постепенно сдвигается на одно наблюдение. Величина интервала скольжения Р может принимать любое значение от минимального (Р=2) до максимального (Р= N-1, где N – длина рассматриваемого временного ряда). Сглаженный ряд короче первоначального на Р-1 наблюдение.
При использовании метода скользящих средних, прежде всего, определяют величину интервала скольжения, обеспечивающую взаимное погашение случайных отклонений во временном ряду. Если наблюдается определённая цикличность изменения показателей, интервал скольжения должен быть равен продолжительности цикла. При отсутствии цикличности в изменении показателей рекомендуется производить многовариантный расчёт при изменяющемся параметре сглаживания. Лучший вариант Р определяется на основании последующей оценки выровненных рядов (по коэффициентам, темпам роста и т.д.). Найденный таким образом параметр скольжения затем используется для прогнозирования социально-экономических процессов.
Для любого интервала скользящая средняя исчисляется по формуле
Yk = 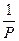
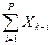 ,
,
где Xk-i – реальное значение показателя в момент времени tk-i;
Р – интервал скольжения;
Yk –значение скользящей средней для момента времени tk.
Пример: Имеется временной ряд показателя ВРП в сопоставимых ценах за 7 лет. (таблица 3.2) Используя метод скользящей средней, сделать прогноз ВРП на последующий 8 год, при Р=3.
Таблица 3.2 – Динамика ВРП (в сопоставимых ценах)
| 1-й год | 2-й год | 3-й год | 4-й год | 5-й год | 6-й год | 7-й год | |
| ВРП, млн руб. |
Рассмотрим решение задачи средствами Excel.
1. Заносим статистические данные на лист Excel.
2. В меню ФАЙЛ выбрать ПАРАМЕТРЫ. Далее выбрать НАДСТРОЙКИ и установить ПАКЕТ АНАЛИЗА.
3. ДАННЫЕ выберите команду АНАЛИЗ ДАННЫХ.
В открывшемся диалоговом окне АНАЛИЗ ДАННЫХ выберите инструмент СКОЛЬЗЯЩЕЕ СРЕДНЕЕ Þ ОК.
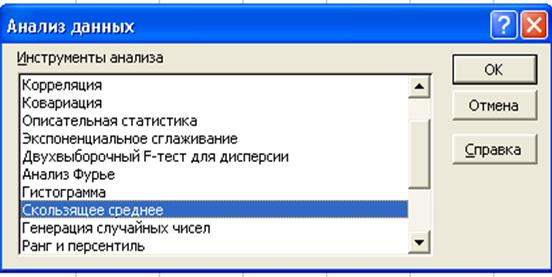
4. В диалоговом окне СКОЛЬЗЯЩЕЕ СРЕДНЕЕ необходимо определить следующие параметры:
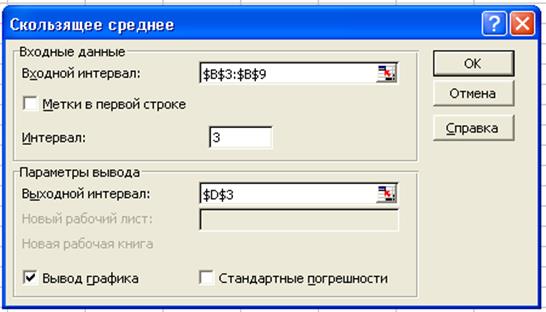
· В поле Входной интервал укажем диапазон с исходными данными (В3:В9).
· Укажем Интервал скольжения равный 3 (минимальное значение равно 2).
· Установим курсор в поле Выходной интервал, мышкой укажем любую ячейку, например С14.
· Установим флажок на команде вывод графика.
· После того как все параметры заданы, щёлкнем по кнопке ОК, Excel выполнит все необходимые вычисления и разместит результаты на листе.
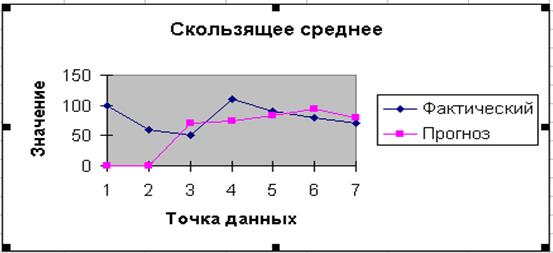
5. Правой кнопкой мыши нажмите на одно из значений графика Прогноза. Далее в диалоговом окне выберите Добавить линию тренда.
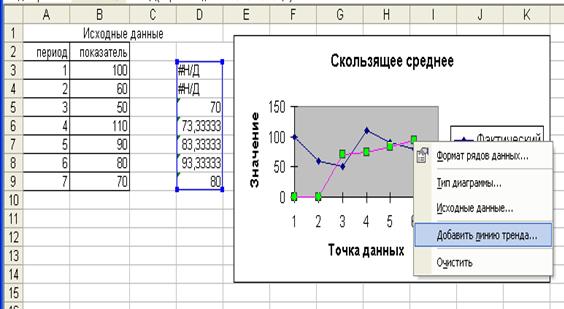
6. В диалоговом окне Линия тренда выберите тип предполагаемой зависимости, например, предположим, что зависимость линейная. Далее выберите команду Параметры, в появившемся диалоговом окне отметьте флажок на команде Показать уравнение на диаграмме.
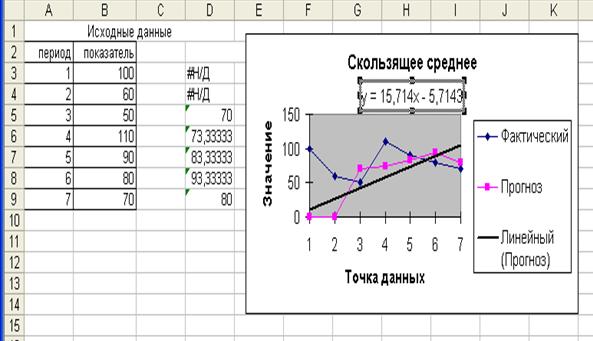
С помощью полученного уравнения У=15,714х – 5,7143 получим прогнозное значение У = 15,714*10 – 5,7143 = 151,43 – прогнозное значение объёма ВРП в следующем году.
Метод экспоненциального сглаживания, разработанный Р. Брауном,даёт возможность получить оценки параметров тренда, характеризующих не средний уровень процесса, а тенденцию, сложившуюся к моменту последнего наблюдения. Данный метод позволяет давать обоснованные прогнозы на основании рядов динамики, имеющих умеренную связь во времени, и обеспечивает большой учёт показателей, достигнутых в последние периоды наблюдения.
Суть метода заключается в сглаживании временного ряда с помощью взвешенной скользящей средней, в которой веса подчинены экспоненциальному закону. Метод экспоненциального сглаживания не просто экстраполирует действующие зависимости в будущее, а приспосабливается, адаптируется к изменяющимся во времени условиям. Поэтому он является эффективным и надёжным методом среднесрочного прогнозирования.
Рассмотрим применение метода экспоненциального сглаживания для наиболее распространённого случая, когда тренд описывается линейной функцией. В этом случае используется полином первой степени и тренд выражается двумя членами ряда Тейлора и некоторым малым числом 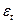 , зависящим от времени:
, зависящим от времени:
y=A+Bt+ 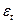 .
.
Данное выражение называют линейной моделью Брауна. При выборе начальных условий Браун рекомендует рассчитывать А, В путём выравнивания исходного временного ряда способом наименьших квадратов.
Процесс экспоненциального сглаживания основывается на цепочечных расчётах. Сначала устанавливаются исходные параметры выравнивающих кривых А,В, по которым с помощью формул находятся начальные условия. На основе этих условий по формулам определяются характеристики сглаживания, затем – оценки коэффициентов для экспоненциального сглаживания первого порядка в исходном динамическом ряду и, наконец, расчётное значение линейной (y=A+Bt). Полученные на первом этапе характеристики сглаживания затем используются в качестве исходных данных для вычисления второго сглаженного значения в рассматриваемом динамическом ряду и т.д. Вычисления продолжаются до тех пор, пока не будут сглажены все значения исходного временного ряда.
Коэффициенты уравнения (оценки коэффициентов), найденные при экспоненциальном сглаживании последнего значения в исходном динамическом ряду, используются для последующего прогноза.
Начальные приближения для случая линейного тренда равны:
экспоненциальная средняя 1-го порядка:
S 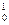 (y)=A -
(y)=A - 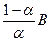 ;
;
экспоненциальная средняя 2-го порядка:
S 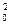 (y)=A -
(y)=A - 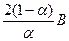 ,
,
где 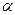 – параметр сглаживания.
– параметр сглаживания.
В зависимости от величины параметра прогнозные оценки по-разному учитывают влияние исходного ряда наблюдений: чем больше 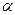 , тем больше вклад последних наблюдений в формирование тренда, а влияние начальных условий убывает быстро. При малом
, тем больше вклад последних наблюдений в формирование тренда, а влияние начальных условий убывает быстро. При малом 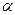 прогнозные оценки учитывают все наблюдения, при этом уменьшение влияния более ранней информации происходит медленно.
прогнозные оценки учитывают все наблюдения, при этом уменьшение влияния более ранней информации происходит медленно.
Для приближённой оценки 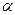 используют соотношение Брауна:
используют соотношение Брауна:
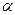 =
= 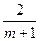 ,
,
где m – число наблюдений (точек) в ретроспективном динамическом ряду.
Зная начальные условия S 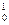 (y), S
(y), S 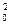 (y) и значение параметра
(y) и значение параметра 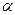 , вычисляют экспоненциальные средние 1-го и 2-го порядка:
, вычисляют экспоненциальные средние 1-го и 2-го порядка:
S 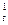 (y)=
(y)= 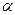 yt + (1-
yt + (1- 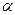 ) S
) S 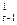 (y);
(y);
S 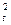 (y)=
(y)= 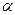 S
S 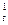 + (1-
+ (1- 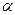 ) S
) S 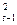 (y).
(y).
Оценки коэффициентов линейного тренда:
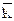 = 2 S
= 2 S 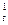 (y) - S
(y) - S 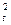 (y);
(y);
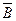 =
= 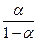 [ S
[ S 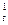 (y)- S
(y)- S 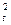 (y)].
(y)].
Прогноз на время t равен:
yt= 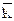 +
+ 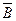 *t.
*t.
Ошибка прогноза:
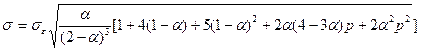 ,
,
где p – период прогноза.
Рассмотрим пример: Пусть задан временной ряд объёма расходов на капитальный ремонт в жилищно-коммунальном хозяйстве города за 5 лет в млн руб. в сопоставимых ценах (таблица 3.3):
Таблица 3.3 – Динамика расходов на капитальный ремонт в жилищно-коммунальном хозяйстве города, млн руб.
| t | |||||
| показатель |
Используя метод экспоненциального сглаживания построить прогноз ожидаемого объёма финансовых расходов на капитальный ремонт в ЖКХ города.
Согласно имеющейся динамике показателя расходов, можно предположить что тренд описывается линейной функцией.
Рассмотрим решение задачи средствами Excel.
1. Заносим статистические данные на лист Excel.
2. В меню ДАННЫЕ выберите команду АНАЛИЗ ДАННЫХ.
Если раздел АНАЛИЗ ДАННЫХ отсутствует, то его необходимо установить. Для установки раздела АНАЛИЗ ДАННЫХ в пакете Excel необходимо выполнить следующее:
А) в меню ФАЙЛ выберите команду ПАРАМЕТРЫ, далее НАДСТРОЙКИ;
Б) в появившемся списке установите флажок ПАКЕТ АНАЛИЗА.
3. В открывшемся диалоговом окне АНАЛИЗ ДАННЫХ выберите инструмент ЭКСПОНЕНЦИАЛЬНОЕ СГЛАЖИВАНИЕ Þ ОК.
4. В диалоговом окне ЭКСПОНЕНЦИАЛЬНОЕ СГЛАЖИВАНИЕ необходимо определить следующие параметры:
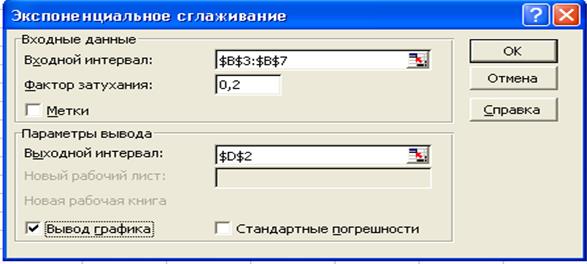
· В поле Входной интервал укажем диапазон с исходными данными (В3:В7).
· Укажем Фактор затухания равный 0,2.
· Установим курсор в поле Выходной интервал, мышкой укажем любую ячейку, например D2 .
· Установим флажок на команде вывод графика.
· После того как все параметры заданы, щёлкнем по кнопке ОК, Excel выполнит все необходимые вычисления и разместит результаты на листе.
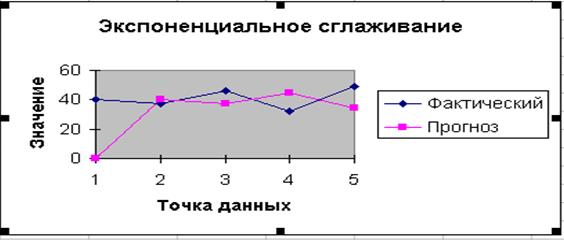
5. Правой кнопкой мыши нажмите на одно из значений графика Прогноза. Далее в диалоговом окне выберите Добавить линию тренда.
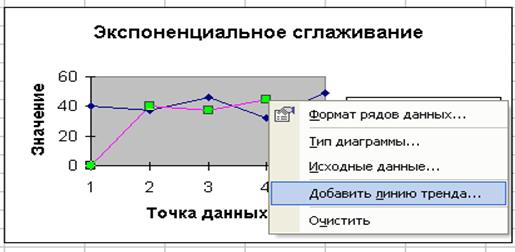
6. В диалоговом окне Линия тренда выберите тип предполагаемой зависимости, например, предположим, что зависимость линейная. Далее выберите команду Параметры, в появившемся диалоговом окне отметьте флажок на команде Показать уравнение на диаграмме.
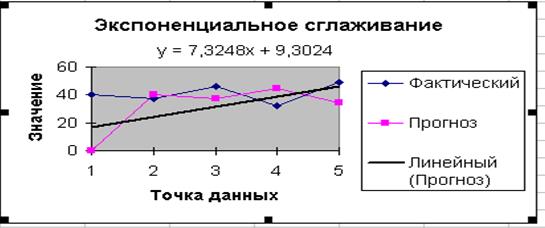
С помощью полученного уравнения У= 7,3248х + 9,3024 получим прогнозное значение У = 7,3248*6 + 9,3024, где «6» период прогноза. Получим 53,25 млн руб. – прогнозное значение объёма расходов на капитальный ремонт в ЖКХ города на следующий год.
Дата добавления: 2020-03-17; просмотров: 924;











