Приведение моментов и моментов инерции
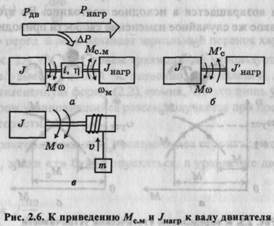
Простая модель механический части (см. рис. 2.1), использовавшаяся выше и позволившая получить полезные сведения, разумеется, применима непосредственно лишь к ограниченному числу электроприводов. Обычно между двигателем и нагрузкой находится какая-либо механическая передача (см. рис. 1.1, 1.2), т.е. имеется несколько различных валов со своими моментами и скоростями. Для сведения любой реальной системы к простейшей модели на рис. 2.1 нужно выполнить ряд операций, называемых приведением моментов и моментов инерции к некоторому выбранному в качестве основного валу, обычно — к валу двигателя. Иными словами, некоторую реальную механическую систему, например показанную на рис. 2.6, я, нужно заменить эквивалентной системой (рис. 2.6, б), такой, чтобы эта замена не отразилась на поведении части системы, оставленной неизменной (в примере — двигателя).
Примем следующие допущения: система жесткая, без зазоров; моменты инерции, относящиеся к основным валам, неизменны, относящиеся к промежуточным валам, если такие есть, малы и практически равны нулю; отношение скоростей двигателя и механизма (нагрузки) 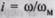 и КПД передачи
и КПД передачи 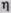 постоянны.
постоянны.
В реальной и приведенной системах (рис. 2.6, а, б) должна остаться неизменной мощность, развиваемая двигателем 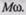 При отсутствии потерь в передаче
При отсутствии потерь в передаче
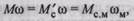
где 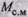 — статический момент на валу механизма (нагрузки).
— статический момент на валу механизма (нагрузки).
В нашем случае, когда потери покрываются двигателем (  на-
на-
правлены согласно), 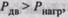 т.е.
т.е.
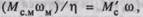
откуда

Потери всегда покрываются той частью системы, которая создает движение, поэтому при обратном потоке мощности — от нагрузки к двигателю

В реальной и приведенной системах должны быть одинаковы запасы кинетической энергии, т.е.
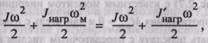
или

Здесь в целях упрощения мы не учли потери в передачах; это обычно не приводит к большим погрешностям, если динамические режимы не играют определяющую роль в работе привода.
Операция приведения может, разумеется, производиться, если один из элементов, например поднимаемый груз (рис. 2.6, в), движется поступательно. При этом сохраняются изложенные выше правила: мощность элемента, к которому приводятся другие, не должна измениться и должен быть одинаковым запас кинетической энергии в исходной и приведенной системах. Тогда, если движение создается двигателем,

т.е.

где  — масса груза;
— масса груза; 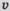 — скорость перемещения груза;
— скорость перемещения груза; 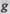 — ускорение свободного падения;
— ускорение свободного падения;  — радиус приведения. Приравняв запасы кинетической энергии
— радиус приведения. Приравняв запасы кинетической энергии

получим
Рассмотренные простые приемы приведения моментов (сил) и моментов инерции (масс) позволяют решать различные практические задачи. Часто нагрузка — технологическая машина или механизм — бывает известна, т.е. известны 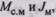 и требуется подобрать двигатель и передачу, удовлетворяющие заданному критерию, например минимальным потерям (наибольшему КПД) или минимальной массе, минимальной стоимости и др., при оговоренных ограничениях — доступное оборудование с его каталожными данными и т.п. Иногда бывают известны нагрузка и двигатель и требуется подобрать передачу, наилучшим образом обеспечивающую постав
и требуется подобрать двигатель и передачу, удовлетворяющие заданному критерию, например минимальным потерям (наибольшему КПД) или минимальной массе, минимальной стоимости и др., при оговоренных ограничениях — доступное оборудование с его каталожными данными и т.п. Иногда бывают известны нагрузка и двигатель и требуется подобрать передачу, наилучшим образом обеспечивающую постав 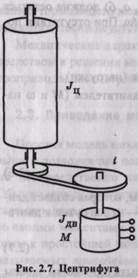 ленную
ленную  технологическую задачу.
технологическую задачу.
Рассмотрим в качестве примера одну из таких
задач. Пусть имеются центрифуга (рис. 2.7) с известным моментом инерции 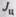 и пренебрежимо малым моментом сопротивления
и пренебрежимо малым моментом сопротивления  и двигатель с извест-
и двигатель с извест-
ными  Нужно подобрать передачу с передаточным числом
Нужно подобрать передачу с передаточным числом 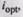
обеспечивающим центрифуге максимальное ускорение
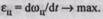
Запишем уравнение движения (2.3) для центрифуги:
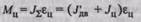
и подставим в него величины 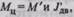 приведенные к валу центрифуги в со-
приведенные к валу центрифуги в со-
ответствии с изложенными выше правилами при пренебрежении потерями в передаче. Получим
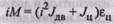
или
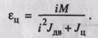
Искомое передаточное отношение 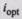 найдем, продифференцировав последнее выражение по i и приравняв производную нулю:
найдем, продифференцировав последнее выражение по i и приравняв производную нулю:
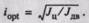
Последние два выражения служат основой для проектирования механической части системы двигатель — передача — центрифуга.
Дата добавления: 2020-03-17; просмотров: 477;











