Виды граничных условий

Из курса высшей математики известно, что дифференциальные уравнения, как правило, имеют бесконечное множество решений. Это связано с появлением в процессе интегрирования констант, при любых значениях которых решение удовлетворяет исходному уравнению.

Приведем пример. Для этого рассмотрим уравнение теплопроводности для двумерного случая:

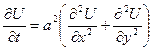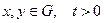, , (4.15)

где 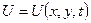– температура, функция пространственных координат 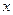, 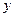и температуры 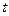; 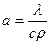, 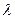– коэффициент теплопроводности, 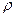– удельная плотность, 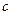– теплоемкость материала.

Общим решением уравнения (4.15) будет являться следующая функция:

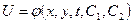. (4.16)

Особенностью задач матфизики является то, что все найденные зависимости от координат и времени должны удовлетворять следующим требованиям:

- однозначности – физическая величина не может иметь двух или более различных значений в данной точке пространства и в данный момент времени;

- конечности – физическая величина не может иметь бесконечных по модулю значений;

- непрерывности.

Поэтому математическая формулировка физической задачи должна помимо основных уравнений (дифференциальных уравнений в частных производных), описывающих искомые функции внутри рассматриваемой области, включать дополнительные уравнения (дифференциальные или алгебраические), описывающие искомые функции на границах рассматриваемой области в любой момент времени во всех внутренних точках области в начальный момент времени. Эти дополнительные условия называют соответственно граничными и начальными условиями задачи. По виду уравнений, задающих граничные условия, различают граничные условия первого, второго, третьего и четвертого рода.