Способы преобразования ортогонального чертежа

Решение позиционных и метрических задач становится проще, если геометрические фигуры находятся в частном положении относительно плоскостей проекций. Для того, чтобы геометрические фигуры заняли частное положение, необходимо выполнить преобразование чертежа. Существует два основных способа преобразования ортогонального чертежа:

- способ введения дополнительных плоскостей проекций;

- способ вращения вокруг прямой (или проецирующей или прямой уровня).

Сущность первого способа заключается в том, что геометрический объект пространства вместе с системой координат не меняет своего положения в пространстве, а новая плоскость проекций П₃ П₁ (или П₃ П₂) занимает частное положение по отношению к заданному объекту.

Во втором случае плоскости проекций не меняют своего положения в пространстве, а геометрический объект путем поворота вокруг надлежаще выбранной оси занимает частное положение по отношению к плоскостям проекций. Частной разновидностью способа вращения является и способ плоско-параллельного перемещения.

Рассмотрим первый способ – способ замены плоскостей проекций. Суть способа состоит во введении новой дополнительной плоскости проекций П₃ перпендикулярной одной из исходных плоскостей (либо П₁ либо П₂). Заданные геометрические фигуры ортогонально проецируют на новую плоскость проекций.

Рассмотрим схему построения чертежа на примере проецирования точки А на дополнительную плоскость П₃ П₁ (рис. 5.1,а).

Прямую пересечения новой плоскости П₃ с исходной П₁ принимаем за новую ось проекции. Вращением на 90° вокруг новой оси П₁/П₃ совмещаем новую плоскость проекций П₃ с плоскостью П₁ на первом этапе. Затем на втором этапе совмещаем эти объединенные плоскости с плоскостью П₂ поворотом на 90° вокруг оси П₂/П₁ Можно сказать, что в этом случае плоскость чертежа совмещается с фронтальной плоскостью проекций П₂.

Алгоритм построения чертежа точки (рис. 5.1,б):

1. Проводим ось проекций П₁/П₃;

2. Строим новую линию проекционной связи из точки A₁ перпендикулярную оси П₁/П₃;

3. Откладываем от точки Пересечения новой линии проекционной связи с осью П₁/П₃ высоту точки A (аппликату Z), равную расстоянию от A₂ до старой оси П₁/П₂

Из рассмотренного промера можно вывести общие свойства чертежа с дополнительными плоскостями проекций:

1. Линии связи перпендикулярны осям проекций;

2. Расстояние от старой не общей проекции А₂ до старой оси равно расстоянию от новой оси до новой проекции А₃. [Легче данное правило запомнить с помощью следующей мнемонической формулировки: «Рукава рубашки должны быть равны»]. Рассмотрим аналогичную задачу проецирования точки А на новую дополнительную плоскость П₄ перпендикулярную П₂ (рис. 5. 2).

Для этого вводим новую ось проекций П₂/П₄. Из точки А₂ проводим новую линию проекционной связи, перпендикулярную оси П₂/П₄, на ней от точки пересечения линии проекционной связи с осью П₂/П₄ откладываем ординату точки A, равную расстоянию от A₁ до оси П₁/П₂. Для решения некоторых задач достаточно выполнить одну замену плоскостей проекций. Решение других задач могут потребовать выполнения двух замен и более. Мы можем вводить любое количество дополнительных плоскостей проекций. Причем они вводятся последовательно друг за другом для замены уже введенных дополнительных плоскостей проекций.

На рисунке ниже можно видеть, что вначале вводится дополнительная плоскость проекций П₃ П₁, а затем новая плоскость П₄ П₃.

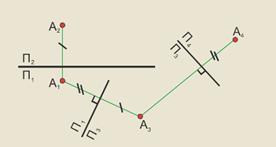
Определить длину отрезка AВ и угол его наклона к плоскости проекций можно путем введения одной дополнительной плоскостей проекций, причем расположить ее так, чтобы она была параллельна исходному отрезку. При этом дополнительная плоскость П₃ может быть перпендикулярной либо к П₁ либо П₂. Это зависит от того, какой угол наклона мы должны определить.

Рассмотрим пример (рис.5.4), когда необходимо определить длину отрезка АВ и его угол наклона к плоскости П₁ (угол a).

Алгоритм графических построений:

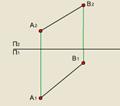
Вводим дополнительную плоскость П₃ || АВ и одновременно П₃ П₁ (для определения угла a). Для этого проводим ось проекций П₁/П₃ параллельно A₁B₁;

1. Проводим линии проекционной связи в системе плоскостей проекции П₁ - П₃ перпендикулярно оси П₁/П₃;
2. Откладываем на них от оси П₁/П₃ расстояния равные расстояниям от А₂ и B₂ до оси П₁/П₂;
3. Соединяем А₃ и B₃. Длина проекции А₃B₃ равна длине отрезка |АВ|. Угол a – угол наклона А₃B₃ к оси П₁/П₃ - равен углу наклона АВ к плоскости проекций П₁

Если нам требуется найти угол наклона отрезка AB к плоскости П₂ (угол b), то дополнительную плоскость проекций П₃ следует вводить параллельно A₂B и перпендикулярно П₂. Все построения аналогичны.