Коммутационные функции
Для сокращения записи страховых аннуитетов и упрощения расчетов применяют так называемые коммутационные функции или коммутационные числа. Смысл этих чисел трудно, хотя и возможно, содержательно интерпретировать. Их проще воспринимать как чисто технические, вспомогательные средства.
Стандартные коммутационные функции делятся на две группы. В основу первых положены числа доживающих до определенного возраста, вторых – числа умерших. Основными в первой группе являются функции Dx и Nx:
Dx=lxvx, Nx= 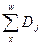
где v – дисконтный множитель по сложной ставке i , w - предельный возраст, учитываемый в таблице смертности.
По определению Nx=Nx+1+Dx, NW=Dw.
В некоторых актуарных расчетах необходимы суммы коммутационных чисел Dx для заданных возрастных интервалов. В этих случаях можно воспользоваться коммутационными числами Nx:

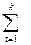 Dx+t=Nn+1 – Nx+k+1
Dx+t=Nn+1 – Nx+k+1
На практике применяются еще два варианта функции Nx, к которым обращаются тогда, когда платежи производятся m раз в году. Так, для платежей постнумерандо с достаточной для практических расчетов точностью применим следующее выражение:
Nx(m)»Nx+(m-1)/2m*Dx.
Для платежей пренумерандо
Nx(m)»Nx+(m-1)/2m*Dx.
Наиболее важными коммутационными функциями второй группы являются Cx
и Mx: Cx=dxvx+1, Mx= 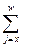 Cj
Cj
Между коммутационными числами обеих групп существуют определенные взаимозависимости:
Cx=dxvx+1=(lx-lx+1)vx+1=lxvxv – lx+1vx+1=Dxv-Dx+1.
Аналогично можно доказать, что
Mx=Nxv – Nx+1.
Страховые организации разрабатывают таблицы коммуникационных функции с учетом принятых в них норм доходности.
Таблица 4.2 Фрагмент таблицы коммутационных чисел
| x | lx | Dx | Nx | Nx(12) | Cx | Mx |
| 100 000 | 21 199 | 244 593 | 245 309 | 28,98 | 1003,6 | |
| 99 851 | 19 420 | 223 393 | 232 294 | 30,82 | 974,7 | |
| 99 678 | 17 786 | 203 973 | 212 125 | 31,98 | 943,8 | |
| … | ||||||
| 96 991 | 80 677 | 84 027 | 25,55 | 648,9 | ||
| … | ||||||
| 94 951 | 49 910 | 52 042 | 20,78 | 530,3 | ||
| … | ||||||
| 92 327 | 30 376 | 31 723 | 19,09 | 431,4 | ||
| … | ||||||
| 83 640 | 10 465 | 10 981 | 14,54 | 206,7 | ||
| … | ||||||
| 68 505 | 10,25 | 134,7 | ||||
| … | ||||||
| 45 654 | 5,72 | 53,1 | ||||
| … | ||||||
| 19 760 | 2,14 | 13,0 |
При страховании супружеских пар возникает необходимость в коммутационной функции:
Dxy=lxy*v(x+y)/2.
Величина lxy определена при расчете nPxy
Функцию Dxy=lxy*v(x+y)/2 можно получить на основе коммутационной функции Dx, Dy следующим образом:
Dxy=Dx*Dy*v-(x+y)/2=Dx*Dy*(1+I)(x+y)/2.
В свою очередь
Dxy+n=lxy+n*vn+(x+y)/2.
Dxy+n=Dx+n*Dy+n*v-[n+(x+y)/2]=Dx+n*Dy+n*(1+I)n+(x+y)/2.
Поскольку произведение коммутационных чисел имеют большую размерность, то их обычно умножают на 10-3.
Пример: определим коммутационные числа D50;45 и D55;50 для супружеской пары возраст супругов 50 и 45 лет. Находим:
(x+y)/2=(50+45)/2=47,5.
Коммутационные числа при условии, что процентная ставка равна 9%, имеют следующие значения (первая строка – для мужчины, вторая – для женщины):
D50=1124,8; D55=673,1;
D45=1991,9 D50=1268,8.
Отсюда
D50;45=10-3*1124,8*1991,9*1,0947,5=134 308;
D55,50=10-3*673,1*1268,8*1,095+47,5=78 770.
По аналогии с функцией Nx найдем: Nxy= 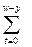 Dx+t; y+t.
Dx+t; y+t.
Тестовые задания
4011324. Аннуитет – это:
1. Период времени между двумя последовательными платежами;
2. Последовательность периодических платежей, сделанных через различные промежутки времени;
3. Последовательность периодических платежей, сделанных через одинаковые промежутки времени;
4 Одноразовый платёж.
4023142. Срок аннуитета – это:
1. Время от начала первого интервала платежа до начала последнего интервала платежа;
2. Время от начала первого интервала платежа до окончания последнего интервала платежа;
3. Время от окончания первого интервала платежа до начала последнего интервала платежа;
4. Нет правильного ответа.
4032314. Аннуитет называется обыкновенным, если:
1. Срок платежа осуществляется в моменты окончания интервалов платежа;
2. Срок платежа осуществляется в начальный момент интервала платежа;
3. Интервал платежа совпадает с периодом начисления процента;
4. Срок не имеет значения, все зависит от суммы платежа.
4041234. Настоящая стоимость обыкновенного аннуитета определяется как:
1. Датированная сумма эквивалентная всей серии платежей независимо от срока аннуитета;
2. Датированная сумма эквивалентная всей серии платежей на начало срока аннуитета;
3. Сумма всех платежей;
4. Сумма всех платежей без учета срока платежей.
4052314. Итоговая сумма обыкновенного аннуитета определяется как:
1. Датированная сумма эквивалентная всей серии платежей на начало срока;
2. Датированная сумма эквивалентная всей серии платежей на конец срока;
3. Сумма всех платежей;
4. Сумма всех платежей без учета срока платежей.
4063142. Аннуитет называется простым, если:
1. Срок платежа осуществляется в момент, обусловленный договором;
2. Интервал платежа совпадает с периодом начисления процента;
3. Срок платежа осуществляется в момент окончания интервала платежа;
4. Периодический платеж производится в начальный момент времени.
4073142. Аннуитет называется страховым, если:
1. Выплата ренты не зависит от наступления страхового события, а зависит лишь от времени уплаченной страховой суммы;
2. Выплата ренты зависит от наступления страхового события;
3. Выплата ренты не зависит от наступления страхового события при условии, что страхователь назвал наследника;
4. Нет правильного ответа.
4082413. Полагающий аннуитет – это:
1. Когда периодические платежи производятся в начальные моменты интервалов платежа, со сроком, начинающимся датой первого и заканчивающимся через один интервал после последнего платежа;
2. Когда периодические платежи производятся в конечные моменты интервала и заканчиваются за один интервал до даты погашения;
3. Когда интервал платежа совпадает с периодом начисления процента;
4. Нет правильного ответа.
Факторами определяющими стоимость страхового аннуитета являются: а) демографический, отражаемый в таблице смертности; б) процентная ставка (установленная норма доходности); в) длительность отсрочки выплат; г) срок аннуитета.
1. а, б, в;
2. б, в, г;
3. а, в, г;
4. а, б, в, г.
4101324. Аннуитет называется отсроченным, если:
1. Срок аннуитета не изменяется;
2. Срок аннуитета устанавливается с даты заключения сделки;
3. Срок аннуитета устанавливается с даты в будущем относительно даты заключения сделки;
4. Интервал платежа совпадает с периодом начисления процента.
4111234. Чем выше показатель смертности:
1. Тем выше страховая (актуарная) стоимость аннуитета;
2. Тем ниже страховая (актуарная) стоимость аннуитета;
3. Страховая (актуарная) стоимость аннуитета не меньше;
4. Нет правильного ответа.
Дата добавления: 2020-02-05; просмотров: 754;











