Минимизация функций
Запись функции в СДНФ не единственно возможная и, как правило, не самая короткая. Чем меньше элементов содержит аналитическое выражение, тем проще логическая схема.
Выражение (1.1) можно упростить, если добавить в него дважды abc (закон тавтологии), сгруппировать попарно слагаемые (сочетательный закон) и исключить (закон склеивания) переменные, которые в группе меняют свои значения.
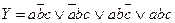
 abc
abc  abc= (abc
abc= (abc  a
a  c)
c) 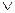 (abc
(abc 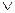
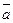 bc)
bc) 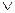 (abc
(abc 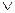 ab
ab  ) =
) =

= ac(b 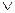
 )
) 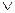 bc(a
bc(a 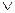
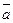 )
) 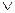 ac(c
ac(c 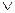
 ) = ac
) = ac 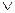 bc
bc 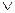 ac (1.2)
ac (1.2)
Рис. 1.7. Схема, реализующая (1.2).
a) в булевском базисе; б) в базисе И-НЕ.
В инженерной практике для минимизации наиболее часто применяют карты Карнау (Карно).
Карты Карно – это графическое представление таблиц истинности логических функций. Структура карт для функций двух, трех и четырех переменных показана ниже.
Таблица истинности (а) и структура карты Карно (б) для функции двух переменных.
| x1 | x2 | f(x1,x2) |
| f(0,0) | ||
| f(0,1) | ||
| f(1,0) | ||
| f(1,1) |
| x2 | |||
| x1 | |||
| f(0,0) | f(0,1) | ||
| f(1,0) | f(1,1) |
|
|
Таблица истинности (а) и cтруктура карты Карно (б) для функции трех переменных.
| x1 | x2 | x3 | f(x1,x2,x3) |
| f(0,0,0) | |||
| f(0,0,1) | |||
| f(0,1,0) | |||
| f(0,1,1) | |||
| f(1,0,0) | |||
| f(1,0,1) | |||
| f(1,1,0) | |||
| f(1,1,1) |
| а) |
| x2,x3 | |||||
| x1 | |||||
| f(0,0,0) | f(0,0,1) | f(0,1,1) | f(0,1,0) | ||
| f(1,0,0) | f(1,0,1) | f(1,1,1) | f(1,1,0) |
|
Сократить работу по минимизации иногда можно за счет работы не с самой заданной функцией, а с ее инверсией. Если число единиц в таблице истинности превышает половину числа комбинаций аргументов, то СДНФ для инверсии функции будет содержать меньше конъюнкций, чем СДНФ прямой функции. При аппаратной реализации к выходу схемы, обрабатывающей инверсию заданной функции, нужно подключить инвертор.
Пример.
Построить схему, реализующую функцию, заданную таблицей:
| a | b | c | Y | 
| a | B | c | y | 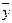
|
СДНФ требуемой функции: 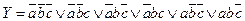
Для  СДНФ будет значительно проще:
СДНФ будет значительно проще: 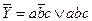 .
.
Последнее выражение более обозримо и легко минимизируется:
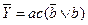 = ac, откуда
= ac, откуда  .
.
Для реализации необходим один двухвходовой элемент 2И–НЕ.
Рассмотрим особенности минимизации недоопределенныхфункций.
Недоопределенной называют функцию, значения которой при некоторых комбинациях не определены или, как говорят, безразличны. Например, при двоично-десятичном кодировании десятичные цифры представляются четырьмя двоичными разрядами. Из 16 возможных кодовых комбинаций используются лишь 10, остальные запрещены и никогда появиться не могут.
В таблице истинности не определенные значения функции отмечают прочерками.
Пример.
Построить схему, реализующую функцию Y, не определенную на наборах 000 и 111 и заданную таблицей.
 Y Y
| bc | |||||
| a | ||||||
| – | ||||||
| – | ||||||
При двух прочерках возможны четыре способа доопределения. Каждый из них дает работоспособную схему, но по аппаратурным затратам они будут разными. Самая простая схема получится, если доопределить функцию так, как показано на рис. 1.8,а.
В этом случае схема строится на двух ЛЭ: 2И и 2ИЛИ. (рис. 1.9.б)
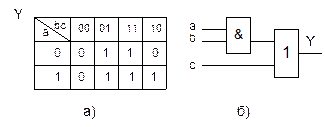
Рис. 1.9.Реализация недоопределенной функции.
Дата добавления: 2020-02-05; просмотров: 733;











