Логические функции.
Функции АЛ принимают значения 1 или 0 в зависимости от значений своих аргументов. Одна из форм задания логической функции - табличная. Таблицы, отображающие соответствие всех возможных комбинаций значений двоичных аргументов значениям логической функции, называют таблицами истинности.
Как бы ни была сложна логическая связь между логической функцией и ее аргументами, эту связь всегда можно представить в виде совокупности трех простейших логических операций: НЕ, И, ИЛИ. Этот набор называют булевским базисом, в честь английского математика Д.Буля (1815-1864), разработавшего основные положения АЛ.
Функция НЕ (другие названия: отрицание, инверсия) - это функция одного аргумента. Она равна 1, когда ее аргумент равен 0, и наоборот. Обычное обозначение Q=  . Встречаются и другие обозначения Q=НЕ
. Встречаются и другие обозначения Q=НЕ 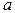 , Q=
, Q=  . Читается «Q есть не а».
. Читается «Q есть не а».
Электронный логический элемент (ЛЭ), реализующий функцию НЕ в виде определенных уровней напряжения, называют инвертором. Инвертор на схемах изображается, как показано на рис. 1.3,а. Вход- слева, выход- справа, кружок- символ инверсии. Условное изображение инвертора (или любого другого ЛЭ) на схеме может быть повернуто на 90° (вход- сверху, выход- снизу, рис. 1.3,б). Другие углы поворота и направления входов и выходов не допускаются.
В релейно-контактной технике функцию НЕ реализует нормально замкнутый контакт (рис. 1.3,в), т.е. такой контакт реле, который замкнут, пока в обмотке нет токового сигнала 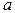 , и размыкается при подаче тока
, и размыкается при подаче тока 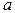 .
.
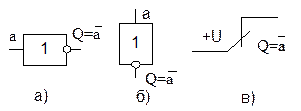
Рис.1.3. Инвертор
а) предпочтительное изображение
б) допустимое изображение
в) реализация НЕ в релейно-контактной технике
Функция И (другие названия: конъюнкция, логическое умножение, AND)- это функция двух или большего числа аргументов.
Обозначение: Q=a&b; Q=aÙb; Q=a×b; Q=ab. Читается «Q есть a и b».
Функция И равна 1 тогда и только тогда, когда все ее аргументы равны 1. В релейно-контактной технике функция И реализуется последовательным включением нормально разомкнутых контактов (рис. 1.4,а). Ток в цепи пойдет, когда контакты замкнуты, т.е. находятся в единичном состоянии.
Значения функции И для всех комбинаций аргументов a и b приведены в таблице 1.1. Там же приведены значения и других часто используемых функций, о которых речь будет вестись ниже.
Элемент, реализующий функцию И, называют элемент И или конъюнктор. Элемент И часто используют для управления потоком информации. При этом на один его вход поступают логические сигналы, несущие некоторую информацию, а на другой- управляющий сигнал: пропускать- 1, не пропускать-0. Элемент И, используемый таким образом, называют вентиль (gate).
Таблица 1.1
| Аргументы | Функции | ||||||
| а | b | И | ИЛИ | И-НЕ | ИЛИ-НЕ | М2 | º |
Функцию И можно построить от любого числа аргументов. На рис. 1.2,б и в показаны условные изображения двух- и четырехвходового конъюнкторов.
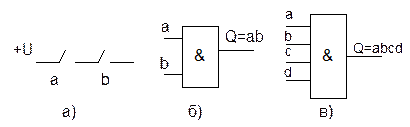
Рис. 1.4. Конъюнктор
а) реализация операции И на контактах реле
б) условное изображение двухвходового конъюнктора 2И (AND2)
в) то же для четырехвходового- 4И (AND4)
Функция ИЛИ (другие названия: дизъюнкция, логическое сложение, OR)- это функция двух или большего числа аргументов. Функция ИЛИ равна 1, если хотя бы один из ее аргументов равен 1. Обозначение: Q=aÚ b, Q=a+b. Читается: «Q есть a или b». Использовать знак «плюс» можно в тех случаях, когда дизъюнкцию нельзя смешать с арифметическим суммированием и сложением по модулю 2.
Условное изображение трехвходового дизъюнктора (3ИЛИ, OR3) показано на рис. 1.5,а. В релейно-контактных схемах функция ИЛИ реализуется параллельным включением контактов (рис. 1.5,б)

Рис. 1.5. Дизъюнктор
а) условное изображение
б) реализация ИЛИ на контактах
Дата добавления: 2020-02-05; просмотров: 679;











