Цифровой фильтр устойчив, если сумма абсолютных значений отсчетов его импульсной характеристики конечна.
Из этого критерия следует, что все фильтры с конечной импульсной характеристикой абсолютно устойчивы.
Пример:
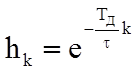 ,
,
где 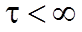 – положительная константа, от которой зависит скорость убывания отсчетов импульсной характеристики.
– положительная константа, от которой зависит скорость убывания отсчетов импульсной характеристики.
Учитывая, что 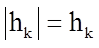 , получим
, получим
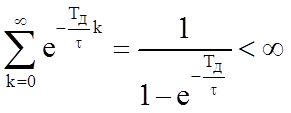 .
.
3.Критерий оценки устойчивости по системной функции фильтра
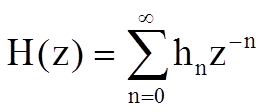 .
.
Модуль системной функции удовлетворяет неравенству
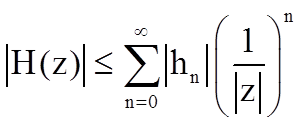 .
.
При 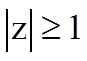 справедливо неравенство
справедливо неравенство
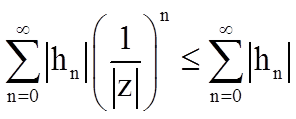 .
.
При 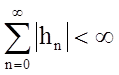 и при
и при 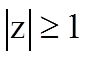
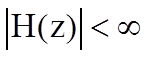 .
.
Последнее соотношение означает, что в устойчивом цифровом фильтре должны отсутствовать полюсы системной функции в области комплексной переменной z, которая удовлетворяет неравенству
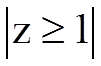
Следовательно, если полюсы существуют, то в устойчивом фильтре они должны располагаться в области комплексной переменной z, для которой выполняется условие
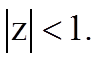
Цифровой фильтр устойчив, если полюсы системной функции располагаются внутри круга единичного радиуса с центром в начале координат 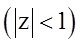 .
.
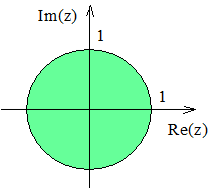
Пример 1:
На рисунке 1 дано графическое представление алгоритма функционирования цифрового фильтра. Коэффициенты системной функции равны: A = 0.5 ,
B = -1, C = -1.4.
Сделайте заключение об устойчивости фильтра
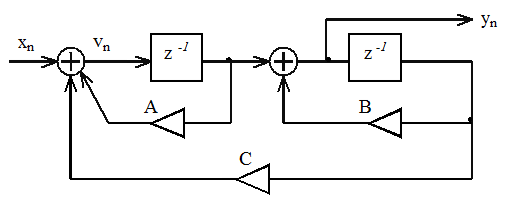
Рисунок 1
1. Из рисунка видно, что
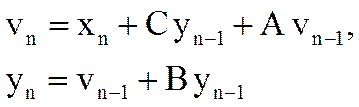
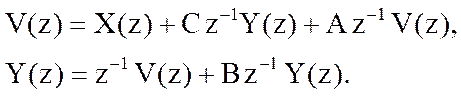
Из первого уравнения
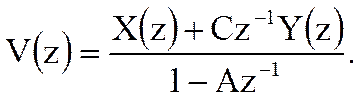
Подставим V(z) во второе уравнение
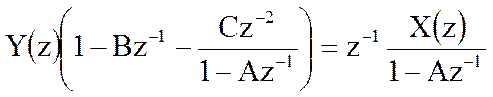
Из последнего соотношения получим
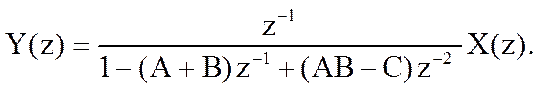
Системная функция цифрового фильтра определяется соотношением
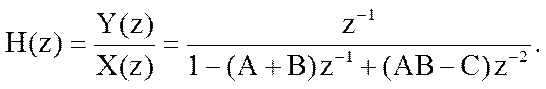
Определим полюсы системной функции. Приравняв знаменатель системной функции к нулю, получим квадратное уравнение для определения ее полюсов
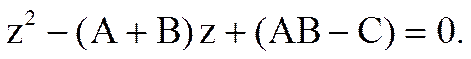
Подставляя в него значения A, B и C, получим
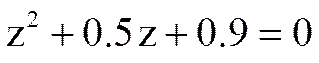 .
.
Корни уравнения равны
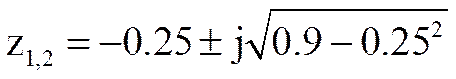 .
.
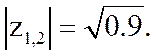 Следовательно, фильтр устойчив.
Следовательно, фильтр устойчив.
Пример 2:
Сделайте обоснованное заключение об устойчивости цифрового фильтра рисунка 1, если A11 = 0.1, A21= 0.9, A12 = - 0.1, A22 =1.1.
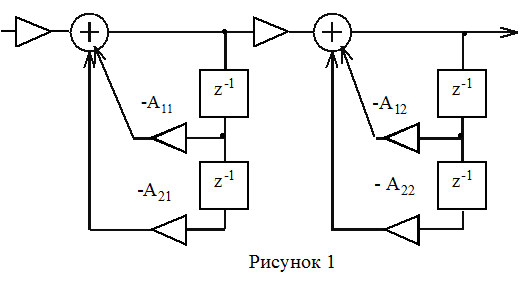
Цифровой фильтр выполнен в виде последовательного соединения двух звеньев второго порядка.
Системная функция фильтра определяется соотношением
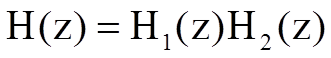 ,
,
где
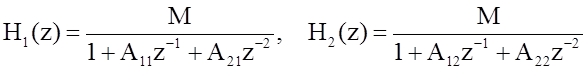 .
.
Проверяем устойчивость каждого звена.
Звено №1
 или
или
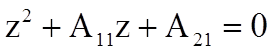
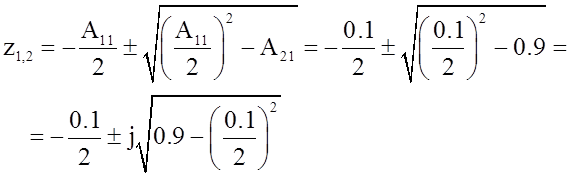
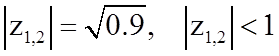 .
.
Следовательно, первое звено устойчиво.
Звено №2
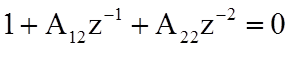 или
или
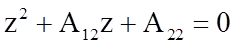
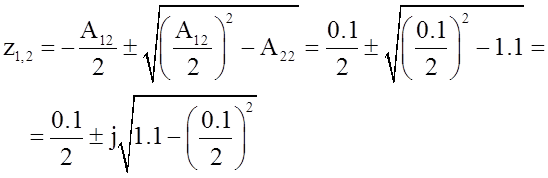
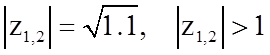 .
.
Следовательно, второе звено не устойчиво.
Вывод: фильтр не устойчив.
2.10. Коэффициенты системной функции устойчивого звена второго порядка
Системная функция звена второго порядка определяется соотношением
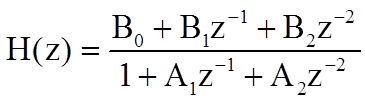 .
.
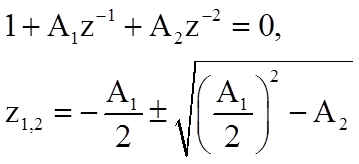
Фильтр реализуется в виде звеньев второго порядка в случае комплексно-сопряженных корней, т.е. при 
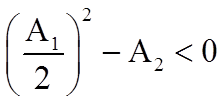 . (*)
. (*)
В этом случае корни уравнения определяются следующим соотношением
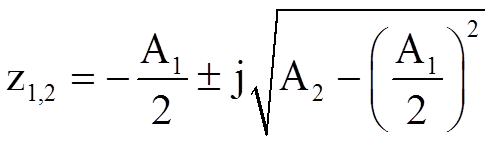 .
.
Из последнего соотношения находим
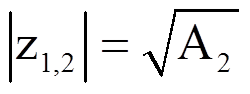 .
.
Условием устойчивости звена является
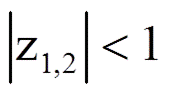 .
.
Поэтому коэффициент A2 устойчивого звена второго порядка должен удовлетворять условию
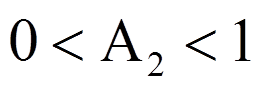
Из последнего неравенства и неравенства (*) следует
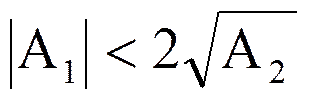
3. Преобразование Фурье
3.1.Прямое дискретное преобразование Фурье
Прямое и обратное преобразования Фурье аналогового сигнала определяются следующими соотношениями
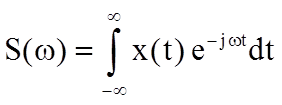
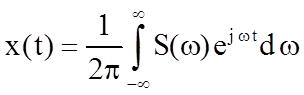
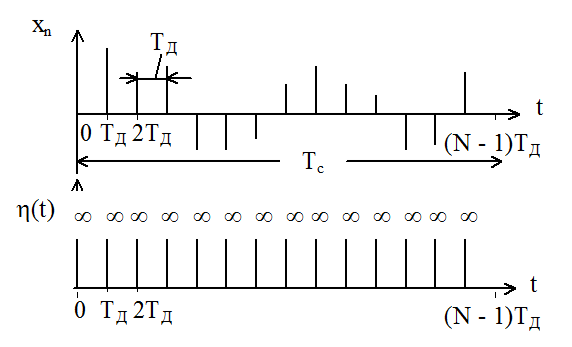
Дискретный сигнал и последовательность дельта – функций. Длительность сигнала - Tc = TД N,
Воспользовавшись последовательностью 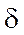 -функций, представим дискретный сигнал xn как аналоговый
-функций, представим дискретный сигнал xn как аналоговый
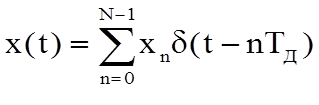
Тогда
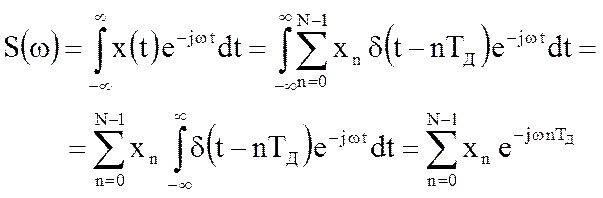
Зададимся шагом W изменения частоты w = k W , где k - целое число.
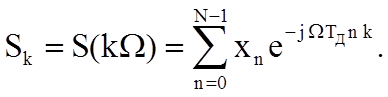
Учитывая, что TД = Tc / N , получим
W TД = 2 p F Tc / N.
Примем F Tc = 1.
Введем обозначение:

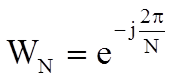
Тогда
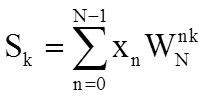
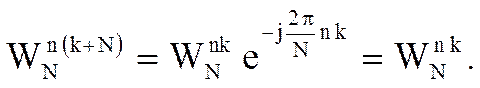
Поэтому Sk представляет собой периодическую функцию с периодом N. Поэтому k = 0,1,2,.. N-1.
3.2. Обратное дискретное преобразование Фурье
По аналогии с формулами прямого и обратного преобразования Фурье для аналогового сигнала, и учитывая выражение для Sk , сконструируем формулу для обратного дискретного преобразования Фурье
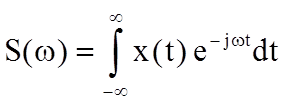
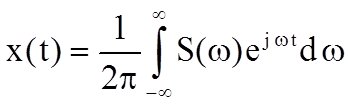
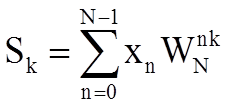
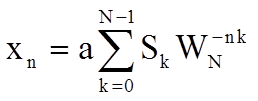
Для определения константы a подставим в последнее соотношение выражение для Sk, предварительно заменив в нем индекс суммирования n на m
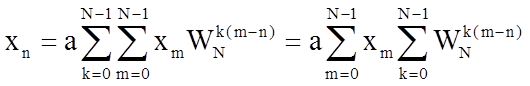 .
.
При m = n
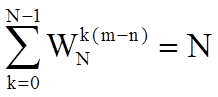
При m ¹ n
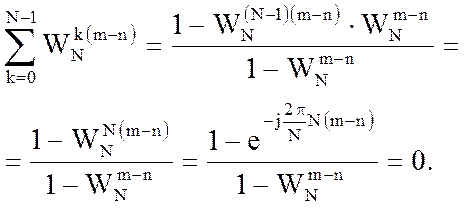
В результате получим
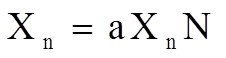 .
.
Следовательно,
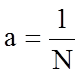
Таким образом,
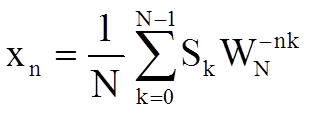
при n = 0, 1, ..N-1.
Для определения всех N отсчетов спектра или N отсчетов временной функции требуется выполнить 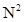 комплексных умножений и столько же комплексных сложений.
комплексных умножений и столько же комплексных сложений.
При N больше 1000 это прямое вычисление требует больших затрат машинного времени. Поэтому возникла необходимость в разработке алгоритмов быстрого преобразования Фурье (БПФ).
3.3. Алгоритм быстрого преобразования Фурье с прореживанием во времени
Рассмотрим последовательность xn, содержащую 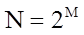 отсчетов, где M - целое число, Разобьем члены этой последовательности на две группы.
отсчетов, где M - целое число, Разобьем члены этой последовательности на две группы.
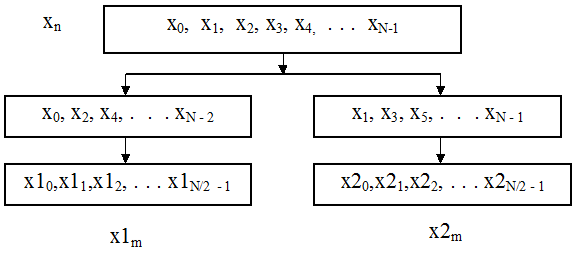
Индексы членов последовательностей xn и x1m связаны соотношением n = 2m,
а индексы членов последовательностей xn и x2m - соотношением n = 2m + 1.
Тогда выражение для прямого ДПФ можно представить в виде


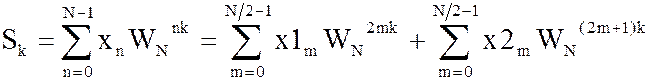
Учитывая, что

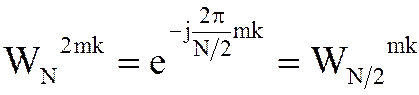 ,
,
получим
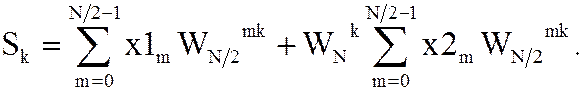
Обозначим
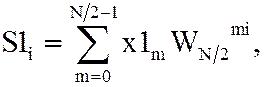
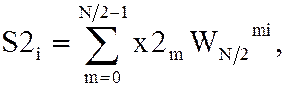
где
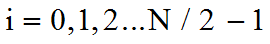 .
.
Учтем, что,
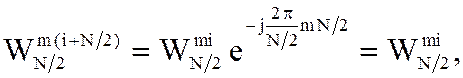
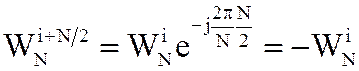
Поэтому
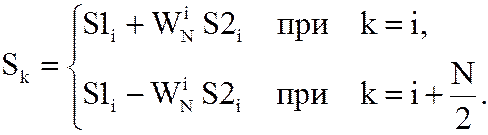
Графическое представление вычислительных операций приведено на рисунке.
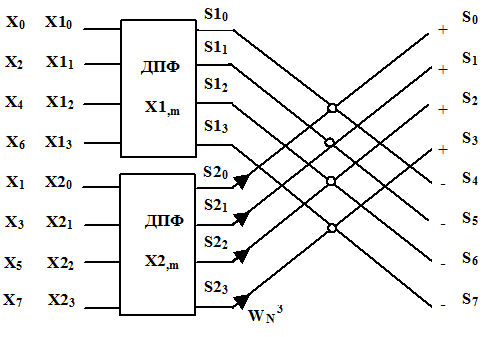
Стрелочками представлены множители
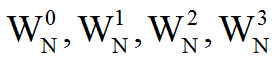 .
.
Отсчеты S0 , S1 , S2, S3 получаются с использованием операции сложения, поэтому около них стоит знак “ + “, отсчеты S4 , S5 , S6 , S7 находятся после выполнения операции вычитания и около них поставлен знак “ - “.
Подсчитаем количество операций умножения, которые нужно выполнить, используя алгоритм БПФ.
| Номер шага разбиения | Количество умножений на постоянный коэффициент | Количество блоков ДПФ, подлежащих дальнейшему разбиению | Вид последовательности на входах оставшихся блоков |
| N / 2 | N / 2 | ||
| 2 ( N / 4 ) = N / 2 | N / 4 | ||
| 4 ( N / 8 ) = N / 2 | N / 8 | ||
| . . . | . . . | . . . | . . . |
| M -1 | N / 2 | 2 M -1 | N / 2 M -1 = 2 |
| M | N / 2 | - | - |
На каждом шаге разбиения выполняется N / 2 умножений, количество шагов равно M = log 2 N.
Следовательно, количество умножений равно (N / 2) log2 N вместо N2 при ДПФ.
Величина выигрыша при переходе от ДПФ к БПФ увеличивается с увеличением количества отсчетов N.
Дата добавления: 2020-02-05; просмотров: 653;











