Цифровым фильтром называется линейная частотно-избирательная система, реализуемая на основе вычислительного устройства.

Цифровые фильтры

2.1. Свойства Z-преобразования

Прямым Z-преобразованием дискретной последовательности x_n, где n=0,1,.., называется функция комплексной переменной z, определяемая следующим соотношением

.

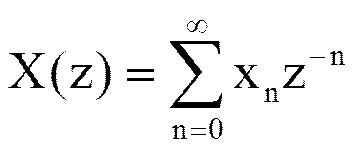Функция определена для тех значений z, при которых ряд сходится.

Здесь и в дальнейшем последовательность обозначается строчной, а ее Z-преобразование той же прописной буквой.

Пример №1:

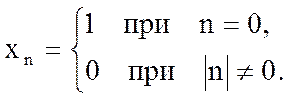
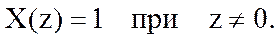
Пример №2

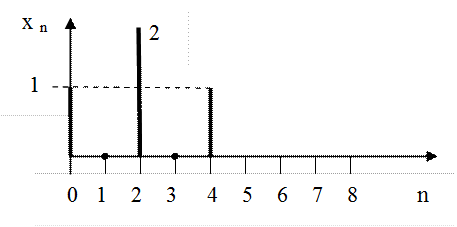
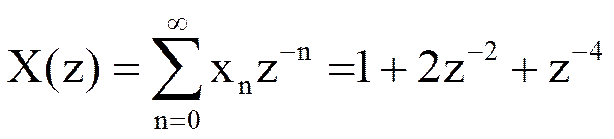
Пример №3

Найдите Z-преобразование сигнала

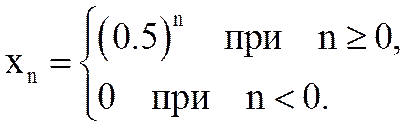
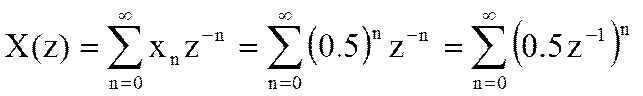При выполнении условия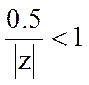

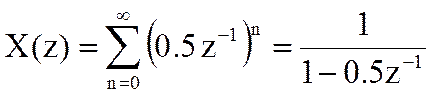
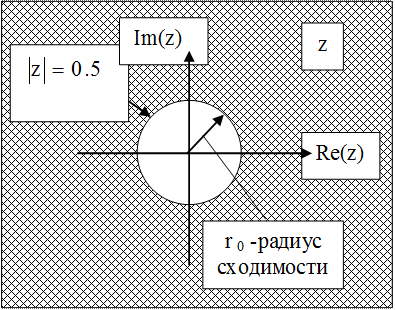
Ряд сходится в той части плоскости комплексной переменной z, для которой справедливо неравенство

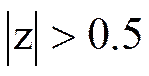
Обратное Z – преобразование

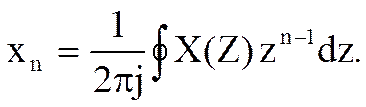
Cвойства прямого Z-преобразования.

1.Линейность. Пусть последовательность y_n представляет взвешенную сумму двух последовательностей x_1n и x_2n

,

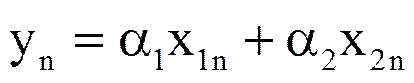где 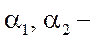постоянные весовые коэффициенты.

Тогда Z-преобразование последовательности y_n определяется следующим соотношением

.

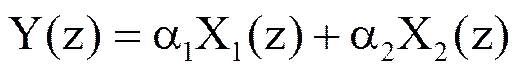Таким образом, Z-преобразование взвешенной суммы двух последовательностей равно взвешенной сумме Z-преобразований этих последовательностей.

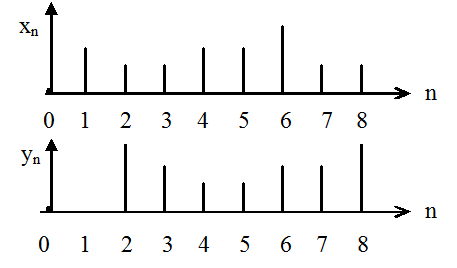
2.Сдвиг последовательностей.

.

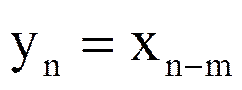
Последовательность y_n представляет собой сдвинутую (задержанную) на m отсчетов последовательность x_n

Тогда Z-преобразование Y(z) последовательности y_n выражается через Z-преобразование X(z) последовательности x_n следующим образом

.

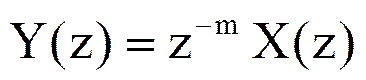Таким образом, Z-преобразование последовательности, сдвинутой относительно исходной на m отсчетов, равно Z-преобразованию исходной последовательности, умноженной на z ^–m.

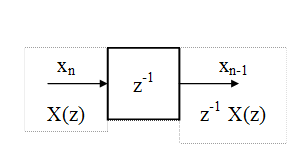
Пример №1

Выразите Z –преобразование Y(z) выходного сигнала y_n цифровой линии задержки через Z – преобразование X(z) входного сигнала x_n

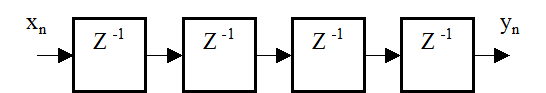
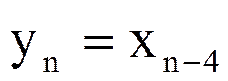
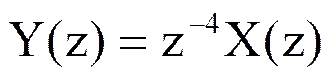
Пример №2

Выразите Z-преобразование сигнала y_n через Z-преобразование сигнала x_n, если

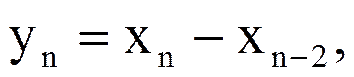
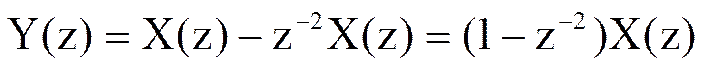
3.Дискретная свертка двух последовательностей. Дискретной сверткой двух последовательностей x_n и h_n называется последовательность y_n, ,определяемая следующим соотношением

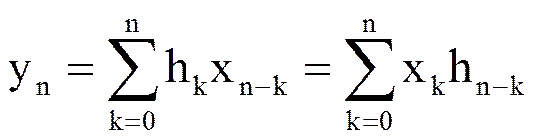
Z-преобразование Y(z) дискретной свертки двух последовательностей y_n равно произведению Z-преобразований H(z) и X(z) исходных последовательностей h_n и x_n

,

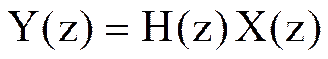где .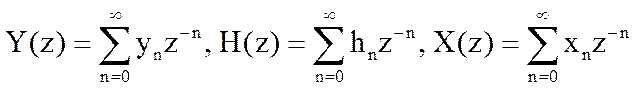

Пример

Определите Z-преобразование свертки y_n дискретных сигналов

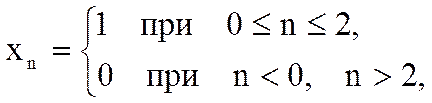
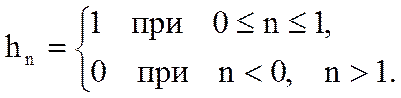
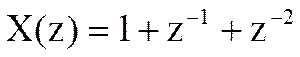
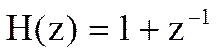
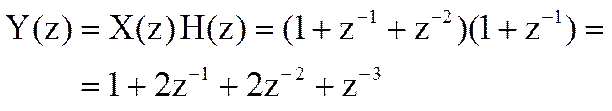
2.2. Импульсная характеристика цифрового фильтра. Понятие о рекурсивных и нерекурсивных цифровых фильтрах, БИХ- и КИХ-фильтрах

Цифровым фильтром называется линейная частотно-избирательная система, реализуемая на основе вычислительного устройства.

Если n-ый отсчет выходного сигнала фильтра y_n зависит только от отсчетов входного сигнала в данный и предшествующие моменты дискретного времени x_n, x_n-1 ..и т.д., то такой фильтр называется нерекурсивным.

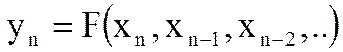
Если n-ый отсчет выходного сигнала фильтра y_n зависит не только от отсчетов входного сигнала в данный и предшествующие моменты дискретного времени x_n, x_n-1 ..и т.д., но и от отсчетов выходного сигнала в предшествующие моменты времени, то такой фильтр называется рекурсивным.

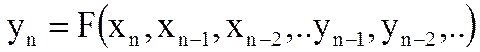
Импульсной характеристикойцифрового фильтра называется выходной сигнал фильтра при действии на его входе единичного отсчета и нулевых начальных условиях.

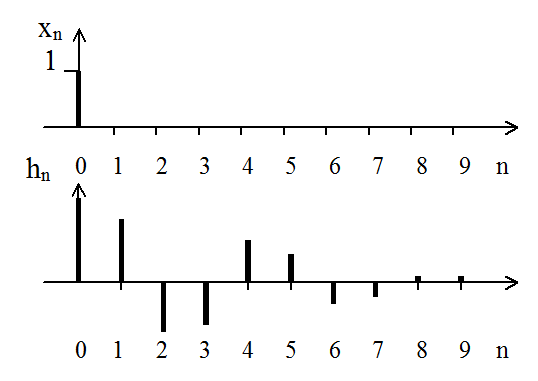
Фильтр с конечной импульсной характеристикой называется КИХ - фильтром (КИХ -конечная импульсная характеристика). Фильтр с бесконечной импульсной характеристикой называют БИХ - фильтром.

2.3. Определение выходного сигнала фильтра по входному сигналу и импульсной характеристике

Определение выходного сигнала цифрового фильтра по входному сигналу и импульсной характеристики основано на определении импульсной характеристики и принадлежности фильтра к линейным системам, для которых справедлив принцип суперпозиции.

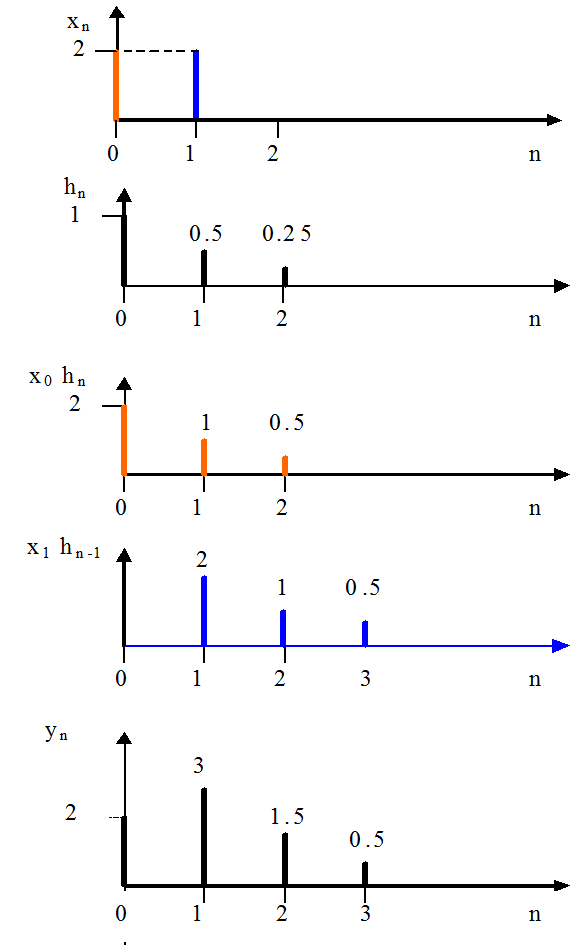
Так как фильтр линейная система, то при входном отсчете в x₀ раз больше единичного, выходной сигнал будет представлять собой импульсную характеристику, все отсчеты которой умножены на x₀, - x₀ h_n.

Определим реакцию фильтра на отсчет сигнала x₁ при x₀ =0. При x₁=1 выходной сигнал фильтра представлял бы собой импульсную характеристику, запаздывающую на один отсчет h_n-1. При отсчете x₁, отличном от единицы, реакцией фильтра будет запаздывающая на один отсчет импульсная характеристика, все отсчеты которой умножены на x₁, - x₁ h_n-1.

Согласно принципу суперпозиции полученные реакции суммируются.

В результате

,

, …..

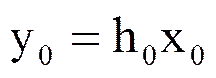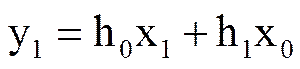В общем случае

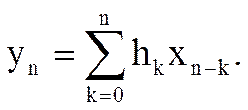(1)

Согласно последнему соотношению

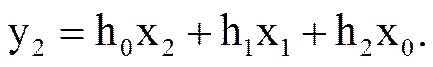
Однако в рассмотренном примере x₂ = 0, поэтому, как видно из рисунка,

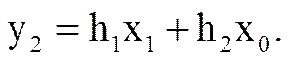
В общем случае

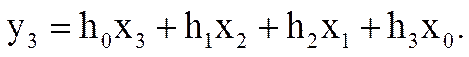
В данном примере x₂ = x₃ = 0, h₃ = 0, поэтому

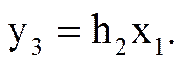
Соотношение (1) представляет собой дискретную свертку последовательностей x_n и h_n, т.е. выходной сигнал фильтра представляет собой дискретную свертку входного сигнала и импульсной характеристики фильтра.

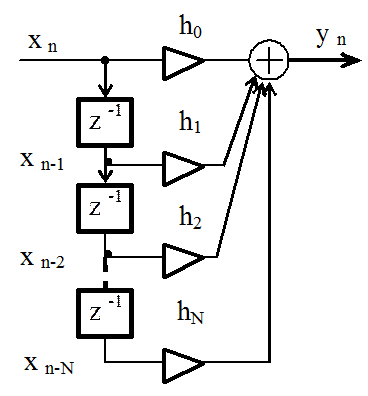
2.4. Системная функция цифрового фильтра. Формы программной реализации фильтра