Декартово произведение множеств
Декартовым произведением множеств А и В называют множество всех пар, первая компонента которых принадлежит множеству А, вторая - множеству В.
А × В = {(x; y) | x∈A и y∈B}
пример: Проверить справедливость равенства А×С=(А× (С \ В)) È
È (А× (С Ç В)), если А={1,2}, В={2,3}, С={1,3}.
решение:
1) А×С = {1,2}×{1,3}={(1,1);(1,3);(2,1);(2,3)}.
2) С \ В = {1,3}\{2,3}={1};
3) А× (С \ В) = {1,2}×{1}={(1,1);(2,1)};
4) С Ç В = {1,3}Ç{2,3}={3};
5) А× (С Ç В) = {1,2}×{3}={(1,3);(2,3)};
6) 3È5 = {(1,1);(2,1)} È {(1,3);(2,3)}={(1,1);(1,3);(2,1);(2,3)}.
Равенство справедливо.
Наглядно представить декартово произведение можно с помощью графа или таблицы (в случае, если множества конечны и содержат небольшое число элементов), а также координатной плоскости.
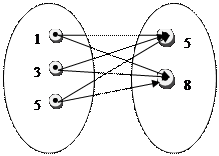
пример: А={1,3,5} и В={5,8} найти А×В
с помощью графа:
 |
табличный способ:
| А | В | |
| (1,5) | (1,8) | |
| (3,5) | (3,5) | |
| (5,5) | (5,8) |
на координатной плоскости:
 у
у
 |


 8 * * *
8 * * *
 5 * * *
5 * * *
0 1 3 5 х
Так как нам надо найти А×В, то элементы множества А отметим на оси Ох, а элементы множества В на оси Оу. Звездочками обозначены координаты декартова произведения.
Представление декартова произведения множеств с помощью координатной плоскости целесообразно использовать в случаях, когда хотя бы одно из множеств является бесконечным.
Дата добавления: 2020-02-05; просмотров: 1091;











