Охлаждение (нагревание) тел конечных размеров
а) Охлаждение параллелепипеда
Рассмотрим охлаждение параллелепипеда в среде с постоянной температурой и с постоянным коэффициентом теплоотдачи a на всех его гранях. В начальный момент времени (t=0) все точки параллелепипеда имеют одинаковую температуру t0. Параллелепипед с размерами 2dx´2dy´2dz является однородным и изотропным. Требуется найти распределение температуры в параллелепипеде для любого момента времени, а также среднюю температуру для определения количества отведенной (подведенной) теплоты.
Поместим начало координат в центре параллелепипеда. При этом дифференциальное уравнение запишется следующим образом:
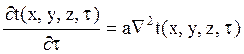 (19)
(19)
Параллелепипеды, цилиндры конечных размеров, и прямоугольные стержни можно рассматривать как тела, образованные пересечением соответственно трех взаимно перпендикулярных неограниченных пластин конечной толщины, цилиндра и пластины и двух пластин.
Можно доказать, что решение таких задач представляется произведением безразмерных температур для тел неограниченных размеров, в результате пересечения которых образовалось рассматриваемое тело.
Таким образом, для параллелепипеда решение можно представить в виде:
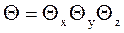 (20)
(20)
где
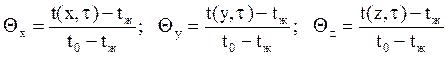
Общее решение (20) в развернутом виде запишется следующим образом:
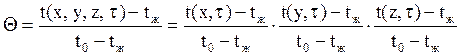 (20a)
(20a)
Приведенное решение удовлетворяет как дифференциальному уравнению, так и граничным условиям.
Таким образом, решение задачи для рассматриваемого тела свелось к решению задачи для безграничной пластины конечной толщины. Уравнение (20) можно представить в виде:
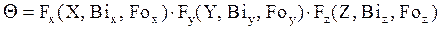 (20б)
(20б)
Множители в уравнении (20) вычисляются по формуле (12).
Рассмотренный метод известен в теории теплопроводности под названием теоремы о перемножении решений. Полученное решение справедливо и для нахождения средней температуры.
Средняя безразмерная температура параллелепипеда выражается следующим образом:
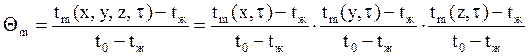
или
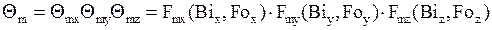 (21)
(21)
В уравнении (21) множители находятся по формуле (18).
Следует отметить, что теорема о перемножении решений справедлива и в более общем случае, когда коэффициенты теплопроводности различны для различных направлений, коэффициенты теплоотдачи на гранях разные.
б) Охлаждение длинного прямоугольного стержня.
Такое тело можно рассматривать как результат пересечения двух пластин толщиной 2dx и 2dy.
Безразмерное температурное поле для поставленной задачи есть
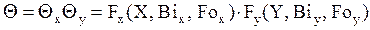
Множители в последнем уравнении определяют по формуле (12).
в) Охлаждение цилиндра конечной длины.
Конечный цилиндр можно рассматривать как результат пересечения безграничных цилиндра диаметром 2r и пластины толщиной 2dz; следовательно и безразмерную температуру для такого тела можно записать как
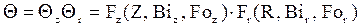
В последнем уравнении в качестве определяющих линейных размеров берется половина высоты цилиндра dz и радиус r.
Дата добавления: 2018-11-26; просмотров: 1453;











