Математическая формулировка задачи

Нестационарная теплопроводность

Постановка задачи

Пусть теплофизические характеристики постоянны (l, с, r) и заданы граничные условия третьего рода, которые наиболее часто встречаются на практике. Задача формулируется следующим образом:

Плоская неограниченная пластина толщиной d, имеющая во всех точках одинаковую начальную температуру t_н в момент времени t=0 помещается в среду, температура которой t_ж<t_н. Температура среды во время охлаждения поддерживается постоянной. Охлаждение пластины происходит через обе ее поверхности с одинаковой интенсивностью путем теплоотдачи. Коэффициент теплоотдачи a известен и не меняется во времени.

Требуется найти температурное поле пластины в произвольный момент

времени t>0.

Математическая формулировка задачи

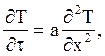(1)

где x меняется в пределах 0£х£d/2 (Начало координат в середине пластины и рассматривается процесс только в одной ее половине)

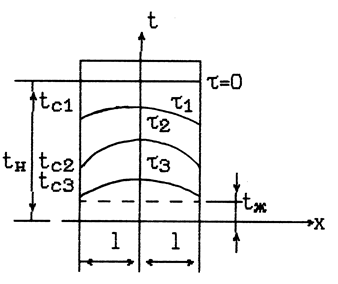Рис. 1.

Краевые условия:

1. Начальные условия.

t=0; 0£х£l; t=t_н; l=d/2.

2. Граничные условия.

а) при х=0 и t>0, (¶t/¶x)₀=0, так как при симметричном охлаждении в середине пластины в любой момент времени температура будет максимальной (рис.1),

б) при х=l и t>0, .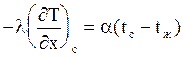

3. Выполним операцию приведения уравнения (1) к безразмерной форме. Для чего заменим t избыточной температурой n=t-t_ж. Так как dn=dt, то уравнение (1) примет вид:

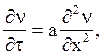(2)

при t=0; 0£х£l; n=n_н=t_н-t_ж,

при х=0 и t>0 (¶n/¶x)₀=0,

при х=l и t>0 , где n_c=t_с-t_ж.

Далее вместо избыточной температуры введем безразмерную избыточную температуру Q=n/n_н=(t-t_ж)/(t_н-t_ж), а вместо координаты х - безразмерную координату Х=х/l.

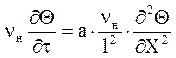
откуда после сокращения и преобразования получим:

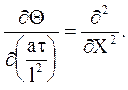
В данной форме дифференциальное уравнение безразмерно. Комплекс at/l²=Fo - критерий Фурье, который можно трактовать как безразмерное время.

Окончательно дифференциальное уравнение теплопроводности в безразмерной записи получается в более простом виде:

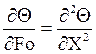(3)

Начальное условие при Fo=0; Q_н=1,

граничное условие при X=0, (¶Q/¶X)₀=0, (*)

при X=1, (¶Q/¶X)_c=-Bi×Q_c,

где Q_c= n_c/n_н - безразмерная температура стенки.

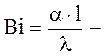критерий Био.

Физический смысл критерия Био состоит в том, что его величина характеризует соотношение интенсивностей отвода теплоты в процессе теплоотдачи и подвода теплоты из внутренних слоев тела к поверхности за счет теплопроводности.