Решение задачи методом разделения переменных

Этот метод был предложен Фурье, который предложил искомую функцию температурного поля представить в виде произведения двух функций, одна из которых j(t) зависит только от температуры, а другая y(x) – только от координаты.

То есть t(t, x) = j(t)×y(x) или в безразмерной форме

Q=j(Fo)×y(X).

Указанное решение должно удовлетворять уравнению (3). Если это так, то частная производная произведения j(Fo)×y(X) по Fo должна быть равна второй частной производной этого же произведения по Х, откуда:

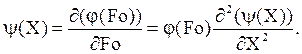
В последнем уравнении легко разделяются переменные:

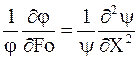, (4)

Равенство (4) должно выполняться при любых значениях аргументов, что возможно, если каждая его часть равна одной и той-же постоянной величине.

Обозначим эту величину -m²=const.

Таким образом:

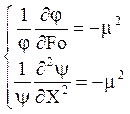, (5)

Решение будет иметь вид:

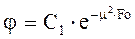
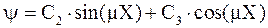
Таким образом, искомая функция температуры будет иметь вид:

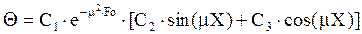(6)

Значения постоянных находят из начальных и граничных условий (*)

Найдем 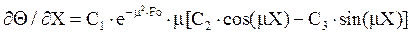(7)

При X=0, ¶Q/¶X=0, C₂=0. Это означает, что частное решение y=C₂×sin(mX) должно быть отброшено, так как оно не удовлетворяет граничному условию. Поэтому вместо уравнений (6 и 7) получаем:

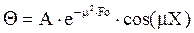, (8)

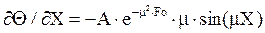, (9)

где A = C₁×C₂.

В соответствии с условиями (*) находим:

,

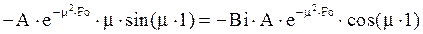откуда 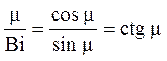. (10)

Уравнение (10) называют характеристическим уравнением и из него находят корни m.

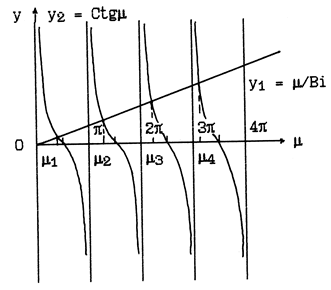Рис 1.

Покажем графоаналитический метод решения (рис.1).

m₁<m₂<m₃…<m_n<…- бесконечный ряд

Каждому значению корня m_n будет соответствовать свое частное распределение температуры.

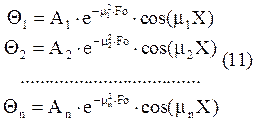
Окончательное решение задачи в безразмерной форме представляется выражением:

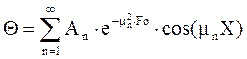, (12)

где 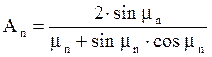, (13)

m_n - корни характеристического уравнения (10), зависящие от критерия Bi, а коэффициенты A_n являются функциями от m_n. Значения A_n, m_n приводятся в таблицах в функции от критерия Био.