Работа и теплота как функции процесса

Предположим, что имеем цилиндр с поршнем. В запоршневом пространстве находится рабочее тело. К рабочему телу подводится тепло в результате чего рабочее тело может расшириться.

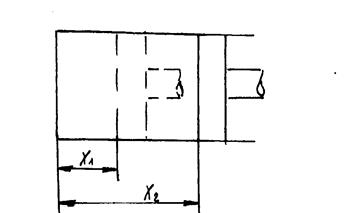Сила P действующая со стороны рабочего тела на поршень равна

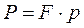
где F – площадь поршня.

Рис. 2.2. К определению работы совершаемой рабочим телом.

При бесконечно малом перемещении поршня на расстояние dx будет совершена элементарная работа dL

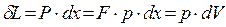(2.9)

где 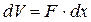- элементарное изменение объёма рабочего тела.

Тогда полная работа при перемещении поршня определится выражением

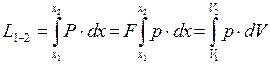(2.10)

Как видно из выражения (2.10) работа, совершаемая рабочим телом, зависит от характера изменения давления в процессе движения поршня.

Разделив выражения (2.9) и (2.10) на массу рабочего тела G , получим выражение для удельной работы

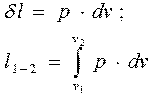
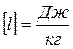(2.11)

Сопоставляя выражение (2.11) и диаграмму (а) на рис.2.1 видим, что работа графически выражается площадью над кривой процесса в ( - ) диаграмме.

Используя выражение (2.6) и (2.7) можем записать

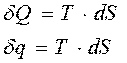(2.12)

Интегрируя последние выражения от начального состояния (1) до конечного состояния (2) получим соответственно:

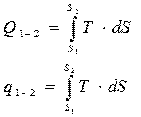(2.13)

Как видно из выражения (2.13) полное и удельное тепло подведённое (отведённое) к рабочему телу зависит от вида функции T (S ), т.е. зависит от характера процесса.

Таким образом очевидно, что работа и тепло не являются функциями состояния, а являются функциями процесса.

Теплоёмкость.

Способность рабочих тел поглощать тепло характеризуется теплоёмкостью.

Теплоёмкость тела C численно равна количеству тепла, которое нужно подвести к рабочему телу, чтобы нагреть его на один градус.

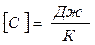
Удельная теплоёмкость численно равна количеству тепла, которое необходимо подвести к единице количества вещества, чтобы нагреть его на один градус.

В зависимости от выбора единицы измерения количество вещества различают:

- на массовую теплоёмкость

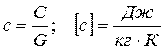
- на объёмную теплоёмкость

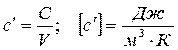
- на мольную теплоёмкость

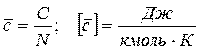
где N - количество молей вещества.

Используя соотношения между единицами измерения количества вещества, можно записать

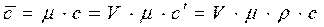
где m - молекулярная масса вещества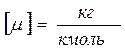

V_m - мольный объём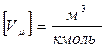

r - плотность вещества кг/м³ .

Теплоемкости газа в различных термодинамических процессах (расширение сжатие с подводом или отводом тепла) могут меняться в очень широких пределах. Особое значение в технической термодинамике занимают процессы при постоянном объёме V=const и постоянном давлении p=const и соответствующие им теплоёмкости:

- при постоянном объёме -

- при постоянном давлении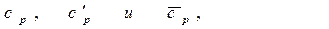

Теплоёмкости c_p и c_V связаны между собой известным уравнением Майера

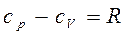(2.14)

т.е. величина c_p всегда больше величины c_V на величину работы, совершаемой газом при нагревании на 1° при p=const.

Для определения удельной теплоёмкости экспериментальным путём к определённому количеству газа массой G подводится определённое количество тепла Q, при этом газ нагревается от температуры t₁ до t₂. Удельная теплоёмкость определяется по зависимости

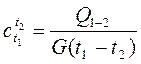(2.15)

Определённая таким образом теплоёмкость является средней в заданном диапазоне температур t₁ ¸ t₂.

Каждая из ранее рассматриваемых теплоёмкостей зависит от температуры, поэтому для определения истинного значения теплоёмкости, соответствующей данной температуре t, необходимо, чтобы при измерениях t₂®t₁ тогда истинная теплоёмкость определится выражением

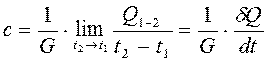(2.16)

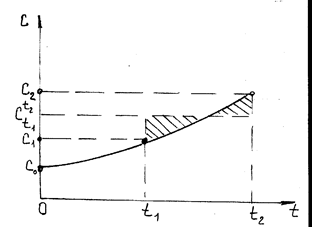
Характерный вид зависимости c(t) представлен на рис.2.3.

Обычно аналитическое выражение зависимости c(t) представляется в виде полиномиального ряда

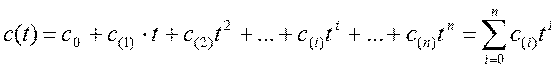
Значения c(t) для различных веществ приводятся в справочной литературе.

При известной зависимости c(t), количество тепла Q необходимое, что-бы нагреть массу рабочего тела G от температуры t₂ до температуры t₁, определится зависимостью

	Рис. 2.3. Характерная зависимость c(t)

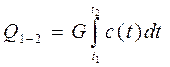(2.17)

или при нагревании I кг газа

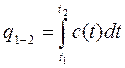(2.17.а)

Во многих термодинамических процессах температура рабочего тела меняется в довольно ограниченных пределах, при этом удельная теплоёмкость меняется незначительно. В таких случаях, для упрощения аналитических выкладок и сокращения расчётных процедур удельную теплоёмкость в заданном диапазоне температур t₁ ¸ t₂, полагают постоянной величиной, равной некоторому среднему значению.

Тогда, положив в (2.17) и (2.17.а) 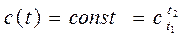получим

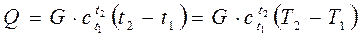(2.18)

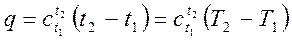(2.18.a)

Для нахождения 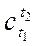по известной зависимости c(t) и заданному диапазону температур t₁ ¸ t₂, приравняем выражения (2.17) и (2.18) и найдём

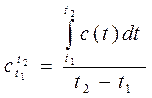
(2.19)

Для упрощения процедуры нахождения 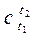в справочниках часто приводят значения средних теплоёмкостей от 0° С до отдельных значений – t_i. Такие данные представляют таблицей

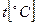
		t1	T2	. . . . . . .	ti	. . . . . . .	tn
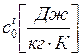
	C0			. . . . . . .		. . . . . . .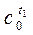

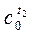
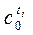
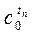
Для нахождения средней теплоёмкости в диапазоне t₁ ¸ t₂ вычислим количество тепла, которое необходимо подвести I кг газа, чтобы нагреть его от 0 °С до t₂ °С и от 0° до t₁ °С.

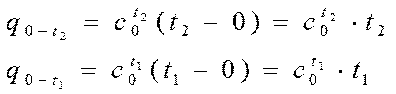
Очевидно, что количество тепла 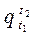, которое необходимо, чтобы нагреть 1 кг газа от t₁ °Сдо t₂ °С будет равно разности

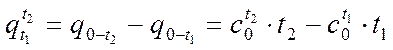(а)

Приравняв (2.18.а) и (а) найдём

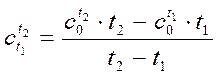(2.20)

* При анализе 2^ого закона термодинамики будет доказано, что S - является функцией состояния, т.е. dS - полный дифференциал.