ЕВОЛЬВЕНТНАЯ ЗУБЧАСТА ПЕРЕДАЧА

Коротке содержание:Эвольвентное зубчате колесо і його параметри. Товщина зуба колеса по колу довільного радіусу. Методи виготовлення эвольвентных зубчатих коліс. Поняття про початковий, початковий контурах, що проводять і проводять. Верстатне зачеплення. Основні розміри зубчатого колеса. Види зубчатих коліс.Підрізування і загострення колеса. Поняття про область існування зубчатого колеса. Евольвентная циліндрова зубчата передача і її параметри. Основні рівняння эвольвентного зачеплення.

Контрольні питання |Список додаткової літератури

Евольвентноє зубчате колесо і його параметри.

Евольвентним зубчатим колесом називають ланку зубчатого механізму, забезпечену замкнутою системою зубів. При проектуванні зубчатого колеса спочатку потрібно визначити його число зубів z, а потім визначити параметри зубів. Для цього потрібно довільне коло колеса ry розділити на z частин, кожна з яких називається окружним кроком py.

де my= py /p = dy / z - модуль зачеплення по колу довільного радіусу.

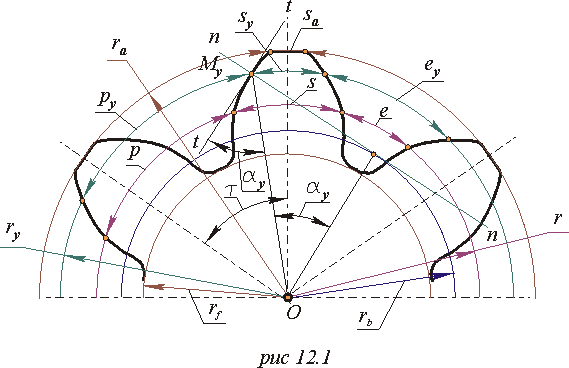
Модулем зачеплення називається лінійна величина в p разів менша окружного кроку або відношення кроку по будь-якому концентричному колу зубчатого колеса до p . Залежно від кола по якій визначений модуль розрізняють ділильний, основний, початковий. Для косозубых коліс ще і нормальний, торцевий і осьовий модулі. У ряді країн використовується величина зворотна модулю, яка називається питчем. Пітч (діаметральний) - число зубів колеса, що доводиться на дюйм діаметру. Виходячи з цього модуль можна визначити як число милиметров діаметру, що доводиться на один зуб. На колесі можна провести незліченне число кіл на кожній з яких буде свій модуль. Для обмеження цього числа Гостом введений стандартний ряд модулів. Стандартною модуль визначається по колу званому ділильному. Точнєєделітельной називається таке коло зубчатого колеса, на якому модуль і крок набувають стандартного значення. Окружним кроком або кроком називається відстань по дузі кола між однойменними точками профілів сусідніх зубів (під однойменними розуміються праві або ліві профілі зуба). Кутовий крок t - центральний кут відповідний дузі p - окружному кроку по ділильному колу.

Примітка: Згідно ГОСТ основні елементи зубчатого колеса позначаються по наступних правилах: лінійні величини - рядковими буквами латинського алфавіту, кутові - грецькими буками; встановлені індекси для величин :

по колах: ділильною - без індексу, вершин - а, западин - f , основна, - b , початкова, - w , нижніх точок активних профілів коліс - p , граничних крапок - l ;

по перетинах: нормальний перетин - n , торцевий перетин - t , осьовий перетин - x ;

що відносяться до зуборізного інструменту - 0 .

Для параметрів зубчатого колеса справедливі наступні співвідношення

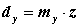- діаметр кола довільного радіусу

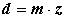- діаметр ділильного кола

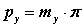- крок по колу довільного радіусу

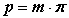- крок по ділильному колу

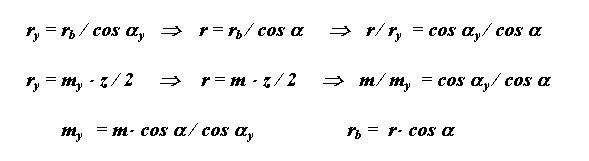
де а - кут профілю на ділильному колі

а у - кут профілю на колі довільного радіусу.

Кутом профілю називається гострий кут між дотичною до профілю в даної крапки і радіусом - вектором, проведеним в дану крапку з центру колеса.

Крок колеса ділиться на товщину зуба sy і ширину западини ey . Товщина зуба sy - відстань по дузі кола ry між різнойменними точками профілів зуба. Ширіна западини ey - відстань по дузі кола ry між різнойменними точками профілів сусідніх зубів.

На основному колі а b=> 0 і cos а b=> 1, тоді

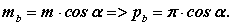
Залежно від співвідношення між товщиною зуба і шириною западини на ділильному колі зубчаті колеса діляться на:

нульові s = e = p * m / 2, D = 0;

позитивні s > e =>D > 0;

негативні s < e => D < 0;

де D - коефіцієнт зміни товщини зуба (відношення приросту товщини зуба до модуля). Тоді товщину зуба по ділильному колу можна записати

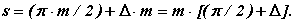
Детальніше познайомитися з основними визначеннями і розрахунковими залежностями можна в літературі [ 11.1 ] і в ГОСТ 16530-83.

Товщина зуба колеса по колу довільного радіусу.

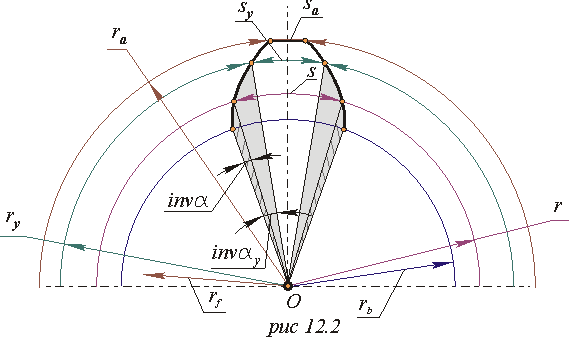
Товщина зуба по дузі ділильного кола

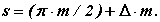
Кутова товщина зуба по колу довільного радіусу з схеми на мал. 12.2

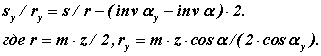
Підставляючи у формулу кутової товщини ці залежності, отримаємо

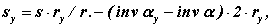
або

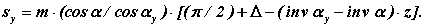
Методи виготовлення эвольвентных зубчатих коліс.

Існує безліч варіантів виготовлення зубчатих коліс. У їх основу покладені два принципово відмінних методу:

метод копіювання, при якому робочі кромки інструменту формою відповідають оброблюваній поверхні ( конгруентны їй, тобто заповнюють цю поверхню як відливання заповнює форму );

метод обгинання, при якому інструмент і заготівка за рахунок кінематичного ланцюга верстата виконують два рухи - різання і обгинання (під обгинанням розуміється такий відносний рух заготівки і інструменту, який відповідає верстатному зачепленню, тобто зачепленню інструменту і заготівки з необхідним законом зміни передавального відношення).

З варіантів виготовлення за способом копіювання можна відзначити:

Нарізування зубчатого колеса профільованою дисковою або пальцевою фрезою (проекція ріжучих кромок якої відповідає конфігурації западин). При цьому методі різання проводиться в наступному пасмочці: прорізається западина першого зуба, потім заготівка за допомогою ділильного пристрою (ділильної головки) повертається на кутовий крок і прорізається наступна западина. Операції повторюються поки не прорізатимуть всі западини. Продуктивність даного способу низька, точність і якість поверхні невисокі.

Відливання зубчатого колеса у форму. При цьому внутрішня поверхня ливарної форми конгруентна зовнішньої поверхні зубчатого колеса. Продуктивність і точність методу висока, проте при цьому не можна отримати високої міцності і твердості зубів.

З варіантів виготовлення за способом обгинання найбільше розповсюдження мають:

Обробка на зубофрезерных або зубодолбежных верстатах черв'ячними фрезами або долбяками. Продуктивність достатньо висока, точність виготовлення і чистота поверхонь середня. Можна обробляти колеса з матеріалів з невисокою твердістю поверхні.

Накатка зубів за допомогою спеціального профільованого інструменту. Забезпечує високу продуктивність і хорошу чистоту поверхні. Застосовується для пластичних матеріалів, зазвичай на етапах чорнової обробки. Недолік методу утворення поверхневого шару, що наклепує, який після закінчення обробки змінює свої розміри.

Обробка на зубошлифовальных верстатах дисковими кругами. Застосовуємося як остаточна операція після зубонарезания (або накатки зубів) і термічної обробки. Забезпечує високу точність і чистоту поверхні. Застосовується для матеріалів з високою поверхневою міцністю.

Поняття про початковий, початковий контурах, що проводять і проводять .

Для скорочення номенклатури ріжучого інструменту стандарт встановлює нормативний ряд модулів і певні співвідношення між розмірами елементів зуба. Ці співвідношення визначаються:

для зубчатих коліс визначаються параметрами початкової рейки через параметри її нормального перетину - початковий контур;

для зубчатого інструменту визначаються параметрами початкової рейки, що проводить, через параметри її нормального перетину - початковий контур, що проводить.

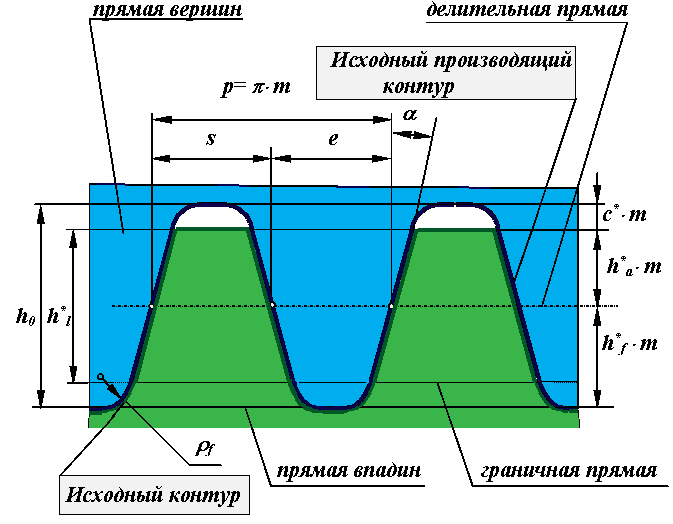
Рис 12.3

По ГОСТ 13755-81 значення параметрів початкового контура мають бути наступними:

кут головного профілю а = 20° ;

коефіцієнт висоти зуба h*a = 1 ;

коефіцієнт висоти ніжки h*f = 1.25 ;

коефіцієнт граничної висоти h*l = 2 ;

коефіцієнт радіусу кривизни перехідної кривої r *f =с */(1-sina )= 0.38 ;

коефіцієнт радіального зазору в парі початкових контурів з * = 0.25.

Початковий контур, що проводить, відрізняється від початкового висотою зуба h0 = 2.5m.

Початковий і такий, що початковий проводить контури утворюють між собою конруентную пару (мал. 12.3), тобто один заповнює інший як відливання заповнює заготівку (з радіальним зазором з *Чm у зоні прямої вершин зуба початкової рейки). Принципова відмінність цих контурів в тому, що початковий контур покладений в основу стандартизації зубчатих коліс, а що початковий проводить - в основу стандартизації зуборізного інструменту. Обидва ці контура необхідно відрізняти від контура, що проводить, - проекції ріжучих кромок інструменту на плоскість перпендикулярну осі заготівки.

Верстатне зачеплення.

Верстатним зачепленням називається зачеплення, утворене заготівкою колеса і інструментом, при виготовленні зубчатого колеса на зубообрабатывающем устаткуванні за способом обкату. Схема верстатного зачеплення колеса і інструменту з контуром, що проводить, співпадаючим з початковим контуром, що проводить, зображена на мал. 12.4.

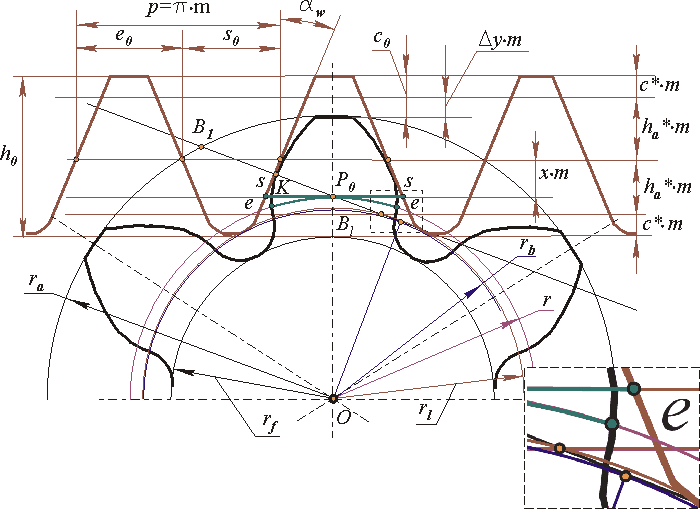
Рис 12.4

Лінія верстатного зачеплення - геометричне місце точок контакту эвольвентной частини профілю інструменту і эвольвентной частини профілю зуба в нерухомій системі координат.

Зсув початкового контура x*m , що проводить, - найкоротша відстань між ділильним колом заготівки і ділильної прямої початкового контура, що проводить.

Зрівняльний зсув D y*m - умовна розрахункова величина, введена в розрахунок геометрія зачеплення з метою забезпечення стандартного радіального зазору в зачепленні (величина, що виражає в долях модуля зменшення радіусу кіл вершин коліс, необхідне для забезпечення стандартної величини радіального зазору).

Коло граничних точок rl - коло що проходить через точки сполучення эвольвентной частини профілю зуба з перехідною кривою.

Основні розміри зубчатого колеса.

Визначимо основні розміри эвольвентного зубчатого колеса, використовуючи схему верстатного зачеплення (мал. 12.4).

Радіус кола вершин

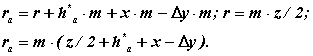
Висота зуба

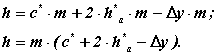
Радіус кола западин

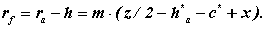
Товщина зуба по ділильному колу.

Оскільки стночно-начальная пряма перекочується в процесі обгинання по ділильному колу без ковзання, то дуга s-s по ділильному колу колеса дорівнює ширині западини e-e по верстатно-початковій прямій інструменту. Тоді, з урахуванням схеми на мал. 12.5, можна записати

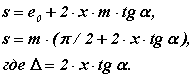
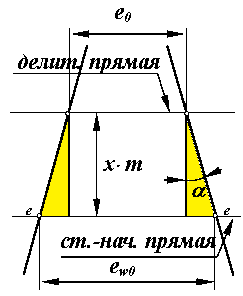
Мал. 12.5

Види зубчатих коліс (Класифікація за величиною зсуву).

Залежно від розташування початкового контура, що проводить, щодо заготівки зубчатого колеса, зубчаті колеса діляться на нульових або без зсуву, позитивних або з позитивним зсувом, негативних або з негативним зсувом.

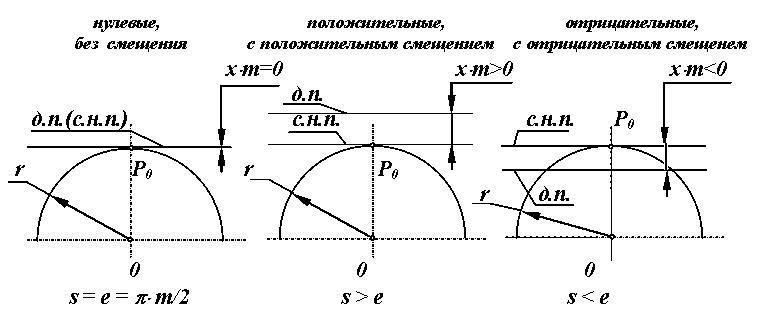
Мал. 12.6

Підрізування і загострення зубчатого колеса.

Якщо при нарізуванні зубчатого колеса збільшувати зсув, то основне і ділильне коло не змінюють свого розміру, а кола вершин і западин збільшуються. При цьому ділянка евольвенти, яка використовується для профілю зуба, збільшує свій радіус кривизни і профільний кут. Товщина зуба по ділильному колу збільшується, а по колу вершин зменшується.

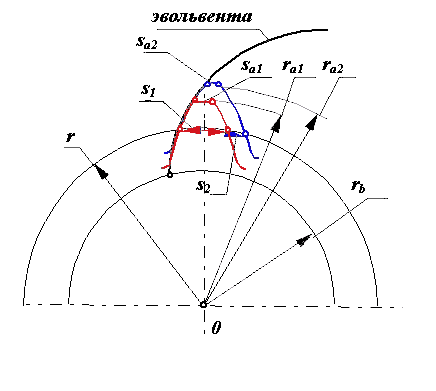
Мал. 12.7

На мал. 12.7 зображені два эвольвентных зуба для яких

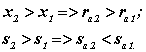
Для термобработанных зубчатих коліс з високою поверхневою міцністю зуба загострення вершини зуба є небажаним. Термообробка зубів (азотирова-ние, цементація, ціанування), що забезпечує высо Мал. 12.7 кую поверхневу міцність і твердість зубів при збереженні в'язкою серцевины, здійснюється за рахунок насичення поверхневих шарів вуглецем. Вершини зубів, як виступаючі елементи колеса, насищаються вуглецем більше. Тому після гарту вони стають твердішими і крихкішими. У загострених зубів з'являється схильність до сколювання зубів на вершинах. Тому рекомендується при виготовленні не допускати товщини зубів менших деяких допустимих значень. Тобто за загострений вважається зуб у якого

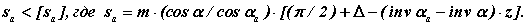
При цьому зручніше користуватися відносними величинами [sa /m ]. Зазвичай набувають наступних допустимих значень

поліпшення, нормалізація [sa /m ] = 0.2;

ціанування, азотування [sa /m ] = 0.25...0.3;

цементація [sa /m ] = 0.35...0.4.

Підрізування эвольвентных зубів у верстатному зачепленні

В процесі формування эвольвентного зуба за способом обгинання, залежно від взаємного розташування інструменту і заготівки можливе те, що зрізає эвольвентной частини профілю зуба тією частиною профілю інструменту, яка формує перехідну криву. Умова при якому це можливо визначається з схеми верстатного зачеплення. Ділянка лінії зачеплення, відповідна эвольвентному зачепленню визначається відрізком B1. де точка Bl визначається перетином лінії верстатного зачеплення і прямої граничних точок інструменту. Якщо точка Bl розташовується нижче (див. рис.12.8) за точку N , то виникає підрізування зуба. Умова при якому немає підрізування можна записати так

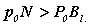
З D P0N0

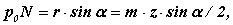
а з D P0BlF

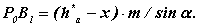
Тоді

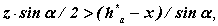
при x=0

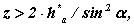
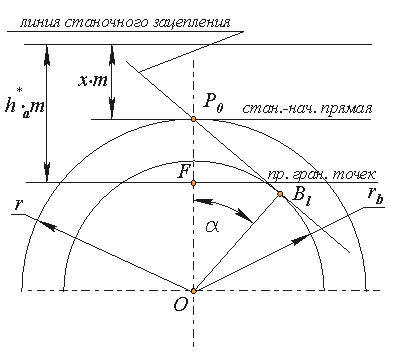
Мал. 12.8

Мал. 12.8 звідки

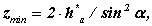
де zmin - мінімальне число зубів нульового колеса нарізуване без підрізування.

Уникнути підрізування колеса можна якщо збільшити зсув інструмент так, щоб точка Bl виявилася б вищою за точку N або збіглася з нею. Тоді зсув інструменту при якому не буде підрізування

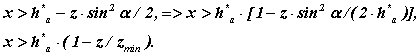
У граничному випадку, коли точка Bl збігається з точкою N

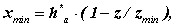
де xmin - мінімальний зсув інструменту при якому немає підрізування.

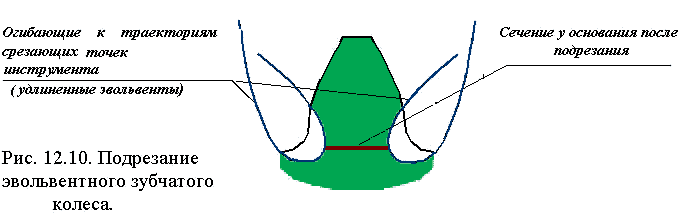
Мал. 12.10.

Поняття про область існування зубчатого колеса.

Параметри в зубчатих передачах зручно розділяти на параметри зубчатого колеса і параметри зубчатої передачі. Параметри зубчатого колеса характеризують дане зубчате колесо і, як складова частина, входять в параметри зубчатої передачі, утвореної цим колесом з іншим парним йому колесом. До параметрів зубчатого колеса відносяться: число зубів, модуль, параметри початкового контура інструменту, яким воно оброблялося і коефіцієнт зсуву. Як зазначено вище, на вибір цих параметрів накладаються обмеження по загостренню і підрізуванню зуба. Тому можна ввести поняття області існування зубчатого колеса - діапазону коефіцієнтів зсуву при яких не буде підрізування і загострення. На мал. 12.11 показаний приклад такої області існування.

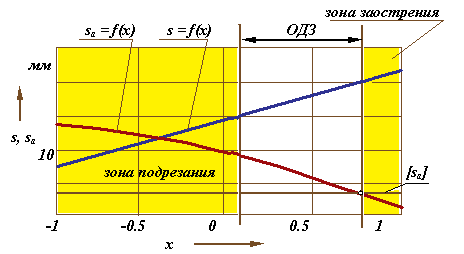
Мал. 12.11

Циліндрова эвольвентная зубчата передача.

Два зубчаті колеса з однаковим модулем і з числами зубів відповідними заданому передавальному відношенню утворюють зубчату передачу або простий зубчатий механізм. У цьому трехзвенном механізмі зубчаті колеса утворюють між собою вищу пару, а із стійкою нижчі пари. Зубчата передача, окрім параметрів створюючих її коліс, має і власні параметри: кут зачеплення а w, міжосьова відстань aw, сприйманий зсув y*m і зрівняльний зсув D y*m . Передавальне відношення механізму u12, числа зубів коліс z1 і z2, початкові кола rw1 і rw2(або центроиды) і міжосьова відстань aw зв'язані між собою наступними співвідношеннями ( див. основну теорему зачеплення і розділ по кінематиці зубчатої передачі):

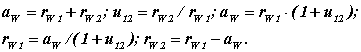
Зобразимо схему зачеплення эвольвентной зубчатої передачі (рис.12.12).

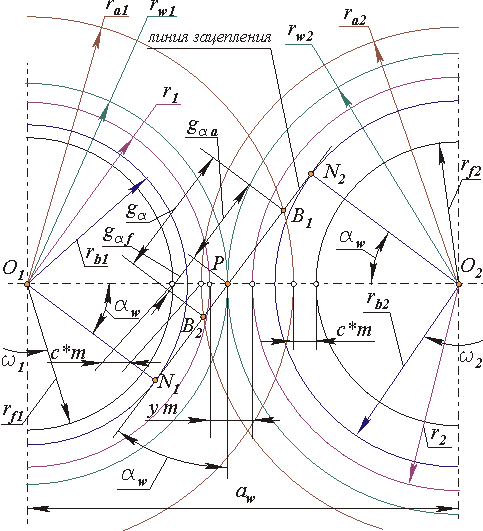
Мал. 12.12

Основні рівняння эвольвентного зачеплення.

1. Кут зачеплення а w

Оскільки перекочування початкових кіл один по одному відбувається без ковзання, то

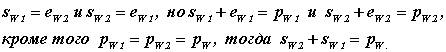s

Товщину зуба по початковому колу можна записати, використовуючи формулу для товщини зуба по колу довільного радіусу

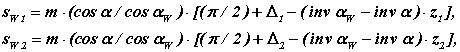
а крок по початковому колу рівний

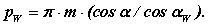
Поставляючи ці вирази у формулу для кроку по початковому колу, отримаємо

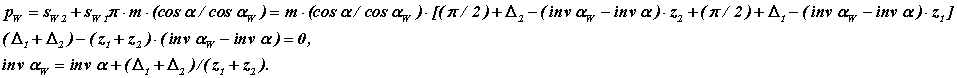
2. Міжосьова відстань aw

З схеми эвольвентного зачеплення (рис.12.12) можна записати

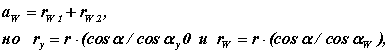
після підстановки, отримаємо

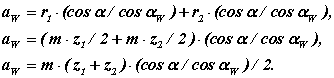
3. Сприйманий зсув y* m

З схеми эвольвентного зачеплення (рис.12.12) можна записати

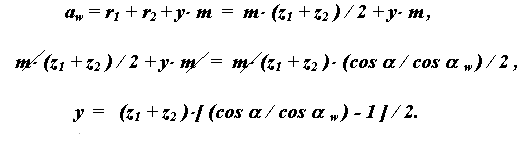
4. Зрівняльний зсув D y* m

З мал. 12.12

звідки

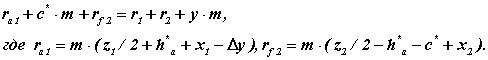
Підставимо ці вирази

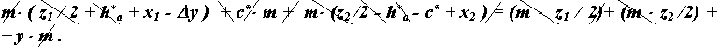
і, після перетворень, отримаємо

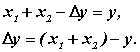
Контрольні питання до лекції 12

1. Що називається зубчатим колесом?(стр.1)

2. Дайте визначення модуля зачеплення .(стр.1)

3. Дайте визначення окружного і кутового кроку эвольвентного зачеплення (стр.2)

4. Запишіть формулу для товщини зуба по колу довільного радіусу (стр.3)

5. Які методи виготовлення эвольвентных зубчатих коліс Ви знаєте ?(стр.4)

6. У чому полягає суть виготовлення эвольвентных коліс методом обгинання?(стр.4-5)

7. Виведіть основні розміри зубчатого колеса (ra, s,h), використовуючи схему верстатного зачеплення (стр.7)

8. Запишіть умову відсутності підрізування у верстатному зачепленні (стр.9)

9. Що таке x min ? Виведіть формулу для визначення x min (стр.10)

10. Запишіть формулу для визначення кута зачеплення эвольвентной зубчатої передачі (стр.11)

Література до лекції 12.

В.А.Гавріленко . Зубчаті передачі в машинобудуванні (Теорія эвольвентных зубчатих передач). М.: Машгиз - 1962, 530 стор., илл.

Ф.Л.Літвін Теорія зубчатих зачеплень. Видавництво 2-е, перераб. і доп. М.: - Наука - 1968, 584 стор., илл.